Rectangular Prism|Definition & Meaning

Real World Applications 

Rectangular prisms are used in many real-world applications. Here are a few examples.

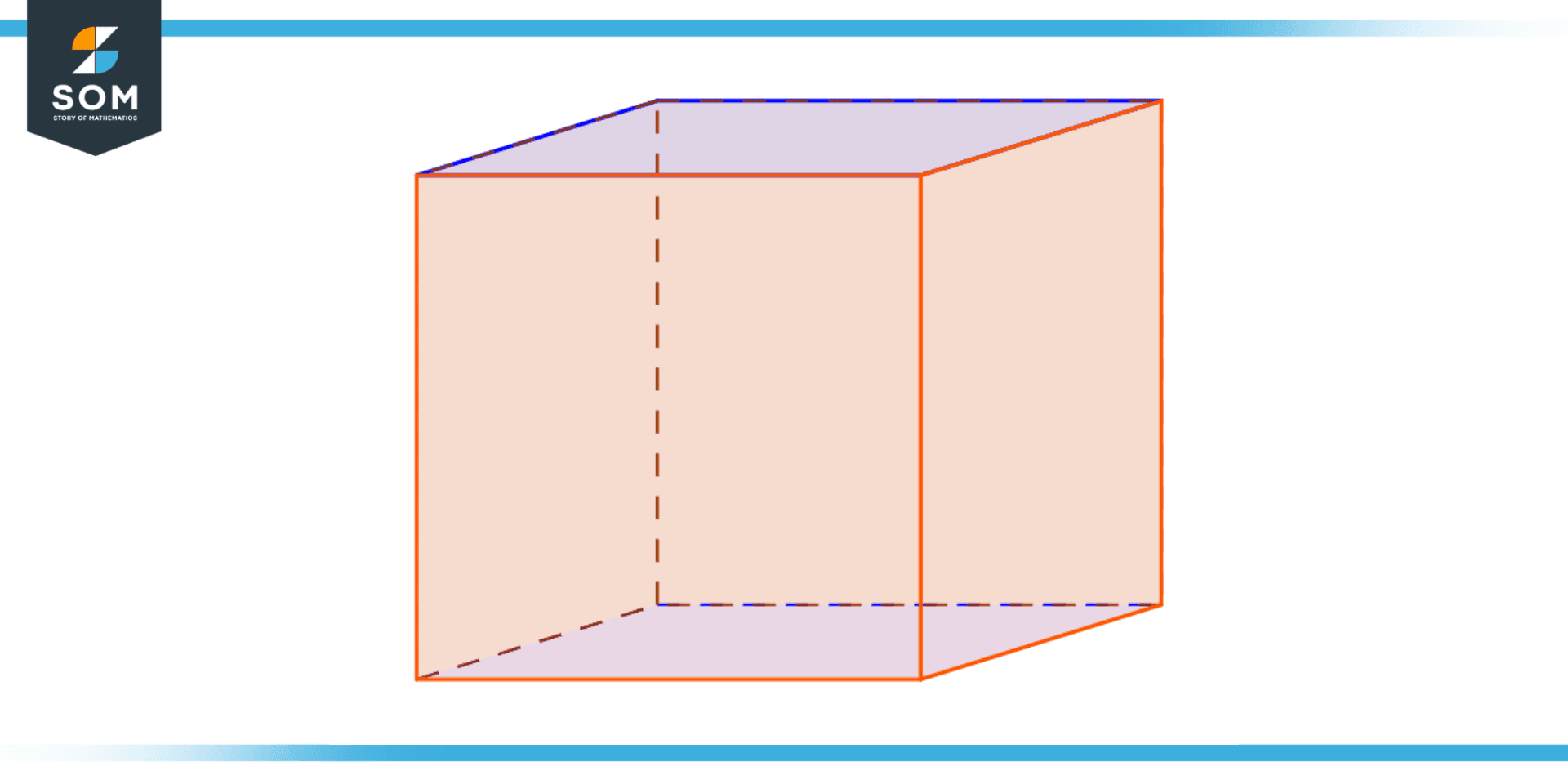
Figure 1 – Illustration of rectangular prism used in various applications in daily life

1. Boxes: Many commonplace things come packaged in rectangular prisms, including cereal boxes, shoe boxes, and gift boxes.
2. Buildings: A rectangular prism can roughly represent the shape of many different types of structures, including homes and office buildings.
3. Rectangular prisms are frequently used as storage and transportation containers. Bins, barrels, and shipping containers are a few examples.
4. Furniture: The rectangular prism shape is the basis for many items of furniture, including tables, workstations, and bookshelves.
5. Packaging: Many goods come in rectangular prism-shaped containers, such as milk cartons, and soda cans.
6. Geometry: Rectangular prisms are used to teach ideas like volume and surface area in geometry.

The Volume of Rectangular Prism

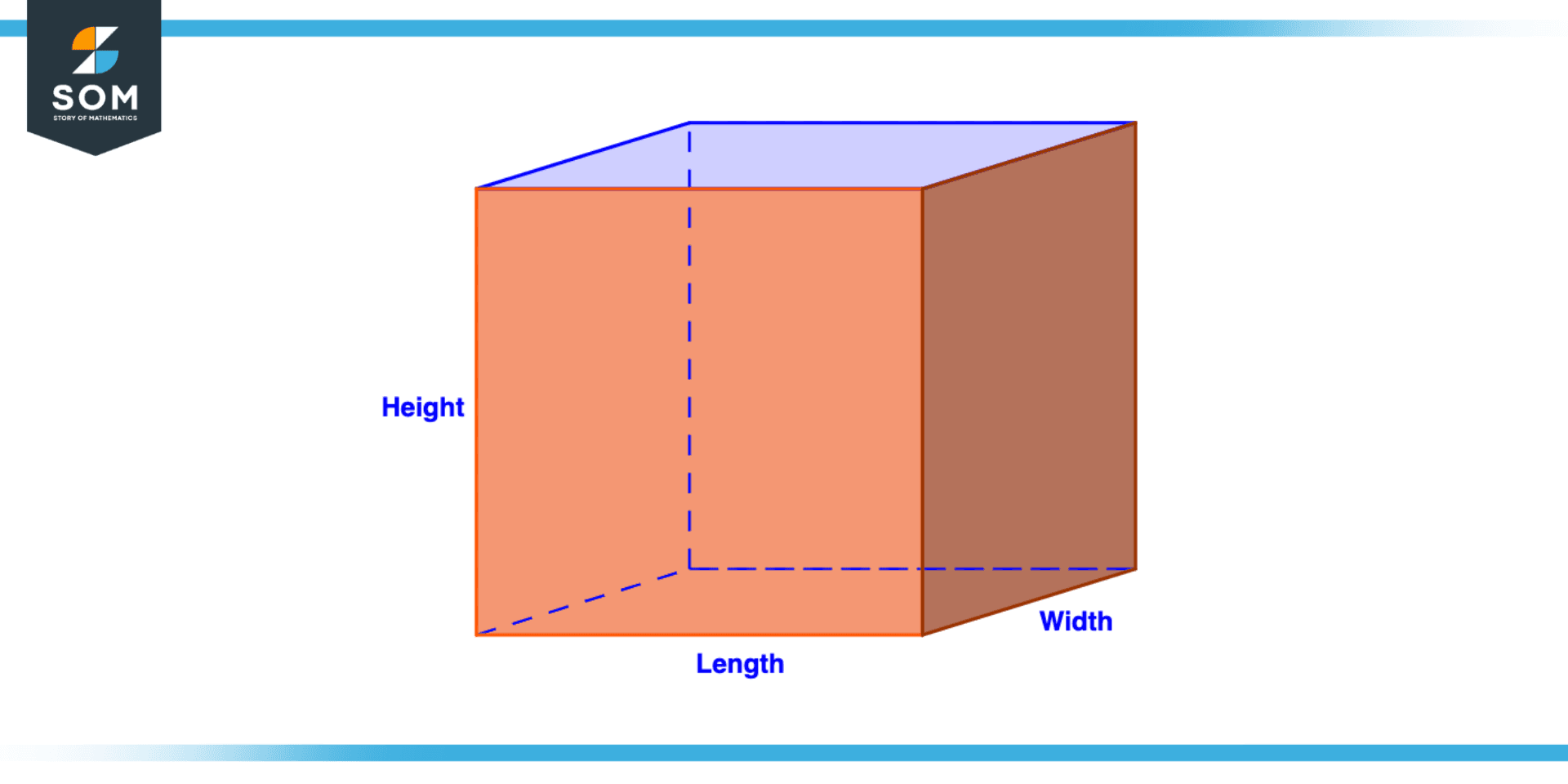
Figure 2 – Volume of Rectangular Prism

The amount of space a rectangular prism takes up is measured by its volume. It serves as a gauge for the capacity of the rectangular prism. It is calculated by multiplying the rectangular prism’s length, width, and height.

Volume = L x W x H

Here, V, L, W, and H are (respectively) the volume, length, width, and height of the rectangular prism.

Surface Area of Rectangular Prism

For a rectangular prism, the surface area is the total area of all of its faces. It is the sum of the areas of the six rectangular faces of the prism.

Surface Area = 2LW + 2LH + 2WH

Here, SA, L, W, and H are (respectively) the surface area, length, width, and height of the rectangular prism.

Properties of Rectangular Prism

Following are some important properties of a rectangular prism:

1. It has six rectangular faces, all of which are present.
2. The intersection points of the edges, or vertices, are eight.
3. It has a total of 12 straight edges.
4. It features three parallel pairs of faces on each side.
5. It features three opposed yet congruent sets of faces (the same size and shape).
6. A rectangular prism’s opposing faces are parallel to one another as well.
7. A rectangular prism has a length, breadth, and height that are all perpendicular to one another.
8. A rectangular prism’s volume is determined by multiplying its length by its width by its height.
9. A rectangular prism’s surface area is equal to the sum of all of its faces surface areas.
10. A rectangular prism contains depth in addition to length and width because it is a three-dimensional shape.

Right Rectangular Prism vs. Oblique Rectangular Prism

A right rectangular prism is a particular kind of rectangular prism that has right angles at each of its vertices and faces that are all perpendicular to one another. On the other hand, the faces of an oblique rectangular prism are not parallel to one another.

Here are some other distinctions between right and oblique rectangular prisms.

1. Shape: A right rectangular prism has straight edges, and right angles at all four corners, and is a regular shape. An irregular shape, an oblique rectangular prism has edges that aren’t always straight and corners that aren’t always at right angles.
2. Dimensions: A right rectangular prism has length, breadth, and height that are all perpendicular to one another. An oblique rectangular prism’s dimensions are not always parallel to one another.
3. Volume: The formula V = Length x Width x Height can be used to determine the volume of a right rectangular prism. L stands for length, w for width, and h for height. This formula cannot be used to determine the volume of an oblique rectangular prism because the dimensions are not parallel.
4. Surface area: The formula SA = 2lw + 2lh + 2wh can be used to get the surface area of a right rectangular prism. L stands for length, w for width, and h for height. This formula cannot be used to get the surface area of an oblique rectangular prism because the dimensions are not parallel.

Rectangular Prism as a Lunch Box

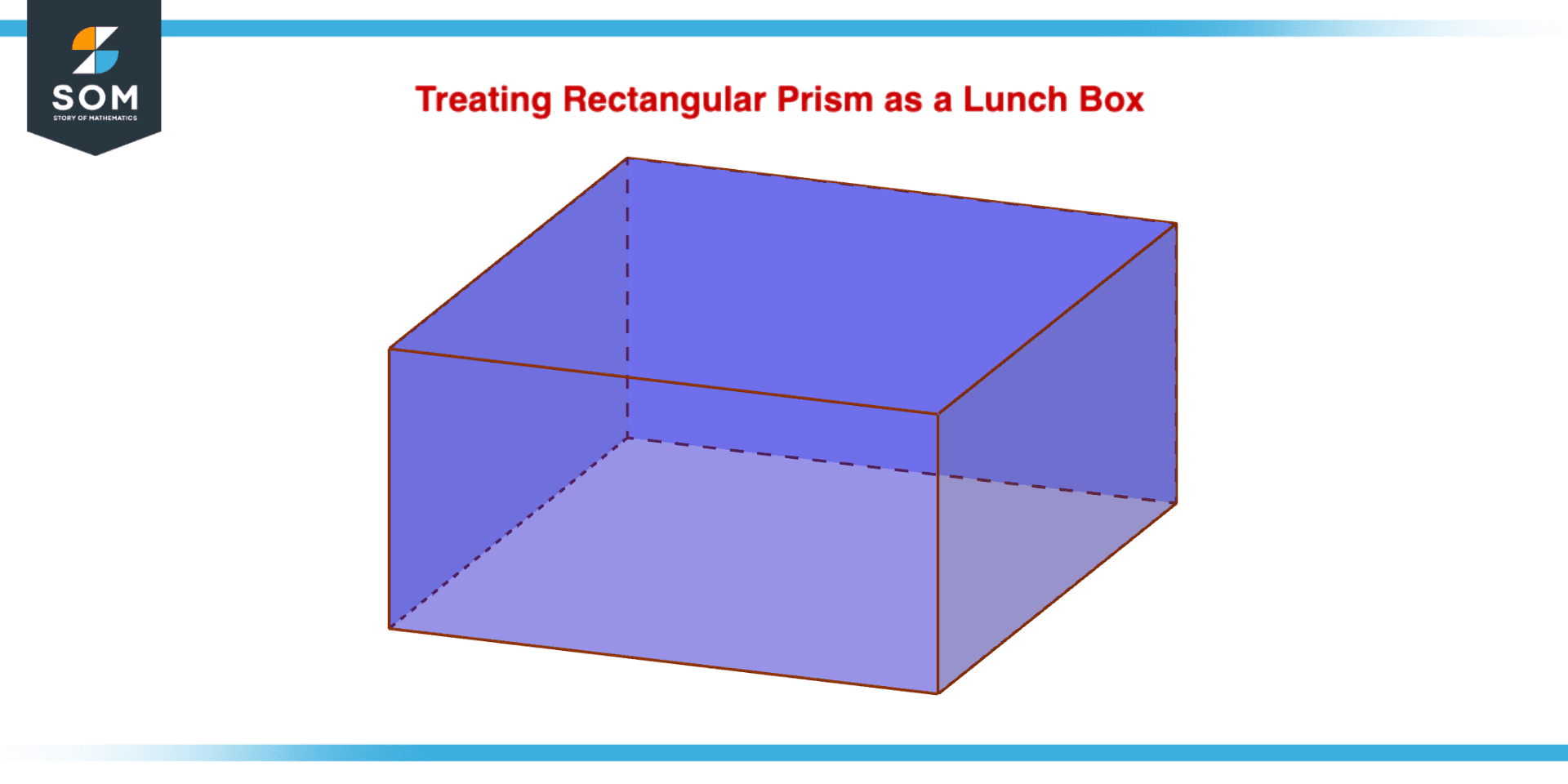
Figure 3 – Rectangular Prism as a Lunch Box

One example of a daily life scenario where a rectangular prism might be used is packing a lunch. Here’s how a rectangular prism could be used in this scenario.

1. Pick a lunchbox: A lunch box is often a rectangular prism with adjustable length, breadth, and height to hold various food items.
2. Make a lunch: To make the most of the available space in the lunch box, the foods being packed, such as sandwiches, fruits, and snacks, can be arranged. The amount of food that can fit within the lunch box may be calculated using its length, width, and height.
3. Close the Lunch Box: After the food has been packed, the lunch box can be closed and kept shut with a latch or zipper. The lunch box’s rectangular prism form helps to retain the food and protect it from leaking out.
4. Transport the Lunch Box: The lunch box’s handle or shoulder strap can be used to transport it to school or work. The lunch box is convenient to keep and travel thanks to its rectangular prism design.
5. When it’s time to eat, open the lunchbox so that the contents can be taken out and devoured. The lunch box’s rectangular prism design makes it simple to reach the contents within.

Solved Examples With Rectangular Prisms

Example 1

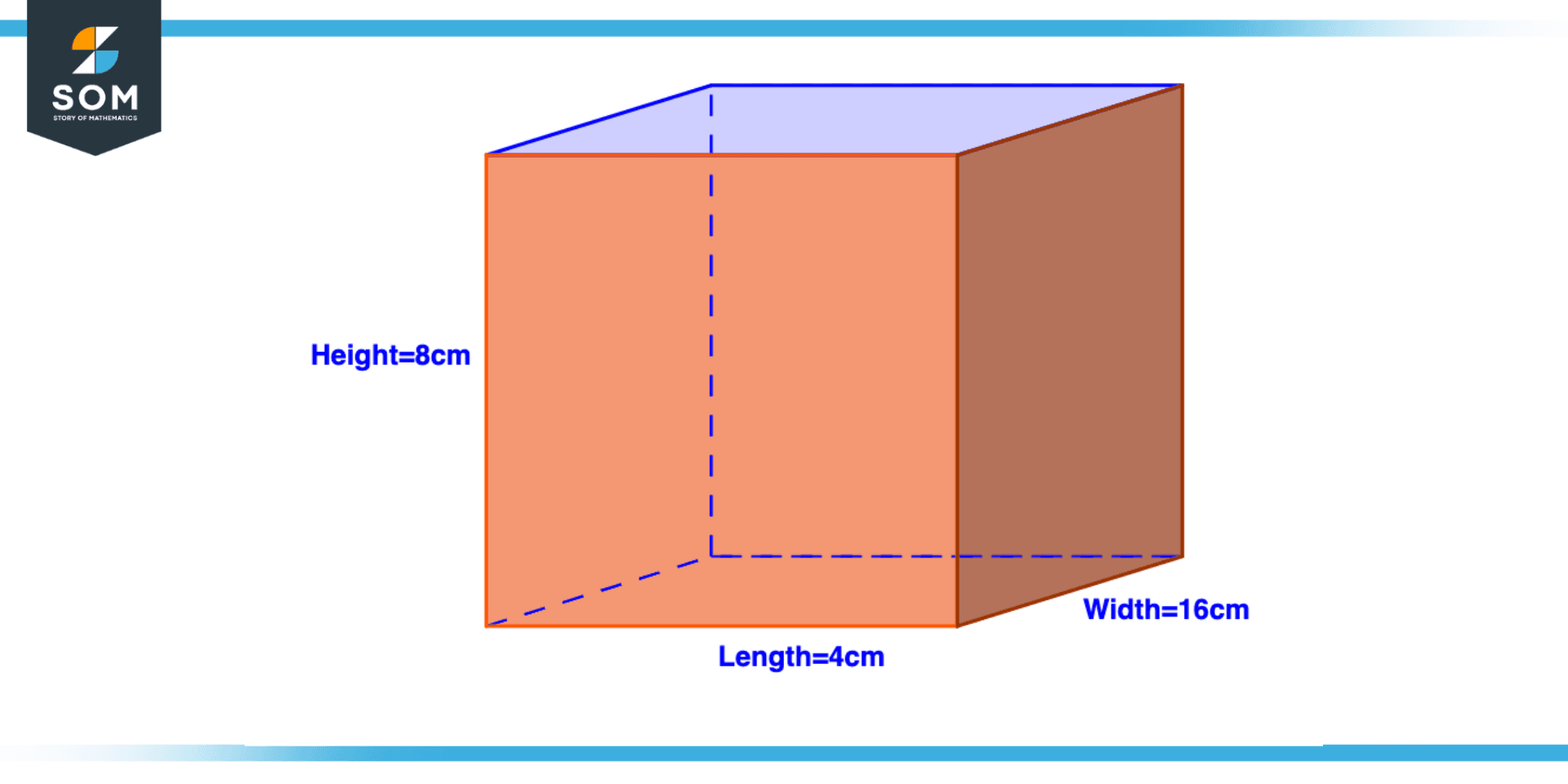
Figure 4 – Finding the volume of rectangular prism an example

Consider a rectangular prism having a length of 4 cm, a height of 8 cm, and a width of 16 cm. Calculate the volume of this rectangular prism.

Solution

Length = 4 cm

Height = 8 cm

Width = 16 cm

Volume = ?

As we know:

Volume = Length x Width x Height

Volume = 4 cm x 16 cm x 8 cm

Volume = 512 cm$^{3}$

Example 2

Consider a rectangular prism having a length of 4cm, a height of 8cm, and a width of 16cm calculate the surface area of this rectangular prism.

Solution

Length = 4 cm

Height = 8 cm

Width = 16 cm

Volume = ?

As we know:

Surface Area = 2LW + 2LH + 2WH

Surface Area = 2(4 cm)(16 cm) + 2(4 cm)(8 cm) + 2(16 cm)(8 cm)

Surface Area = 448 sq.cm

All mathematical drawings and images were created with GeoGebra.

Rectangle Definition < Glossary Index > Recurring Decimal Definition