Recurring Decimal|Definition & Meaning

What Is a Recurring Decimal? 

A decimal number that only contains the decimal point and consists of digits that repeat after a set interval following the decimal is said to have a recurring decimal, also known as a repeating decimal.

For instance, 91.1279…, 5265.975975… etc. The type of digits that come after the decimal point, as well as whether or not those digits repeat, don’t repeat, end, or don’t end, all play a role in determining the classification of decimals into one of several distinct groups (infinite digits after the decimal point).

This article will teach approximately recurring decimals, recurring decimals as rational numbers, and recurring decimals converted to fractions, along with examples of how these problems might be addressed.

Recurring decimals, often known as recurring decimals, have a predetermined list of terms to the right of the decimal that is repeated consistently. The division of decimal numbers into terminating and non-terminating decimals and repeating and non-repeating decimals is known as the classification of decimal numbers.

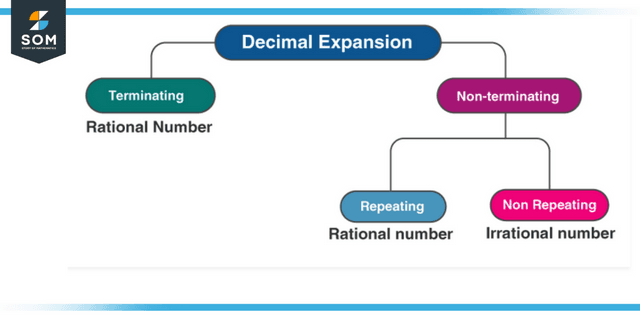
Figure 1: Representation of Decimal expansion

Recurring Representation of the Decimal System

A non-terminating decimal is said to be recurrent when a digit or a sequence of numbers repeats itself repeatedly and repeatedly, even without concluding. This type of decimal is known as a recurring decimal.

Most of the time, bars are placed on the repeating digits in recurring decimals. For instance, in the expression 0.5555…..=0.5¯, the repeating term in decimals is expressed by a bar on top of the recurring component.

When dealing with recurring decimals, dot notation is utilized. The dot placed over a certain number or group of digits indicates which number is repeating itself. For instance, 0.89 is equivalent to 0.8999… and 0.56 is equivalent to 0.56565656..

Recurring Decimals to Form Rational Numbers

Using the long division method, a rational number can be expressed as a decimal number with the same numerical value as the rational number itself. We need to use the long division method to divide the rational number, and the quotient we get is the rational number’s representation in decimal form. There are two distinct kinds of decimal expansions that can be used to represent a rational number:

• Terminating
• Non-terminating but repeating

For instance, the expression 5/6 = 0.833333… is an example of a decimal that does not terminate. At the end of the decimal, you’ll see that the digit 3 appears multiple times. Put a bar on top of the first number of the number three to show that it is repeated. Thus, 5/6 = 0.83 bar.

Conversion From Decimal to Fraction Recurring

One of the many ways a decimal number can be represented is a recurring decimal, which is one of the other sorts and forms. Numbers that are said to have recurring decimals are those in which the decimal digits repeat themselves. For your convenience, the procedures necessary to convert recurring decimals to fractions are listed below.

Step 1: We define x as the enlarged version of the recurring or repeating decimal.

Step 2: Count how many digits appear more than once. Let them have their n.

Step 3: Perform the multiplication of the recurring decimal by 10n.

Step 4: To get rid of the recurrent section, subtract the outcome of Step 1 from the outcome of Step 3.

Step 5: Determine the value of x and write the result as a fraction in its basic form.

For instance, if x = 0.23232323, then the number of recurring digits is two, which means that we need to multiply with 10 to the power 2 = 100. 100x = 23.23232323, and when we subtract these two equations, we obtain 99x = 23, which tells us that x = 23/99.

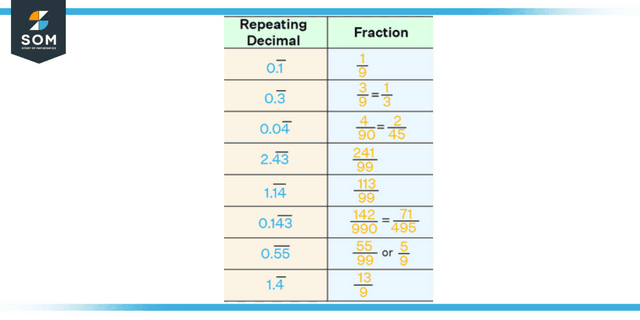
Figure 2: Representation of recurring decimal to fraction

Difference Between Recurring and Terminating Decimals

The remainder of terminating decimals is always 0, whereas the remainder of repeating decimals tends to repeat after a certain point. Recurring decimals correlate to repeating decimals because the remainder continues to repeat after that point.

Difference Between Recurring and Non-recurring Decimals

Decimal numbers that do not recur their values after the decimal point are not considered recurring decimal numbers. On the other hand, decimal numbers repeating their values after the decimal point are referred to as recurring decimal numbers.

Figure 3: Difference between recurring and non-recurring decimals

Properties Regarding Recurring Decimals

A few properties of recurring decimals are discussed below:

• These decimal numbers are simply periodic. It indicates that following the decimal point, the digits will repeat themselves at regular intervals.
• We can write recurring decimals by placing a bar sign or dots above the digits that repeat after the decimal point. This will make the decimals seem as recurring.
• We can express recurring decimals as rational numbers through the use of fractions.

How Can You Demonstrate That a Decimal Is Repeating Itself?

If a digit or set of digits continues to repeat indefinitely beyond the decimal point, we refer to that decimal number as having recurring digits. A bar or a pair of dots placed over the initial and final digits of the consistent pattern might be used to illustrate the pattern portion that is intended to be repeated.

Examples of Recurring Decimals

Example 1

Identify the following terms as recurring or non-recurring values:

0.767676, 10/3, 9.8743

Solution

0.767676 is a recurring number.

10/3 = 3.33333 is a recurring number.

9.8743 is a non-recurring number.

Example 2

Convert the following repeating decimal value into a fraction:

6.234234

Solution

Count the repeating digits and multiply the decimal by 10 that many times:

6.234234 * 1000

6234.234234

Now subtract the original decimal from the above value:

6234.234234 – 6.234234 = 6228

Write the equation and solve for the fraction:

1000x – x = 6228

999x = 6228

x = 6228/999

x = 692/111

All images/graphs are created by using GeoGebra.

Rectangular Prism Definition < Glossary Index > Reduce Definition