Reduce|Definition & Meaning

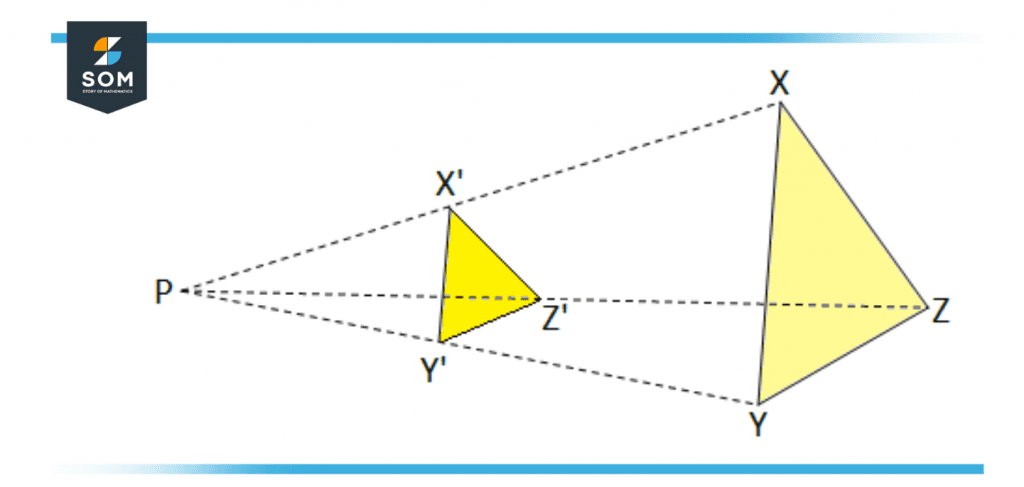
Figure 1 – Reduce Transformation

What Does Reduce Do in Math? 

In mathematics, the term “reduce” can have different meanings depending on the context. In general, it refers to the process of simplifying or bringing an expression or equation to a simpler or more standard form.

For example, in algebra, reducing an expression means to simplify it by combining like terms, such as combining 3x and 4x into 7x.

Another example is reducing a fraction, which means to divide both the numerator and denominator by their greatest common factor (GCF) to make the fraction in its simplest form.

In trigonometry and calculus, reducing a function means to simplify it by applying algebraic and trigonometric identities, or by applying the properties of derivatives and integrals.

In linear algebra, reducing a matrix means to transform it into a simpler form by applying elementary row operations such as swapping rows, multiplying rows, and adding rows.

In number theory, reducing a number means to divide it by a common divisor to obtain the greatest common divisor (GCD) of two or more numbers.

In general, reducing a mathematical expression means to simplify it by applying the appropriate mathematical rules and procedures to make it easier to understand, solve, or manipulate.

Advantages and Disadvantages of Reducing in Math

Advantages of reducing a mathematical expression or equation:

• Simplifies the expression or equation, making it easier to understand, solve, or manipulate.
• Allows for the identification of patterns or relationships within the expression or equation.
• Allows for the identification of equivalent expressions or equations, which can be useful in solving problems.
• Can make it easier to check the correctness of a solution.

Disadvantages of reducing a mathematical expression or equation:

• Can be time-consuming, especially for more complex expressions or equations.
• Can be error-prone, if the steps are not done correctly, it might lead to wrong results.
• Can make the expression or equation more difficult to understand for someone who is not familiar with the reduction method used.
• Can make it more difficult to check the correctness of the solution if the expression or equation is highly reduced.

In general, reducing mathematical expressions and equations is a powerful tool for solving problems and understanding mathematical concepts. However, it is important to consider the context and the intended audience when reducing an expression or equation, as it can sometimes be more beneficial to leave it in a less-reduced form.

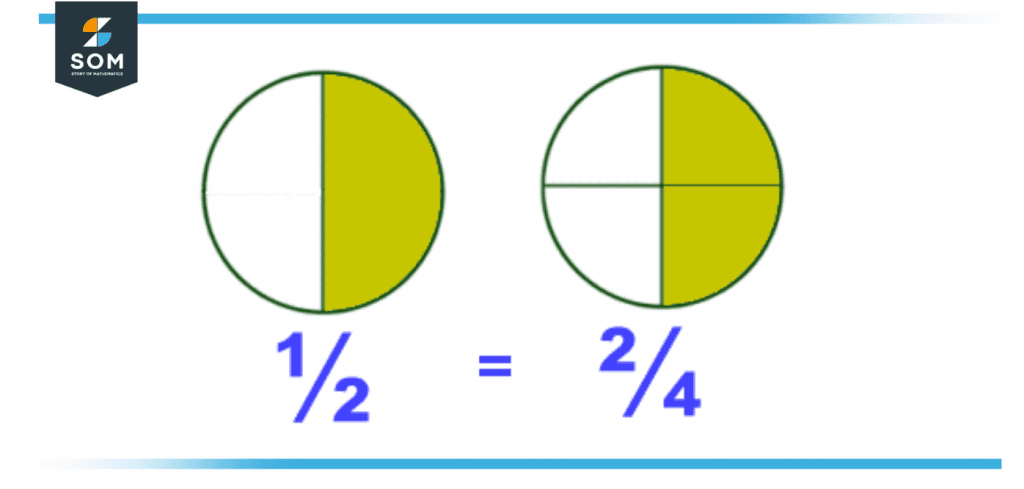
Figure 2 – Reduce Fractions

How Do I Reduce a Fraction?

To reduce a fraction means to divide both the numerator and denominator by their greatest common factor (GCF) to make the fraction in its simplest form. Here is the process of reducing a fraction:

Find the GCF of the numerator and denominator: The GCF is the largest number that divides both the numerator and denominator without leaving a remainder. You can find the GCF using the Euclidean algorithm or by listing the prime factors of both the numerator and denominator and seeing which ones are common.

Divide both the numerator and denominator by the GCF: Once you have found the GCF, divide both the numerator and denominator by it. This will give you the reduced form of the fraction.

Example: Reduce the fraction 15/45.

First, we find the GCF of 15 and 45.

Factors of 15: 1, 3, 5, 15

Factors of 45: 1, 3, 15, 45

Divide both the numerator and denominator by the GCF, so 15/15 = 1 (numerator) and 45/15 = 3 (denominator). The reduced form of the fraction is 1/3.

It’s important to note that if the GCF is 1, then the fraction is already in its simplest form, and no further reduction is needed.

It’s also possible to use a calculator to reduce a fraction. Most of them have a specific button or function to reduce a fraction.

In general, reducing a fraction is important in order to make the fraction easier to understand and work with, and it’s a fundamental step in solving many mathematical problems.

What Happens in a Reduction?

In a reduce operation, a function is repeatedly applied to the elements of a sequence or iterable, such as a list or an array, in order to combine or “reduce” them into a single value. The function that is applied is often called the “reduce function” or “accumulator function,” and it should take two arguments and return a single value. 

The reduce operation starts with the first two elements of the sequence, applies the reduce function to them, and then uses the result of that as the first argument for the next application of the reduce function, and so on until a single value is obtained.

Is Reduce Positive or Negative?

In general, “reduce” can have both positive and negative connotations depending on the context in which it is used.

Positive connotations of “reduce” might include things like reducing waste or reducing pollution, which is generally considered good for the environment or society as a whole.

Negative connotations of “reduce” might include things like reducing staff or reducing benefits, which can have negative impacts on individuals or groups.

In summary, “reduce” is a neutral term, but its connotation depends on the context of the usage.

Figure 3 – Reduce Method of Drawing

What Is the Reduced Method of Drawing?

The reduced method of drawing, also known as “reductive drawing,” is a technique in which an artist begins with a detailed, fully rendered image and then gradually removes or simplifies elements to create a more minimal and abstract final product. 

This method is often used in charcoal drawing, but it can also be applied to other mediums such as pencil, ink, or even digital drawing.

The process starts by drawing a detailed image, then the artist will erase or cover parts of the image, gradually simplifying and removing details. The goal is to reveal the essential forms and shapes of the subject and to simplify the image to its most basic, yet still recognizable, form.

Reductive drawing is a great way to explore the underlying structure of a subject and to experiment with different ways of simplifying and abstracting an image. It can also help artists to develop their ability to see and understand the basic shapes and forms that make up an image, which is an important skill for any artist to have.

Some Examples of Reduce

Example 1

Reduce the following expressions:

1. 2x + 3x – 5x.
2. 8/12
3. (x + y)²
4. 2x + 3 = 7

Solution

Answer to part (a): 0x

Answer to part (b):2/3

Answer to part (c): x² + 2xy + y^2

Answer to part (d): x = 2

Example 2

Try to reduce the following expression:

1. sin²(x) + cos²(x)
2. x² + 5x + 6
3. log(a³ * b²)
4. 3(2x + 4) – 5(x – 2)

Solution

Answer to part (a): 1

Answer to part (b): (x + 3)(x + 2)

Answer to part (c): log(a³) + log(b²)

Answer to part (d): 6x + 6 – 5x + 10 = x + 16

All images were created with GeoGebra.

Recurring Decimal Definition < Glossary Index > Reflection Symmetry Definition