JUMP TO TOPIC
Reflection Symmetry|Definition & Meaning
Definition
A geometrical figure which is identical to its reflection is said to possess reflection symmetry. For example, a square and a rectangle both have reflection symmetry since their mirror image is exactly identical to the original figures. Shapes that have reflection symmetry have a line of symmetry that divides the figure into 2 identical parts.
Mirror Symmetry (also known as Line Symmetric or Mirror Symmetric) is evident since one half reflects the other.
A Symmetrical item can be split into two halves so that one half becomes the mirror reflection of the other half. If none of the parts is a mirror image of the other, the thing is described as asymmetric. Symmetric things may be found everywhere, in nature, architecture, art, etc.
Figure 1 below shows the reflection symmetry of the triangle.
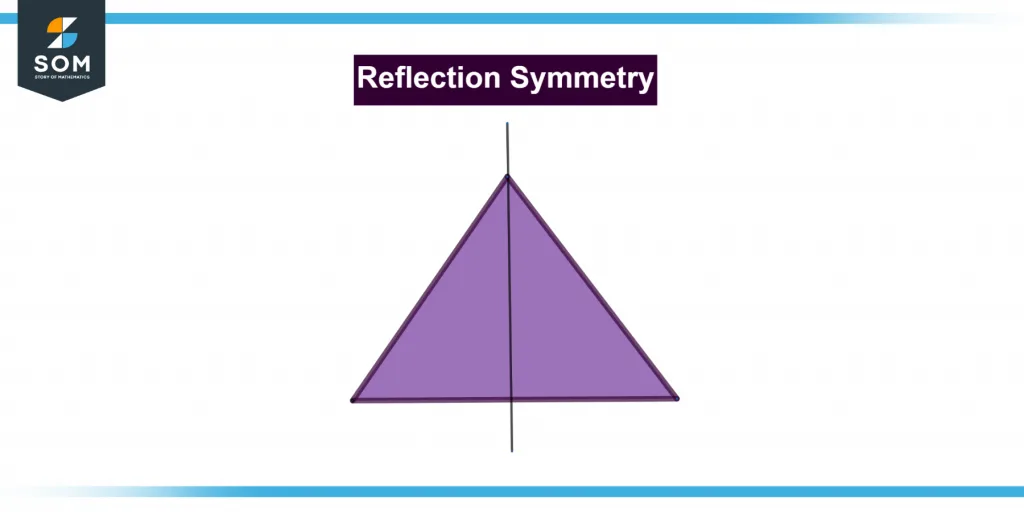
Figure 1 – Representation of reflection symmetry.
What Exactly Is Reflection Symmetry?
Reflection symmetric is a symmetry that revolves around reflections. It is characterized as reflection symmetry if, at most, one line splits an image into two halves, with one half being the mirror reflection of the other.
Line symmetry is another name for it. The line of symmetry might be horizontal, vertical, slanted, or any other orientation.
A line of symmetry is the line along which a mirror may be held so that one half appears as that of the reflection of its counterpart.
One or more streams of reflection symmetry can exist in a figure. The symmetry line can go in any direction.
Recognizing Symmetry in Reflection
The first thing you’ll notice is that one side mirrors the other. Consider folding a rectangular form along either symmetry line, with each half properly aligned; this is symmetry. A shape with reflection symmetry must have at least one line of symmetry.
One of the most important aspects of symmetric reflection is that one of two symmetrical sides follows a lateral invert, which means that when viewed in a mirror, the left side appears to be the right side.
Symmetry Line
The Mirror Line (also known as the Line of Symmetry) can run in any direction.
However, four popular directions are called after the line they form on the conventional XY graph.
Figure 2 below shows the symmetry line.
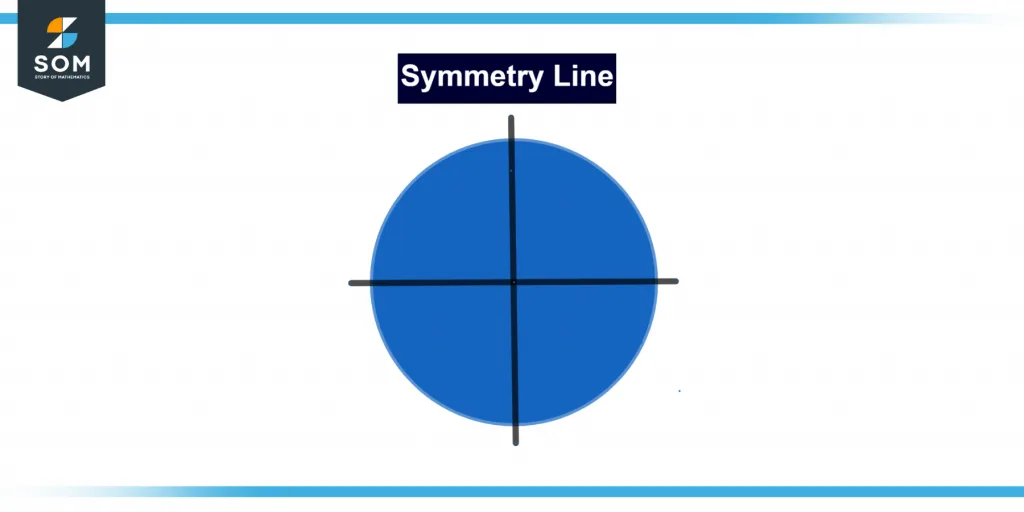
Figure 2 – Representation of a symmetry line.
Samples of Reflection Symmetry
The following are some common instances of reflection symmetry:
- A square has four symmetric lines, which are the lines that connect the center point of opposing sides and the lines that connect the vertices.
- A rectangular form is defined by two symmetry lines connecting the center point of opposing sides.
- A general trapezoid will lack reflection symmetry, but rather a rotationally symmetric trapezoid would because the line connecting the centers of the bases is a symmetry line.
- Reflection symmetry may be seen in the reflection of trees in clear blue water and the mirror on hills in a lake.
Symmetry Axis
The symmetry axis is a hypothetical straight line that splits a form into two identical sections, resulting in one component being the mirror reflection of the other.
When the two sections are folded along the axis of symmetry, they superimpose. The straight line is also known as the line of symmetry/mirror line. This line might be horizontal, vertical, or diagonal.
The symmetry axis is a direct line that makes an object’s form symmetrical. The symmetry axis produces identical reflections on all four sides. It might be vertical, horizontal, or lateral in orientation. The two sides of an object are similar if we fold or unfold it according to the axis of symmetry.
Distinct forms have different symmetry lines. A square has four symmetric lines, a rectangle has two, a circle has unlimited lines of symmetry, and even a parallelogram has one. A regular polygon with ‘n’ edges has ‘n’ symmetry axes.
Is There Symmetry in a Parallelogram?
A parallelogram may appear symmetrical at first glance. However, it isn’t symmetric along one of the reflection axes.
Inkblot paper also exhibits reflection symmetry. Pour a little ink and water over one of the paper’s sides. Fold the document in half and press with your palm. Spread the paper to view the symmetric design along the fold line. The plane of reflection is the fold line.
Figure 3 below shows symmetry in a parallelogram.
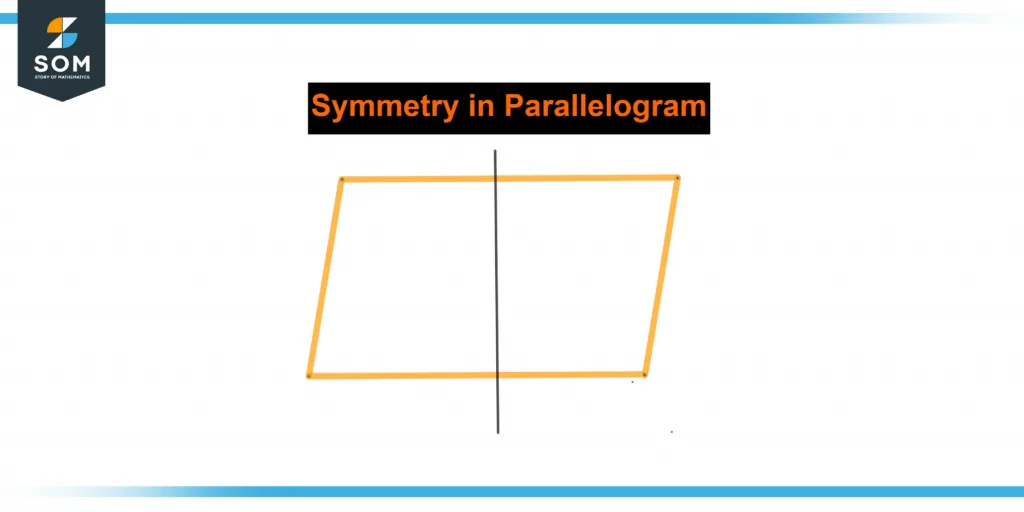
Figure 3 – Symmetry Lines in a Parallelogram.
Symmetry Lines in a Parallelogram
The parallelogram is, in fact, a quadrilateral with parallel & equal sides. The imaginary line generated by scrunching a figure to acquire the symmetrical halves is known as a line of symmetries.
Thus, the parallelogram’s lines of symmetry are the lines that split each parallelogram in and out of identical halves. Likewise, the symmetric lines together in a parallelogram vary depending on their kind.
A parallelogram’s lines of symmetry are the lines that divide it into two halves, each of which is the carbon copy of the other. Parallelograms are classified based on their forms, line segments, and corners. As a result, they have various symmetry lines and a varied number of symmetry lines.
By folding a form and looking again for a Line of Symmetry, we may determine if it is symmetrical. If the folded half fits precisely on a top, with all corners and edges matching, the folded line is a Line of Symmetry, and the form is symmetrical along its length, width, or diagonals.
Example of Reflection Symmetry
Which of the following lines splits the parabolic 3x2 – 12 x + 5 = 0 into two equal parts?
Solution
When we compare the standardized format of the quadratic formula given as ax2 + bx + c, we get the values of a, b, and c from this formula
a is equal to 3, b is equal to -12, and c is equal to 5.
We know that the x = -b / (2a) is the axis of the symmetry equation.
Putting the values in the equation, we get
x = -(-12) / (2 * 3) = 12 / 6 = 2
So, x = 2 is the answer.
All images are made using GeoGebra.
