JUMP TO TOPIC
Regular|Definition & Meaning
Definition
In mathematics, regular means different things depending on which branch of mathematics we look at. Generally, it refers to something that is well-defined, often predictable, and easily identifiable because of unique patterns and characteristics. For example, a regular shape (in geometry) is defined as one where all the sides and angles are equal in length (as in a square).
Figure 1 shows a square which is a regular polygon.
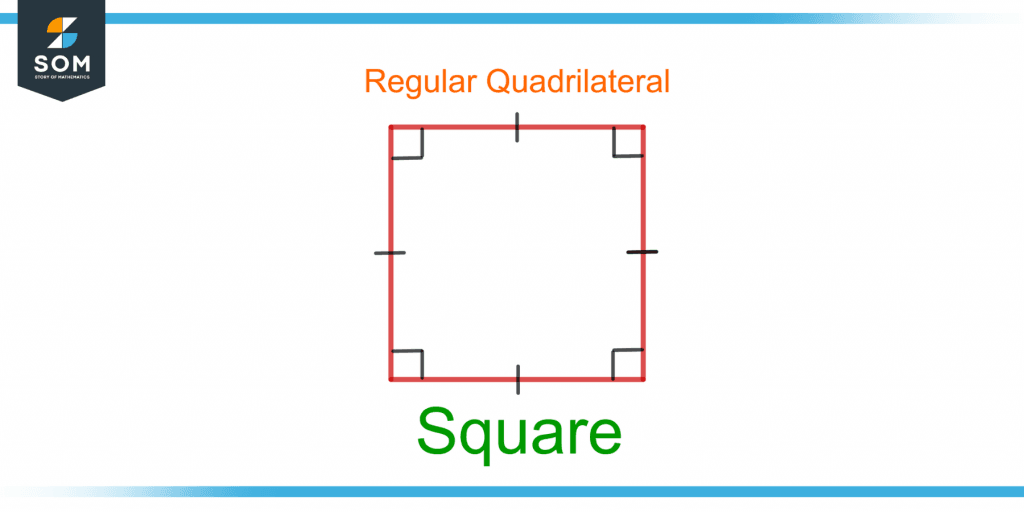
Figure 1 – Square – An Example of a Regular Polygon (A Quadrilateral)
Polygons
A polygon is a closed two-dimensional figure with no curved surfaces and is a plane or flat shape having different numbers of edges and vertices. Figure 2 shows three different shapes of which only one is a polygon.
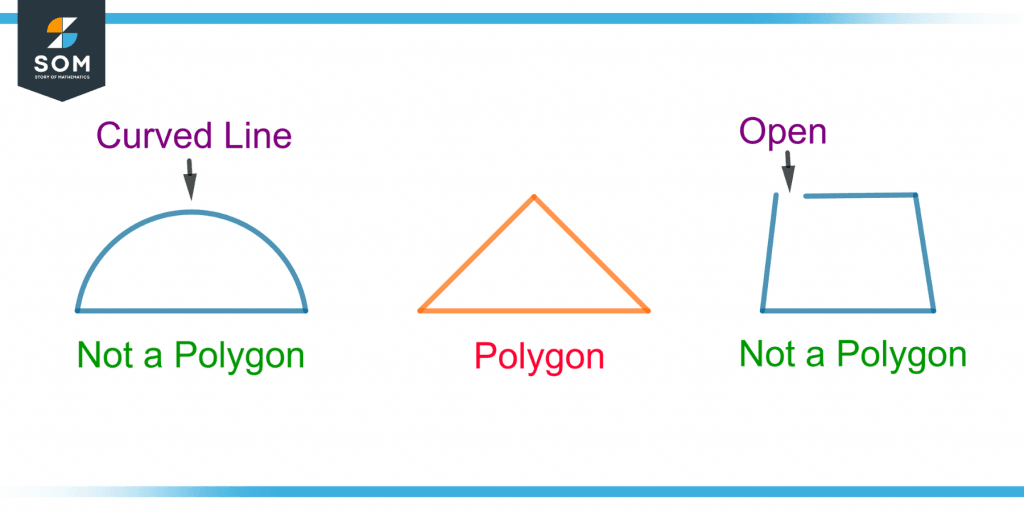
Figure 2 – Demonstration of a Polygon and Two Non-polygon Shapes
A corner or the point where two edges meet is known as the vertex of a polygon. A polygon consists of more than two vertices.
The two essential features of a polygon that define its regularity are its sides and angles.
Sides
The edges of a polygon are also known as its sides. The sides are the line segments that make the polygon. Different polygons have different numbers of sides.
Angles
The angles of the polygon are the internal angles formed between two adjacent sides inside the polygon. A polygon has a number of angles equal to the number of vertices.
Figure 3 shows the sides and the internal angles of a triangle.
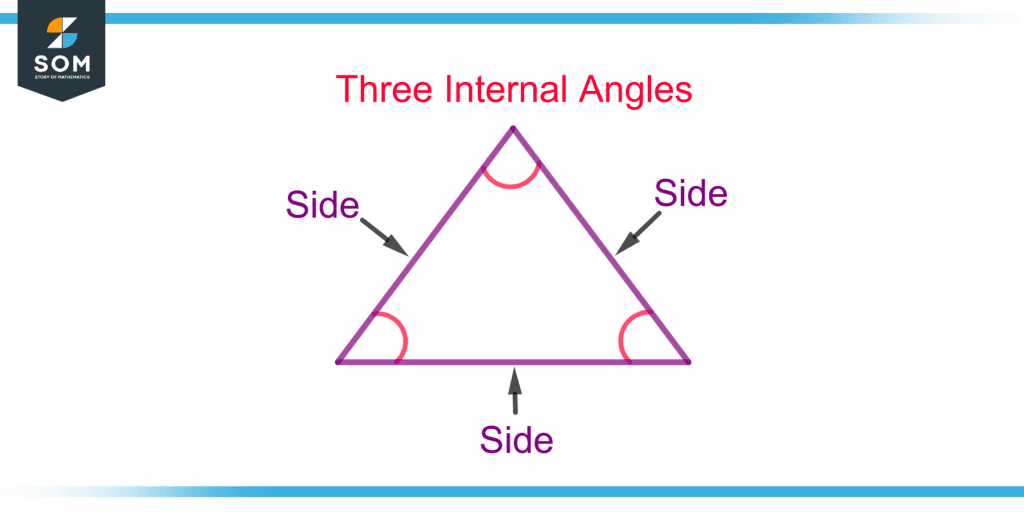
Figure 3 – Demonstration of Sides and Internal Angles of a Triangle (Polygon)
For a regular polygon, all the sides and internal angles must be equal to each other.
Different Types of Regular Polygons
There are different types of regular polygons depending on the number of sides.
Equilateral Triangle
A triangle consists of three sides and three internal angles. An equilateral triangle has all the sides of equal length and each angle equal to 60°, making a sum of 180° of all the internal angles.
Regular Quadrilaterals
A quadrilateral consists of four sides and four angles. Different types of quadrilaterals depend on the length of the sides and the measure of their angles. A square, rectangle, and parallelograms are quadrilaterals with the sum of 360° of all the internal angles.
A square is a regular quadrilateral with each internal angle equal to 90°.
Regular Pentagon
A pentagon consists of five sides, five vertices, and five internal angles. A regular pentagon has each internal angle equal to 108°, with the sum of all angles equal to 540°.
Regular Hexagon
A regular hexagon has six internal angles, each measuring 120°, and six sides of equal length.
Regular Heptagon
A heptagon has seven equal sides and internal angles. A regular heptagon has an internal angle equal to 128.57° and all sides of equal length. All the internal angles of regular heptagon add to 900°.
Regular Nonagon
A nonagon consists of nine sides and nine angles that sum to 1260°. A regular nonagon has nine equal sides and angles, with each internal angle equal to 140°.
Regular Decagon
“Deca” means ten, so a decagon has ten edges and ten vertices. A regular decagon has all the sides of equal length, with each interior angle equal to 144°. The sum of the internal angles of a decagon equals 1440°.
Figure 4 shows all types of regular polygons.
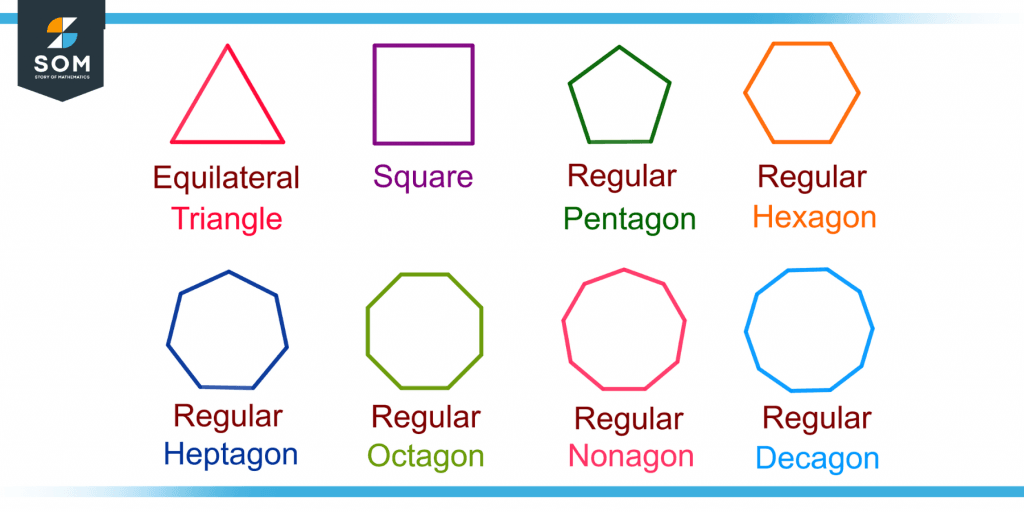
Figure 4 – Different Types of Regular Polygons
Lines of Symmetry of Regular Polygons
The lines of symmetry in a regular polygon are imaginary lines that divide a regular polygon into equal parts and pass through its center. The lines of symmetry of a regular polygon equal its number of sides.
Figure 5 shows the lines of symmetry of an equilateral triangle.
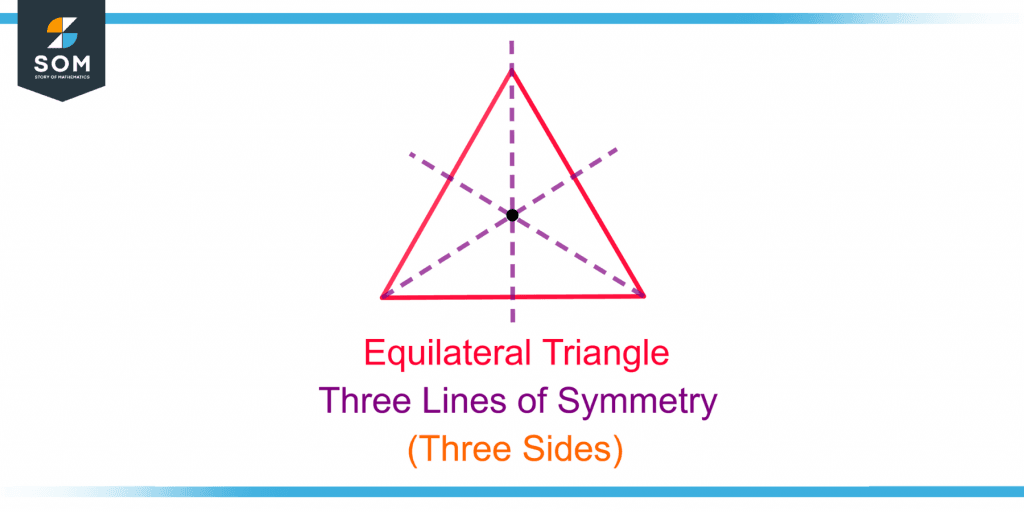
Figure 5 – Demonstration of Lines of Symmetry of an Equilateral Triangle
Rotational Symmetry of Regular Polygons
The rotational symmetry of a regular polygon is a similar view of the polygon compared with the original view when rotated at some degrees other than 360°. The order of a regular polygon’s rotational symmetry equals the number of its sides.
The angle at which the polygon is rotated is known as the angle of rotation. It can be calculated by dividing 360° by the total number of sides of the polygon. For example, a pentagon is rotated at 360°/5 = 75° to check its rotational symmetry.
Irregular Polygons
The polygons having either unequal lengths of sides or unequal interior angles or both are known as irregular polygons. The following are some of the irregular polygons.
Irregular Triangles
There are three main types of irregular triangles.
Isosceles Triangle
A triangle with two equal sides out of three sides is known as an isosceles triangle. The two interior angles opposite the two sides of equal length are also equal. All the sides and angles are not equal, which makes it an irregular polygon.
Scalene Triangle
A scalene triangle has all the sides of unequal length and its three interior angles of unequal measure; hence it is an irregular polygon.
Right-angle Triangle
A right-angle triangle has a 90° angle which makes one angle unequal to the other two angles. Also, the hypotenuse(the side opposite to the right angle) is the longest side, making one side unequal to the other two sides.
A right-angle triangle can have all three angles and sides unequal in measure; therefore is considered an irregular polygon.
Figure 6 shows all the irregular triangles.
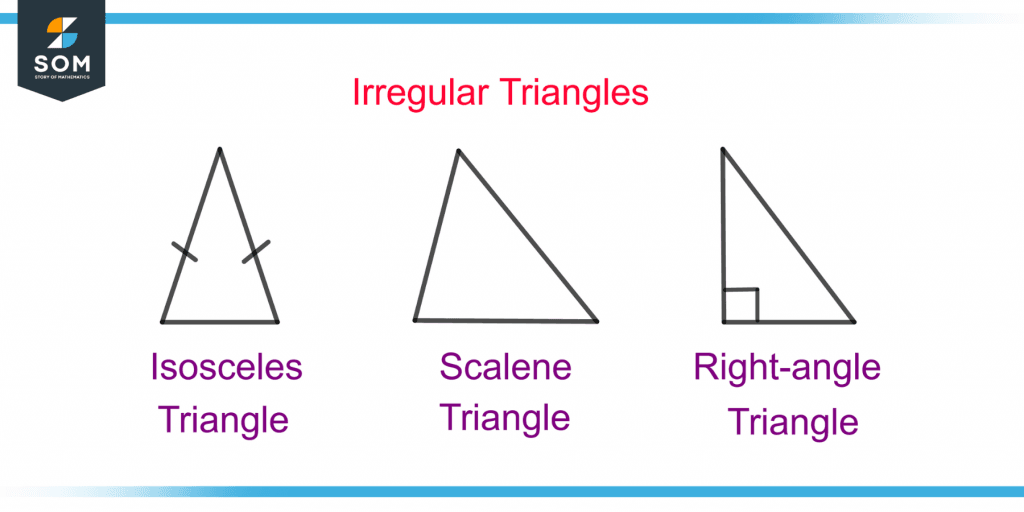
Figure 6 – Different Types of Irregular Triangles
Irregular Quadrilaterals
The irregular quadrilaterals include rectangles, trapezoids, rhombus, parallelograms, and kites.
Rectangle and Parallelogram
A rectangle and parallelogram have two opposite sides of equal length, but not all sides are equal, making them irregular polygons.
Rhombus
A rhombus has all equal sides but has only the opposite angles equal, not all the angles making it an irregular polygon.
Trapezoid
A trapezoid is an irregular polygon with two parallel sides having all the sides of unequal length.
Kite
A kite has two adjacent sides in pairs of equal length which makes it irregular. Figure 7 shows all the irregular quadrilaterals.
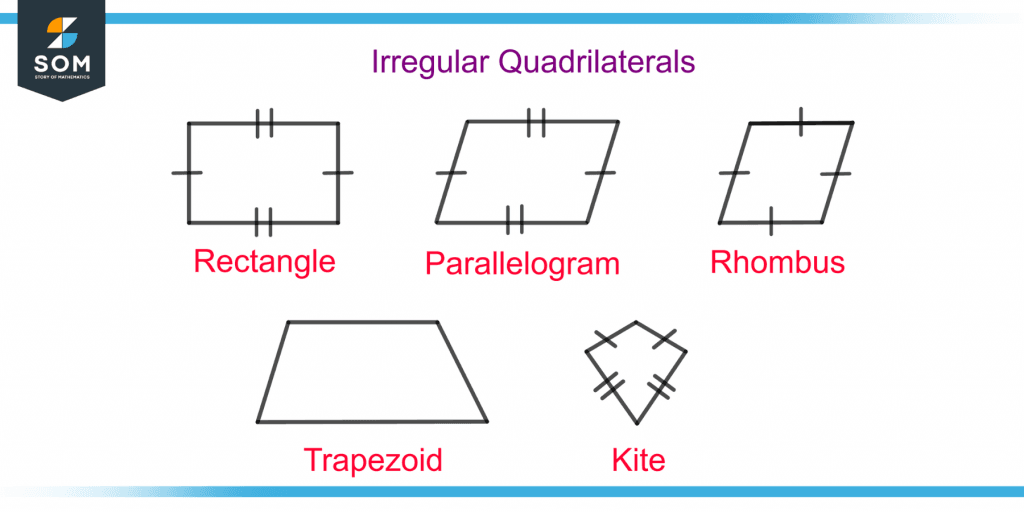
Figure 7 – Different Types of Irregular Quadrilaterals
A Regular Polyhedron
A regular polyhedron has all its faces as regular polygons congruent to each other, and an equal number of faces joined alike at each vertex. For example, a cube is a regular polyhedron having congruent squares as its faces.
Example
Figure 8 shows two hexagons, A and B.
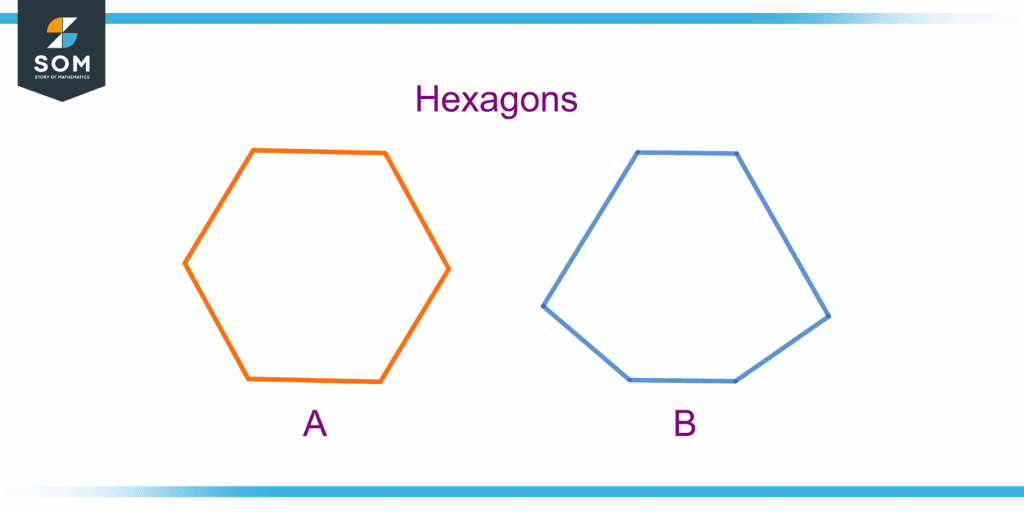
Figure 8 – Identifying a Regular Hexagon
Which is a regular hexagon? What is the order of rotational symmetry, and at what angle is it rotated to gain rotational symmetry? How many lines of symmetry are there in a regular hexagon? What is the sum of all the interior angles of a hexagon?
Solution
Hexagon A is a regular hexagon as it has all the sides of equal length compared to hexagon B.
A regular hexagon’s rotational order of symmetry is six, which is equal to the number of its sides. The angle at which the hexagon is rotated to gain symmetry is 360°/6 = 60°.
A regular hexagon has six lines of symmetry passing through its center.
As an interior angle of a regular hexagon equals 120°, the sum of the interior angles is calculated by adding 120° six times or multiplying 120° by six, which gives:
Sum of Interior Angles of a Hexagon = 120° ✕ 6 = 720°
All the images are created using GeoGebra.
