JUMP TO TOPIC
Regular Polyhedron|Definition & Meaning
Definition
A regular polyhedron is a three-dimensional, closed shape where all the faces are identical regular polygons. The length of all sides and all angles are, therefore, equal. There are only nine regular polyhedra, five of which are convex and four are star polyhedra.
The faces of a platonic solid, also known as a regular polyhedron, are regular polygons that are congruent to one another. Another name for this type of solid is a regular polyhedron. Each of the polyhedral angles in such a regular polyhedron will always be the same. There are only five polyhedrons that are regular in shape.
Polyhedron’s Parts
Faces, vertices, and edges are the three different types of dimensions that make up a polyhedron. Each and every polyhedron is comprised of three essential elements: the faces, edges, and vertices.
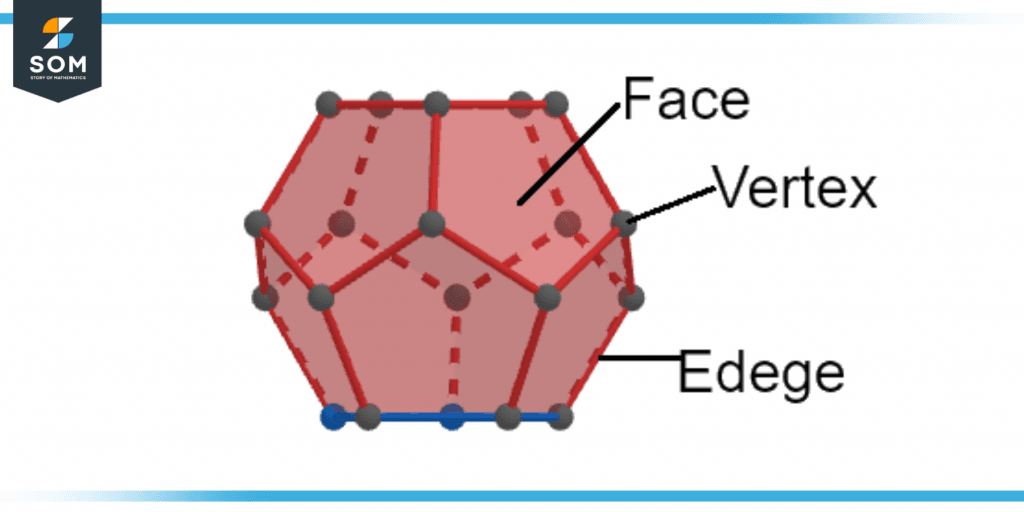
Figure 1 – Face, Vertex, and Edge of Regular Polygon
Take a look at the accompanying diagram, which illustrates a shape’s face, edge and vertex, and edges.
Face
The term “face” refers to the level surface that can be found on a polyhedron. The level surfaces that join to create a polyhedron are referred to as the object’s faces. These are two-dimensional polygons that make up these faces.
Edge
The line where the two faces come together is known as the edge. The line segments that are created when two areas or two flat faces come together to form a boundary are referred to as the edges.
Vertex
Vertices are defined as the points at which two edges meet with one another. Vertices are the points at which two edges of a polyhedron meet to form what is known as the vertex of a polyhedron. A polyhedron may contain more than one vertex at any given point. One may alternatively refer to these as the corners of the polyhedron.
A Deeper Dive Into Regular Polyhedra
A regular polyhedron is one with faces made out of regular polygons with a similar number of faces meeting at each vertex. This means that a regular polyhedron’s faces are congruent regular polygons, and its vertices are produced by the same number of faces.
The cube seems to be a regular polyhedron. However, a cuboid is not since its faces really aren’t congruent rectangles.
A polyhedron is a type of solid that has three dimensions and is constructed of polygons. It consists of faces that are flat, edges that are straight, and vertices.
The cube, the prism, and the pyramid are all examples of polyhedrons. Cones, cylinders, and spheres are not considered to be polyhedrons due to the fact that their surfaces are curved and their sides are not polygons.
The term “polyhedra” can also be used to refer to the plural form of “polyhedron.” Prisms, platonic solids, and pyramids are the categories that best describe them.
For instance, the platonic solid cube, the triangular prism, the square prism, the rectangle pyramid, and the square pyramid are all examples of polyhedrons. Take a look at the accompanying diagram, which demonstrates the various types of regular polyhedrons.
Formula of Polyhedron
Polyhedron Types There is a correlation between a polyhedron’s amount of edges, faces, and vertices. This relationship can be represented by a mathematical formula known as Euler’s Formula.
F + V – E = 2
where F = the count of faces, V = the amount of vertex, and E = the number of edges.
Using Euler’s Formula, we can quickly locate the missing polyhedron face. We can also determine whether or not a polyhedron with a specified number of faces exists. A cube, for instance, has six faces, eight vertices (corner points), and twelve edges. Using Euler’s formula, we shall determine if a cube is a polyhedron. F = 6, E = 12, V = 8,
Euler’s Calculation ⇒ F + V – E = 2 where F is the number of faces, V is the number of vertices, and E is the number of edges.
Changing the variables in the formula:
6 + 8 – 12 = 2 ⇒ 2 = 2.
Consequently, the cube is a polyhedron.
Types of Regular Polyhedron
The Platonic Solids are a collection of five different types of convex regular polyhedra.
In addition to that, there are four regular “star polyhedra” which are also referred to as Kepler-Poinsot solids.
Tetrahedron
Each of the tetrahedron’s faces is in the shape of an equilateral triangle, and the tetrahedron itself has four faces, six edges, and four vertices (corners).
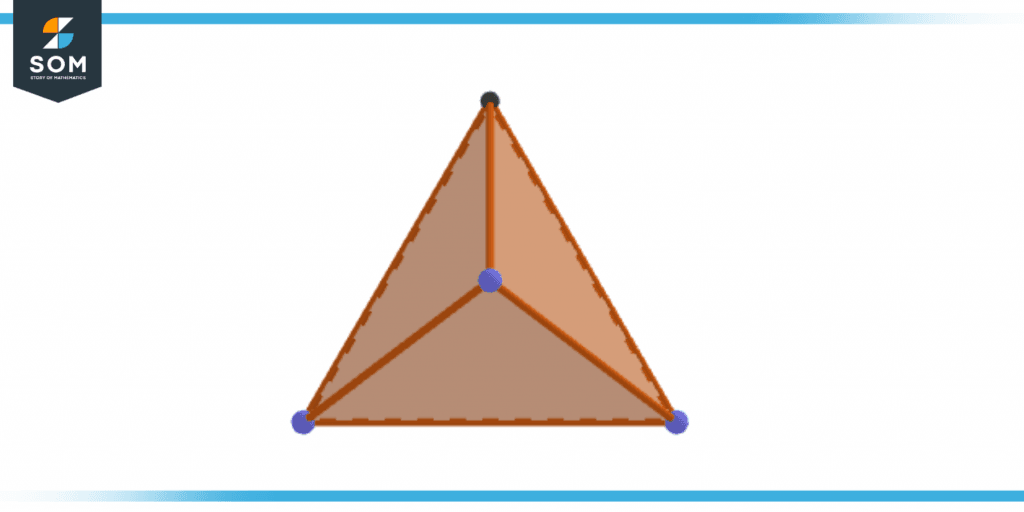
Figure 2 – Tetrahedron
- 4 triangular faces
- 4 vertices
- 6 edges
Cube
Each of the cube’s six faces is in the shape of a square, and the cube has twelve edges and eight vertices in total.
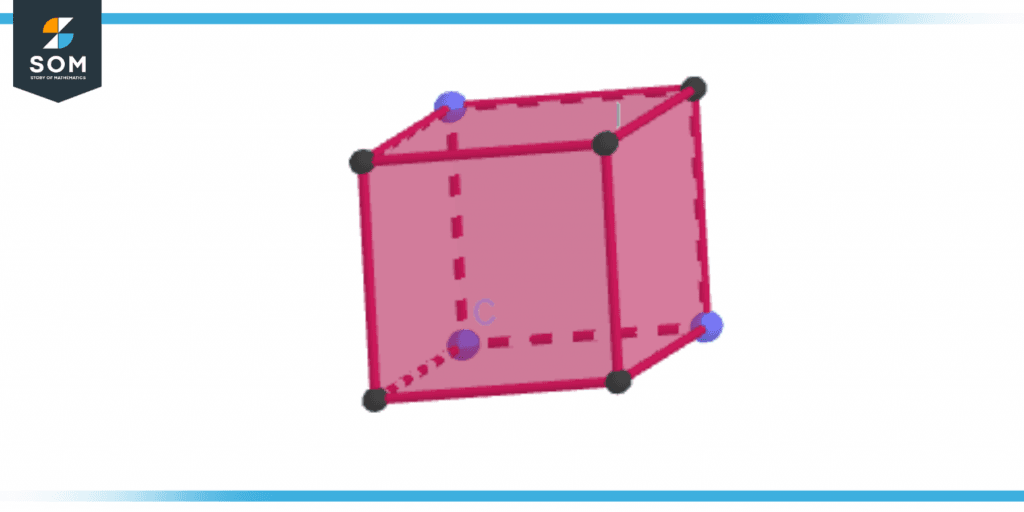
Figure 3 – Cube
- 6 square faces
- 8 vertices
- 12 edges
Regular Octahedron
An octahedron that is regular has eight faces, twelve edges, and six vertices, and each of its faces is in the shape of an equilateral triangle.
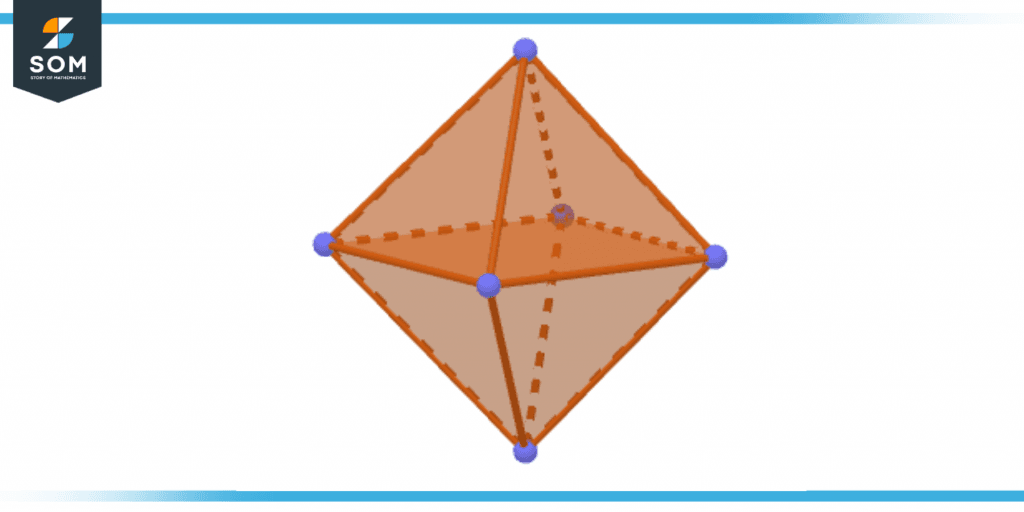
Figure 4 – Regular Octahedron
- 8 triangular faces
- 6 vertices
- 12 edges
Regular Dodecahedron
The shape of each face of a regular dodecahedron is that of a pentagon, and there are a total of twelve faces, thirty edges, and twenty vertices in a regular dodecahedron.
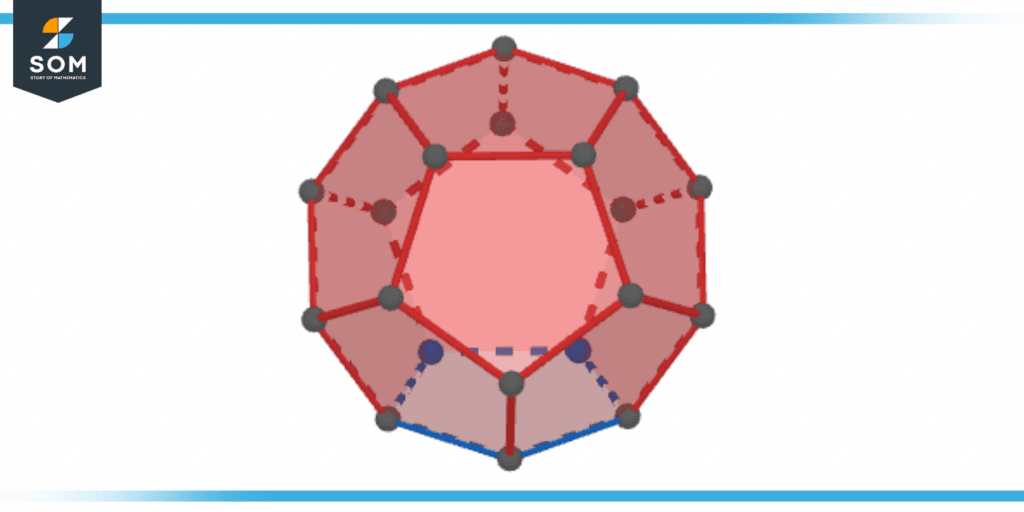
Figure 5 – Regular Dodecahedron
- 12 pentagonal faces
- 20 vertices
- 30 edges
Regular Icosahedron
Each face of a regular icosahedron is in the shape of an equilateral triangle, and the icosahedron has a total of thirty edges, twenty faces, and twelve vertices.
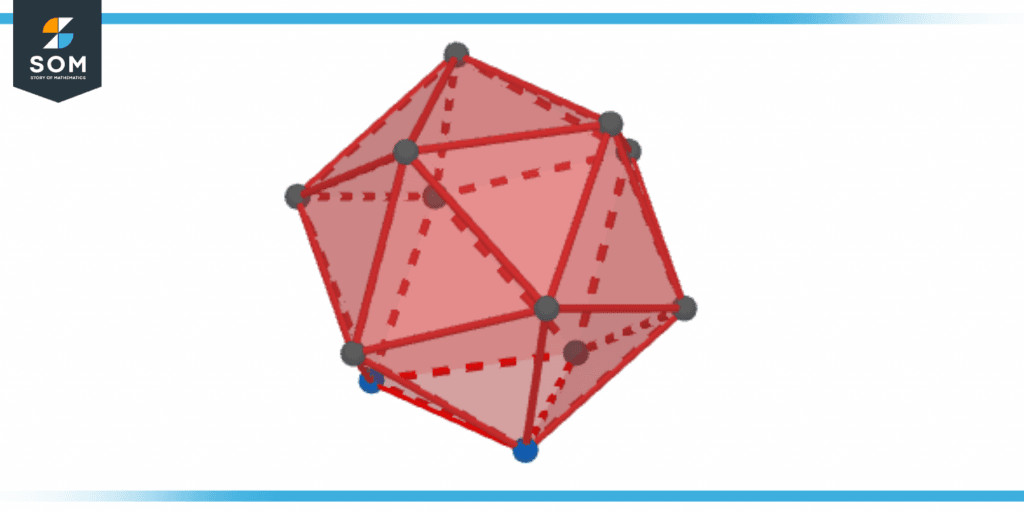
Figure 6 – Regular Icosahedron
- 20 triangular faces
- 12 vertices
- 30 edges
Example 1
A polyhedron with fourteen faces will have twenty edges. What is the total number of vertices that it possesses?
Solution
F + V – E = 2
Where F = Faces, V = Vertices and E = Edges
Given, F = 14 and E = 20
14 + V – 20 = 2
V – 6 = 2
F = 6 + 2 = 8
As a result, the polyhedron has a total of eight faces.
Example 2
A polyhedron has the following dimensions: edges (E) = 6, faces (F) = 8, and vertices (V) = 10. Check to see if there is a polyhedron with all these dimensions.
Solution
Using Euler’s formula, we can apply the following values: E = 6, F = 8, and V = 10
F + V – E = 2
Putting values in formulas:
8 + 10 – 6
12 ≠ 2
Because these values do not fulfill the requirements of Euler’s formula, a polyhedron with the aforementioned number of dimensions doesn’t really exist.
All the figures above are created on GeoGebra.
