Revolution|Definition & Meaning

In the context of mathematics, a rotation of 360 degrees or 2 radians is referred to as a “complete turn” or “revolution.” When studying circles and other circular shapes, this concept is frequently applied in the fields of trigonometry and geometry. 

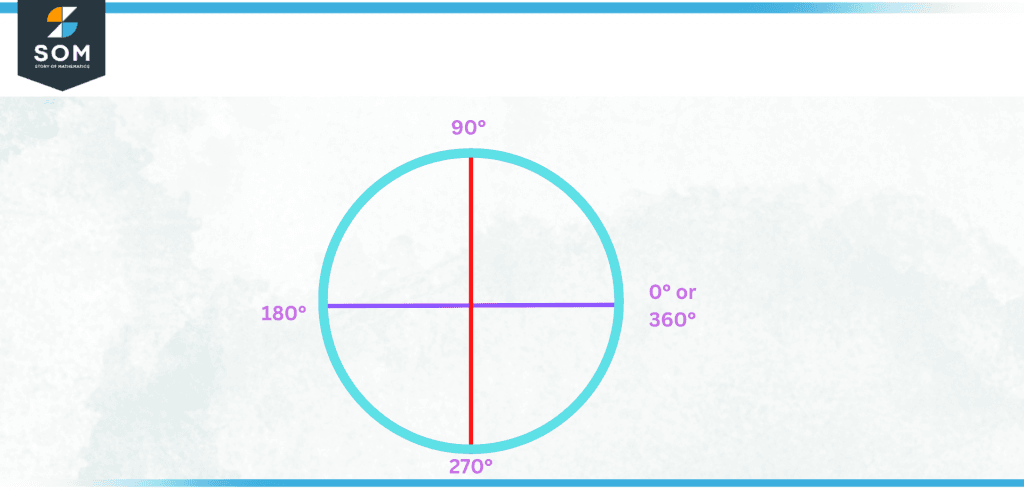
Figure 1 – A circle is composed of 360 degrees.

A “complete turn” can refer to the rotation of an object around a central point in the context of physics. For example, the rotation of a planet around the sun or the rotation of a wheel around its axis are both examples of rotations that can be considered “complete turns.”

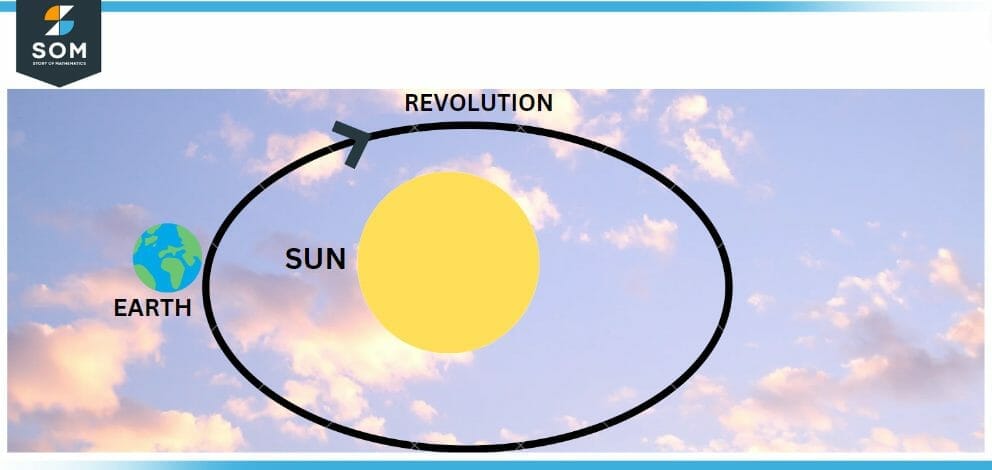
In the field of physics, the term “revolution” can also be used to refer to the movement of a planet or some other celestial body around a central point, such as a star. This type of motion is known as an orbit. The amount of time that must pass for an object to travel around the sun once is referred to as its orbital period. Consider that the orbital period of the Earth is exactly 365 days and 25 hours.

Expressing Rotation in Terms of Degrees

The amount of rotation that anything has been subjected to can be quantified by measuring the number of revolutions in degrees. The number of degrees that make up one complete rotation is equal to 360.

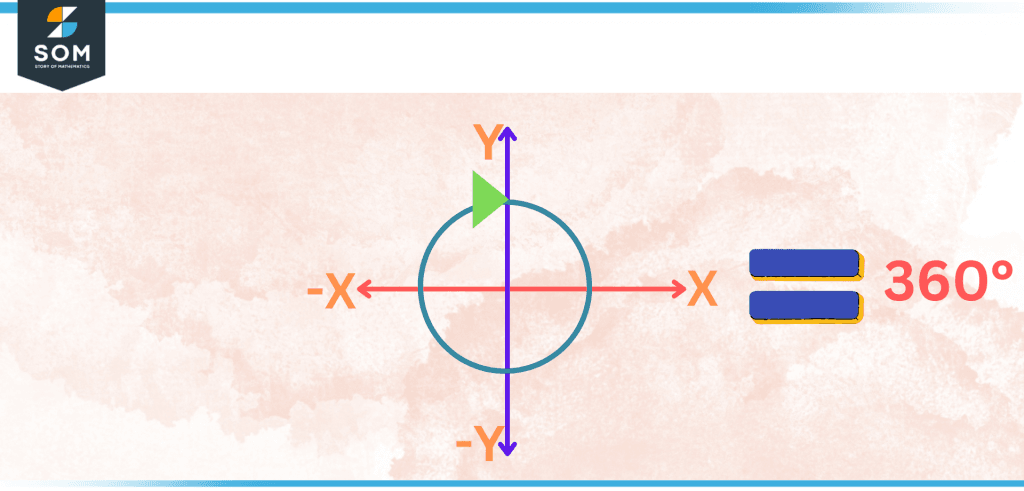
Figure 2 – One revolution is equal to 360 degrees.

Numerous scientific disciplines, including physics, engineering, and astronomy, make use of this measurement. For instance, it is utilized in the field of physics to investigate the motion of various celestial bodies, including planets and satellites, in space.

In the field of engineering, it is utilized for the purpose of measuring the speed and motion of various mechanical components and gears. It is put to use in the field of astronomy for the purpose of analyzing the rotation and orbit of heavenly bodies like planets and stars.

It is vital to measure revolutions in degrees because doing so enables scientists, engineers, and other researchers to quickly compare and study the motion of a variety of different objects.

For instance, if one planet completes one orbit in 365 days and another planet completes one orbit in 600 days, we can immediately understand that the first planet completes more revolutions per day than the second planet does. This is because the 365-day planet has more time to complete one orbit than the 600-day planet.

The degree is the unit of measurement for angles that is used in the SI, which stands for the international system of units. As a consequence of this, it is the unit of measurement utilized all around the world for rotations and angles.

Using Radians as the Unit of Measurement for Revolution

In addition to being measured in degrees, revolutions can also be measured in radians. radians are used more commonly. A radian is a unit of measurement for angles, and one radian is defined as the angle formed by an arc of a circle that has the same length as the radius of the circle. This means that one radian is equal to the angle formed by a circle with a radius of one.

One complete revolution, or 360 degrees, is equivalent to two radians, according to the relationship that exists between degrees and radians. Therefore, 180 degrees is equivalent to the value of radians, 90 degrees is equivalent to the value π/2 radians, and so on.

The radian is the unit of measurement used in the SI system for angles, and it finds particular application in the fields of mathematics, physics, and engineering. For instance, angular velocity is typically measured in radians per second (rad/s) in the field of physics, whereas in the field of engineering, angular displacement is measured in radians.

Utilizing radians has the potential benefit of rendering calculations and equations more intuitive and straightforward to comprehend in some circumstances. There are numerous equations in physics and engineering that are written in terms of radians. Some examples of these include trigonometric functions, which have their definitions expressed in terms of radians.

Both degrees and radians are units of angle measurement, and they can be converted to one another using a straightforward mathematical formula. However, each unit of angle measurement has its own set of benefits and drawbacks, which vary depending on the topic, area of study, and challenge that you are attempting to address. It is important to point this out.

Examples of Evolution in Everyday Life

There are numerous instances of the revolution currently taking place in a variety of fields. Some instances include:

1. The motion of the planets in our solar system is described by the fact that they revolve around the sun. Because it takes the Earth 365 and 24 days to complete one rotation, we have to add a day to our calendar every four years to account for the leap year.
2. Mechanisms, or gears, and machinery: Gears are a common component in mechanical systems because of their ability to transmit both energy and motion. The gears each rotate around their own axis, which in turn causes the rotation of the other gears. The number of rotations that a gear does in one minute, also known as its revolutions per minute (RPM), is a significant measurement of its speed and motion.
3. Turbines: The generators of electricity in power plants are referred to as turbines, and they include both wind turbines and hydroelectric turbines. The output of the turbine can be measured in large part by its revolutions per minute (RPM), which stands for revolutions per minute.
4. Astronomy: In the field of astronomy, another example of revolution is found in the rotation of stars and other celestial bodies. For instance, one revolution around the Milky Way galaxy is completed by the star Polaris, often known as the North Star, in around 434 days on Earth.
5. Technology: When it comes to technology, we have things like CD/DVD players, hard drives, and so on. Because they contain an internal motor that rotates the disc in a circular motion, we need to determine the number of revolutions that they make.
6. Sports: Figure skating, gymnastics, diving, and swimming are all examples of sports in which participants engage in revolutions such as spins and turns. When determining how challenging these maneuvers are to perform and how well they can be done, the number of rotations and the pace at which they are performed are both crucial aspects to consider.
   

   Figure 3 revolution of earth around the sun

Conclusion

In conclusion, having a solid grasp of the idea of revolution is necessary for success in a variety of academic specializations, including physics, engineering, and astronomy. One full revolution is equal to 360 degrees. Hence, the term “revolution” refers to a complete rotation or full turn of an item around an axis.

Revolutions are often measured in degrees, and one full revolution is equivalent to 360 degrees. This measurement makes it possible for researchers, scientists, and engineers to quickly compare and study the motion of various objects, such as planets in orbit around stars or gears in machinery.

It is also important to note that revolutions can also be measured in radians, which is the SI unit of measurement for angles. This measurement system has its own set of benefits and drawbacks, which vary according to the topic, field of study, and difficulty level of the issue that you are attempting to resolve.

Understanding the notion of revolution and being able to measure it in degrees or radians is essential in many fields of study because it enables correct analysis and comparison of the motion of objects. In particular, this is true in the subject of astronomy. This is an elementary idea that is necessary for comprehending a wide variety of physical occurrences.

An Example Involving Revolutions

A wheel with a diameter of 10 centimeters. How much ground has been traversed by a wheel by the time it has completed one complete revolution?

Solution

According to what we know, the distance that a circular wheel with a radius of r travels around a circle during one revolution is equal to the circle’s diameter.

Therefore, the circumference of the wheel is equal to 2πr multiplied by 2πr times 10 cm.

Because of this, the distance it has gone is equal to 20 cm.

All images/mathematical drawings were created with GeoGebra.

Retail Price Definition < Glossary Index > Rhombus Definition