Rhombus|Definition & Meaning

Figure 1 below shows a Rhombus.

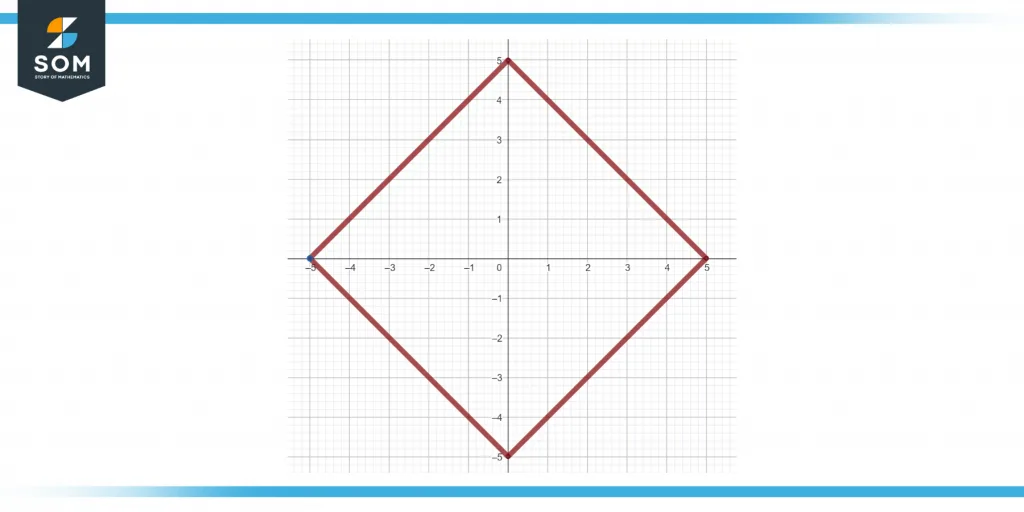
Figure 1 – Representation of a rhombus.

Rhombus as Quadrilateral

A quadrilateral is a rhombus shape. It is a parallelogram with identical sides and diagonals connecting at 90 degrees. This is the rhombus’s most crucial characteristic. A rhombus resembles a diamond. As a consequence, it is sometimes referred to as a diamond. 

A rhombus is a closed planar two-dimensional figure. Due to its distinguishing characteristics, it is classed as an unusual parallelogram and a quadrilateral. Because all of its sides have the same length, a rhombus also was known as just an equilateral quadrilateral.

The term ‘rhombus’ is derived from the ancient Greek term ‘rhombos,’ which refers to something that spins.

A quadrilateral is a closed polygon with four sides and four vertices enclosing four angles. The total of a quadrilateral’s internal angles equals 360 degrees. The quadrilateral is classified into six types:

• Parallelogram
• Rectangle
• Kite
• Trapezium
• Rhombus
• Square

Rhombus, Parallelogram, and Square

A rhombus is a particular parallelogram since it fulfills the definition of a rectangle as a trapezoid with a second pair of parallel sides. A rhombus, like a cube, has four equal sides. As a response, it’s often referred to as a diagonal square. Examine the picture below to see how the rhombus relates to the trapezoid & square.

Figure 2 below shows a difference in Rhombus, Parallelogram, and Square.

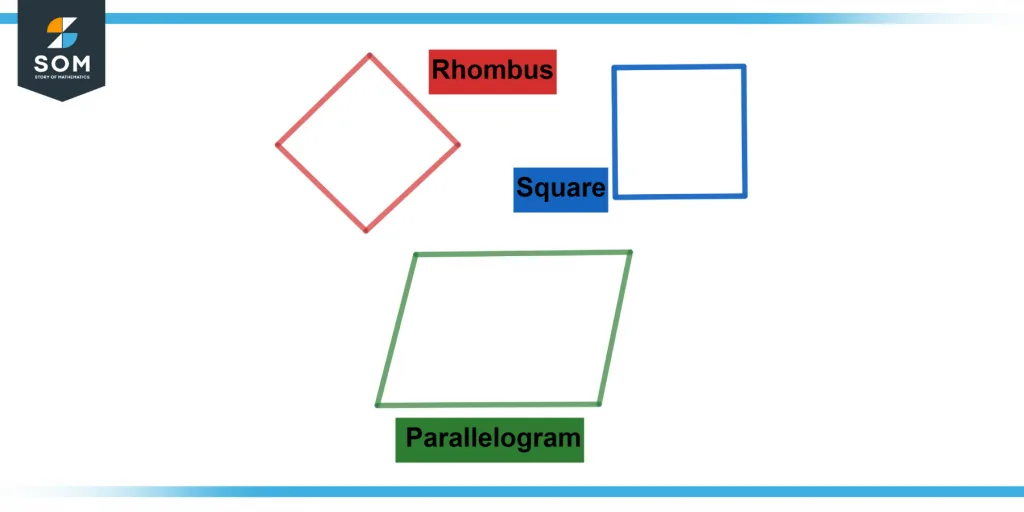
Figure 2 – Difference between a rhombus and other polygons.

Due to its four equal sides, a square is a specific example of a rhombus. All of the angles in a square were right angles. However, not all of the angles in a rhombus must be right angles. As a result, a rhombus containing right angles is a square.

As a result, we may conclude:

Parallelograms are all rhombi or rhombuses, although not all parallelograms are rhombuses.

Every rhombi or rhombus is not a square, but every square is a rhombus.

Three other names can also know a rhombus:

• Lozenge
• Diamond
• Rhomb

Rhombus Angles

One thing to remember regarding a rhombus’ diagonal is that, despite bisecting one another at 90 degrees, the two diagonals crossed will be the same length.

For example, if a diagonal is 10 cm long and another diagonal bisects it, it is split into two 5 cm pieces. You can calculate the length of a diagonal if you know the side of a rhombus and the values of specific angles.

The following are some exciting rhombus angle facts:

• The inner angles of a rhombus are four.
• The total of a rhombus’ internal angles equals 360 degrees.
• A rhombus’s opposing angles are congruent with each other.
• The adjoining angles are extraneous.
• Diagonals in a rhombus intersect at right angles.
• The diagonals of both rhombi bisect these angles.

Figure 3 bellows shows the angles of a rhombus.

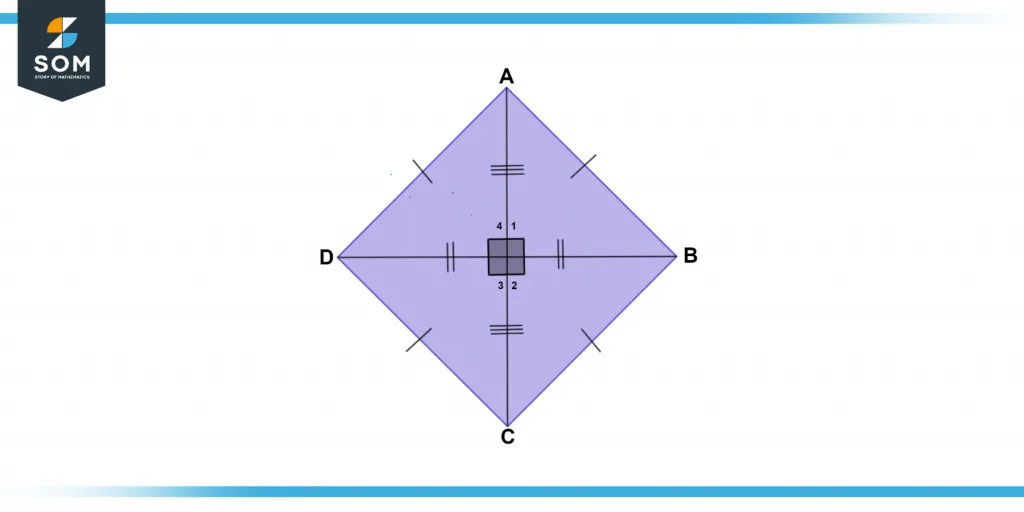
Figure 3 – Representation of rhombus and its angles.

A Rhombus’s Properties

A rhombus is referred to as a unique parallelogram since it possesses all of the features of a parallelogram. Two diagonals serve as symmetry lines in a rhombus.

A symmetrical axis is a distinct line that splits an item in half. It generates a reflecting surface image of the item’s two sides. A rhombus’ diagonals all have reflection symmetry. 

Characteristics of a Rhombus

The characteristics of a rhombus are listed below:

• The rhombus has equal sides on all sides.
• A rhombus’s opposite sides are parallel.
• A rhombus’s opposite angles are equal.
• Diagonals in a rhombus intersect at right angles.
• Diagonals bisect a rhombus’ angles.
• The combination of two angles that are adjacent equals 180 degrees.
• You will receive a rectangle when you link the midpoints of the sides.
• When you combine the center point of half the diagonal, you obtain another rhombus.

There are also a few more advanced properties on its relationships with other geometrical shapes:

• There cannot be a constraining circle around a rhombus.
• There could be no engraved circle within a rhombus.
• The midpoints of four sides will be linked to form a rectangle, and the length and breadth of a rectangle will be the value of a major diagonal, resulting in a rectangle with half the area of the rhombus.
• Two congruent, evenly spaced triangles are generated when the longer diagonal equals one of the sides of a rhombus.
• When the rhombus is rotated around any side as that of the axis of rotation, you will receive a cylindrical surface with a convex conical at one end and a concave cone at the other.
• Whenever the rhombus is rotated about the line connecting the center point of the different sides as that of the axis of rotation, you will see a cylinder surface with concave cones on both ends.
• When the rhombus revolves around the longer lateral axes of rotation, you will get solid with two cones joined to their bases. In this scenario, the greatest diameter of the block is equal to the rhombus’s shorter diagonal.
• When the rhombus revolves around the longer diagonal as that of the axis of rotation, you will get a solid containing two cones linked to their bases. In this scenario, the greatest diameter of the block is equal to the rhombus’s longer diagonal.

The Rhombus Area

The rhombus’ area is the territory it covers in a 2-dimensional surface. The formula for area is the product of the rhombus’ diagonals divided by two. It can be written as:

\[ A = \dfrac{(d1 \times d2)}{2} \times \text{square units} \]

Example of a Rhombus

When they noticed a rhombus-shaped tile, Sam and Victor played hopscotch at the playground. Each side of a tile was ten units long. Can you assist Sam and Victor in determining the tile’s perimeter?

Solution

The tile’s length is ten units.

Because a rhombus has equal sides, all four sides were equivalent to 15 units.

Perimeter = 4, side = 4, ten = 40 units

The perimeter of a tile is 40 units.

All Images are made using GeoGebra.

Revolution Definition < Glossary Index > Rhs Definiton