JUMP TO TOPIC
RHS|Definition & Meaning
Definition
RHS is an acronym for Right Hand Side. In math, this refers to everything on the right side of the equal sign (=) in an equation. When solving equations, we perform a series of mathematical manipulations and operations between the left and right-hand sides to get the result. While it is not a rule, we usually write the final result on the RHS as the last step of the solution.
Right-hand Side
When we have an equation, we are able to split it into two components, which are referred to as the left-hand side and the right-hand side. The left and right-hand sides of an equation are often abbreviated as LHS and RHS.

Figure 1 – RHS of an equation
The term can refer to either an equation or an inequality; the right-hand side of an expression is anything that is located on the right side of a test operator, and the left-hand side (LHS) is defined in the same manner. Note that in mathematics, it is customary to refer to the sides of an equation as “the left-hand side” and “the right-hand side.”
For example, when talking about:
𝑐2=𝑎2+𝑏2
It is more likely that someone will tell you that “the right-hand side is a2+b2” rather than just saying that “the right side is a2+b2.” In mathematical writing, the expressions “right-hand side” and “left-hand side” are frequently abbreviated to “RHS” and “LHS”, respectively.
In a chemical equation, the term “reactant” refers to the material or substances that are located to the left of the arrow. The component that is present at the beginning of a chemical reaction is referred to as a reactant. Products are whichever material or substances may be found to the right of the arrow.
Equations and Sides of Equations
Equations are a type of mathematical statement that contain two algebraic expressions on each side of an “equal to” sign (=) in the middle of the statement. It illustrates the relationship of equality that exists between the expressions written on the left side and the expression written on the right side by placing them side by side.
The left-hand side equals the right-hand side is a condition that must be satisfied in every mathematical equation. Equations can be solved so that the value of a missing variable, which stands for a missing quantity, can be determined.
In a statement, the absence of the symbol for “equal to” indicates that the statement is not an equation. It will be understood that you are making an expression.
If we obtain both the left-hand side (LHS) and the right-hand side (RHS) to have the same value, we may declare that the equation is true; otherwise, we cannot say that the equation is true for at least some values of real numbers.
Example 1: (x + y)2 = x2 + 2xy + y2
Where LHS = (x + y)2 and RHS = x2 + 2xy + y2
Example 2: (x + y)(x − y) = x2 − y2
Where LHS = (x + y)(x − y) and RHS = x2 − y2

Figure 2 – RHS and LHS of an apple
A mathematical equation is a compound expression that consists of two expressions connected by an equals sign, indicating that whatever is written on the left side of the sign is equivalent to whatever is put on the right side of the equals sign. An equation is a mathematical term.
Left-Hand Side (LHS) expression = Right-Hand Side (RHS) expression
This expression can be anything from a single variable to a constant to a polynomial to a logarithmic amount or anything else you can think of.
We have two options at our disposal whenever we need to demonstrate that a given equation or identity is correct: Find the value on one side of the equal sign on one side of the equation using the information from the other side, and if they are equal, the equation is correct.
Simplify both Left Hand Side(LHS) and the Right-Hand side(RHS) until both of them become the same. Then LHS will be equal to RHS, which is written as LHS= RHS, i.e., identity or mathematical approved fact is true.
Simplify the Left Hand Side (LHS) as well as the Right Hand Side (RHS) until they are identical in appearance. Then the LHS will be the same as the RHS, which may be represented as LHS= RHS, which indicates that the identity or mathematically proven fact is correct.
Because one side may be derived from the other using appropriate mathematical processes, the equality sign on the left-hand side of the equation indicates that both sides are equivalent to one another.
Homogeneity of Equations
In the process of solving mathematical equations, in particular linear simultaneous equations, differential equations, and integral equations, the term “homogeneous” is frequently used for equations that have some linear operator L on the left-hand side (LHS) and 0 on the right-hand side (RHS).
In contrast, an equation is said to be inhomogeneous or non-homogeneous if its right-hand side (RHS) does not equal zero, as shown by the following:
Lf = g,
This equation has to be solved in order to find f, given that g is a fixed function. Therefore, a solution to an inhomogeneous equation can have a solution to a homogeneous equation added to it and still be considered a solution to the inhomogeneous problem.
The inhomogeneous equation requires more realistic solutions with some matter or charged particles, whereas the homogeneous equation may correspond to a physical theory that was stated in empty space.
Solving an Equation
An equation can be thought of as a weighing scale in which both sides have the same amount of weight. It does not matter whether we add or remove the same number from both sides of an equation; the result will always be the same.
In a similar vein, even if we multiply or divide the same number into both sides of an equation, the equation will still be correct. Take into consideration the equation of a line, which is 3x minus 2 equals 4.
To maintain the integrity of the equilibrium, we shall conduct mathematical operations on both the left and right-hand sides. Let’s reduce the left-hand side to 3x by adding 2 to both sides. This won’t throw off the equilibrium at all. The new lower horizontal scale is 3x 2 + 2 = 3x, and the new upper horizontal scale is 4 + 2 = 6.
Therefore, the equation may be rewritten as 3x = 6 First, let’s divide both sides by 3, which will bring the left-hand side down to x. Therefore, the answer to the equation that describes a line is x equal to 2.
The following are the actions that need to be taken to solve a fundamental equation with one variable (linear):
The first step is to apply arithmetic operations to both sides of the equation, which will move all of the terms that contain variables to one side of the equation and all of the constants to the other side.
The second step is to combine all like words by adding or removing them. Terms are terms that contain the same variable with the same exponent.
Break it down into its simplest form and get the answer.
An Example of RHS
How many eggs do we have in the given illustration for the RHS? Is the equation correct? If it is incorrect, how would you fix it?
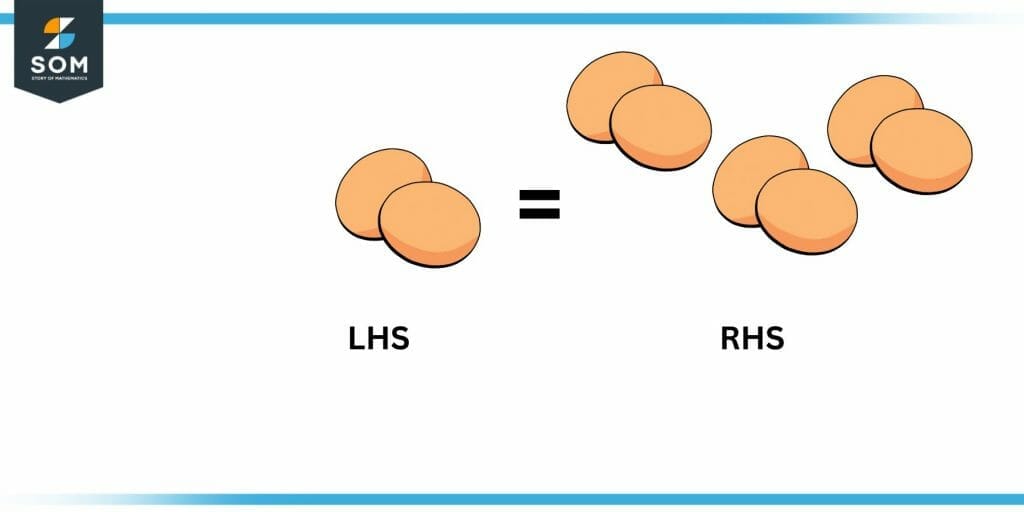
Figure 3 – RHS illustration
Solution
In the given illustration, we have 6 eggs in the RHS. Since 2 eggs on the LHS are not equal to 6 eggs on the RHS, this equation is also incorrect. To fix it, we’d need to add 4 eggs or multiply by 3 on the LHS to balance both the sides.
All mathematical drawings and images were created with GeoGebra.
