JUMP TO TOPIC
Rise|Definition & Meaning
Definition
The difference in the vertical coordinates of any two points on a line is called the rise between those two points if the difference (final point’s ordinate – initial point’s ordinate) is positive. Otherwise, if the difference is negative, it is called the fall. The term represents the numerator of the slope equation, where slope = rise $\div$ run, and rise or fall = y$_f$ – y$_i$.
Rise and Run
The term “rise” refers to the number of units gained or lost by moving from one location to another. That would be represented as a shift in the y values on the graph.
Run is a measurement of how far to the left or right you advance between two points. A graph shift in the x values would show that.
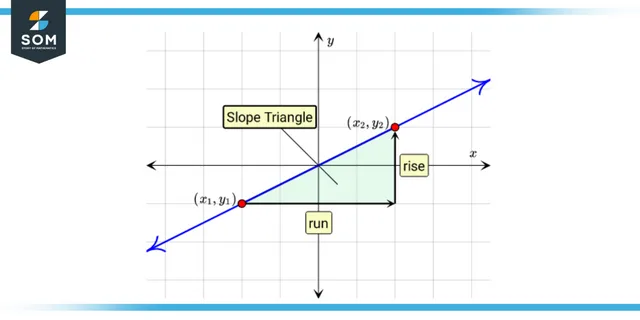
Figure 1: Representation of Rise and Run
Rise Over Run Formula
The “slope formula” for a straight line that joins any two places can also be referred to by its alternative name, the “rise over run formula.” The term “rise” refers to the difference in y-coordinates that can be found between the two sites. The term “run” refers to the difference in the x-coordinates of two points considered to be the same. To get the slope, divide the total elevation gain by the distance traveled.
Steps to Find Rise in Slope
The rise-over-run formula is a valuable tool for determining the slope of a straight line, which can be either positive or negative or equal to zero. The following is a short list of factors that should be kept in mind:
- When the straight line moves from the left to the right and then upward, we say that the line rises and the slope is positive.
- If a straight line slopes downwards while moving from left to right, then the line falls, and the slope of the line is negative.
- If the line is horizontal, there will be no slope because it will be horizontal.
- In the case where the straight line is at an angle, the slope cannot be specified.

Figure 2: Representation of rise over run formula.
Determining Whether the Line Is Positive or Negative
Step 1
On the x-axis, the numbers are written so that they begin to the right of the origin with positive values and progress to the left of the origin with negative values. If the gradient is positive, the line slips uphill from right to left, and the direction of movement is clockwise. The slope is said to be negative if it is sloping in a downhill direction.
In the first step, the equation is transformed into slope-intercept form (y-intercept), and the slope and y-intercept are determined.
It is much simpler to determine the slope of the line and the y-intercept when the information is presented in this fashion.
In this form, the slope is denoted by the letter m, the coefficient placed in front of x, and the y-intercept is denoted by the letter b, which is a constant.
Step 2
The second step is plotting the y-intercept on a graph with two dimensions.
Keep in mind that the point where it crosses the y-axis is where the y-intercept is found. Therefore, the value of x will be 0.
Equations of Lines if you require additional review on intercepts.
Step 3
Determine a second point on the line by making use of the slope.
You will begin at the y-intercept, and depending on the direction of the slope, you will either climb up or down and then run to the left or right.
Determine how to use the slope to get your second point by applying the notion of slope as rise over run (rise/run), which states that slope equals rise over run.
Which of the following represents a positive direction for the rise: up or down? If you answered correctly, pat yourself on the back. That indicates that falling is the opposite direction of rising. Consider that the numbers are on the y-axis as a tool to help you recall this information. The positive values are those located above the origin, while the negative values are those located below the origin.
Right or left, according to you, which do you believe is the better direction to run? If what you say is correct, you should be proud of yourself. That indicates that the left is not a good direction to run in.
Think about the numbers that appear on the x-axis as a technique to help you recall this information. The positive values are represented by moving to the right of the origin, whereas the negative values are represented by moving to the left of the origin.
If the gradient is positive, then the rise and the run must either be positive or negative for the slope to be considered positive overall.
In other words, you will either go up and to the right OR down and the left when you get to this point. Both of these negative directions are valid because the gradient of our slope rises overrun. If you put a negative on top of another negative, the result will always be simplified to positive.
If the gradient is negative, then the rise and the run must be opposites of one other; one must be positive, and the other must be negative for the slope to be negative.
In other words, you will either be heading up and to the left OR down and the right. Both of these directions are possible. If you make them both negative, it will simplify to be positive, and you will have an erroneous graph. You want to avoid doing this since it will cause the graph to be incorrect.
You should also remember that there is a denominator or run of your slope if the slope you are working with is a non-zero integer, such as -5 or 10. What does it mean for an integer to have a denominator that is not zero? If you said 1, you are correct!!!
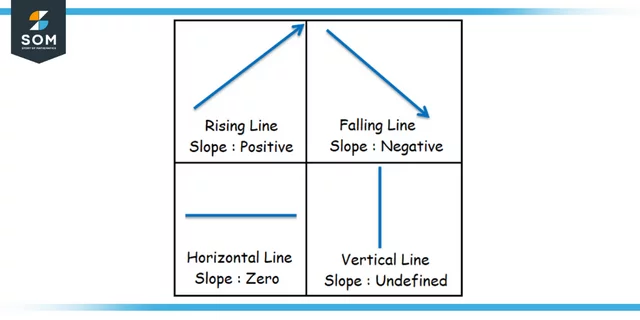
Figure 3: Representation of different slopes.
Step 4
Connect the spots found in stages 2 and 3 with a line you draw.
Examples of Rise
Example 1
If point A (0,5) and B (2,9) then by using rise-over-run formula determine the slope (m) of the line. And write the equation of the line in the standard form too.
Solution
The formula of slope (m) is given as
m= (y2−y1) / (x2−x1)
= (9 – 5) / (2 – 0)
= 4 / 2
= 2
Using the slope-intercept form, the equation of this line can be written as:
y = mx + c
y = 2x + c
Point (0, 5) passes through the line, so substituting x = 0 and y = 5 in the above line equation, we will get:
5 = 2(0) + c
c = 5
Therefore, the line equation is y = 2x + 5.
Converting the line into the standard form:
y = 2x + 5
Subtracting y on both sides, we get:
2x – y + 5 = 0
Subtracting 5 on both sides, we get:
2x – y = -5
The above equation is the Standard Form. Thus, 2 is the slope of line joining A and B.
2x – y = -5 is the standard form of line equation.
Example 2
A square has four sides one of its corner point is X (2,2). If the sides of the square are parallel with their x-axis and y-axis, given that the square lies in the first quadrant. Determine the slope of both diagonals of the given square.
Solution
x-coordinates of X and Y will be same because the line which is joining X and Y is parallel to the y-axis
X = (2, 2) Y = (2, y)
The total distance between X and Y points is 4 units.
By using the distance formula we will get:
XY = 4 = [(2 – 2)2 + (y – 2)2]1/2
y = 6
Therefore coordinates of Y are (2, 6).
Similarly, the coordinates of C are (6, 6), and the coordinates of D are (6, 2).
The slope of both diagonals of the square is m1 and m2, respectively. Let us find them using the rise-over-run formula.
For (m)1:
= 6 – 2/ 6 – 2
= 1 (for the diagonal AC)
For (m)2:
= 6 – 2/ 2 – 6
= -1 (for the diagonal YD)
Therefore, the slopes of both diagonals are:
(m)1 = 1 and (m)2 = -1
Example 3
If point C (2,6) and D (4,8) then by using rise-over-run formula determine the slope (m) of the line.
Solution
Using the rise over run formula, we will first get the slope:
Slope (m) = y2 – y1/ x2 – x1
= 8 – 6/ 4 – 2
= 2/2
= 1
Example 4
Determine the slope of the line 6x + 4y = 12.
Solution
y = mx + c (m is the slope)
To get the slope, subtract 6x on both sides:
6x + 4y – 6x = 12 – 6x
4y = -6x + 12
Now divide by 4 on both sides:
4y/4 = -6x/4 + 12/4
y = -3/2x + 3
In the above, m = -3/2 is the slope.
All images/graphs are created using GeoGebra.
