JUMP TO TOPIC
Root | Definition & Meaning
Definition
When dealing with functions, the root represents the value(s) of the variable where a function evaluates to zero. For example, the root of f(x) = x – 2 is x = 2, since f(x = 2) = 2 – 2 = 0. In some advanced contexts, roots are called zeros to avoid confusion with radicals (square roots, cube roots, etc., which are different things entirely).
What Is a Root?
A function‘s root is the variable‘s value that satisfies the equation when the function itself equals zero. This concept helps to find the roots of the equation, and it becomes easier to solve the equation further. The roots of a function are also called zeros of a function.
Roots can be found algebraically as well as graphically. The fundamental theorem of algebra shows that the number of roots of a polynomial function gives the degree of the polynomial.
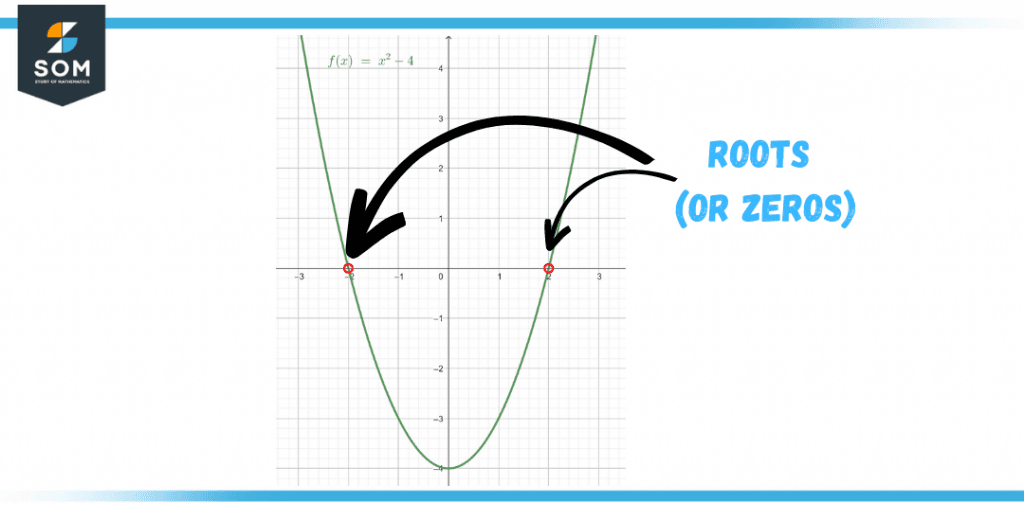
Figure 1 – Roots of a simple quadratic equation
How To Find the Roots of a Function?
It is a simple method to find roots of any type of function, whether it is a linear, quadratic, rational, or logarithmic function. To find the roots of a function, we isolate x on one side of the equation and manipulate the equation for the roots.
The function whose degree is 1 is called a linear function or linear polynomial, e.g., 5x – 4.
The function whose degree is 2 is called a quadratic function or quadratic polynomial, e.g., x2 + 4x + 3.
The function of degree 3 is called a cubic function, e.g., 2x3 + x2 – 13x + 6 is a cubic function.
Similarly, 16x7 + 6x4 – 3x2 is a polynomial/function of degree 7.
There is a different method for finding roots of different degrees of functions.
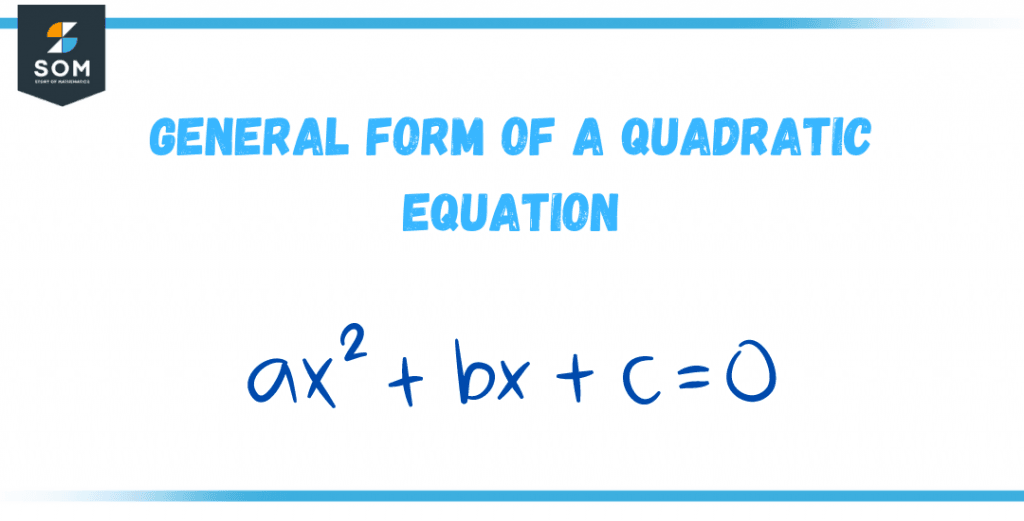
Figure 2 – General form of a quadratic equation
Roots of a Linear Function
Root/zero of a linear function is the value of the independent variable when the dependent variable is kept zero, i.e., if an equation has variables x and y, then y will be the dependent variable and x will be the independent variable, but if the equation has variable other than x and y then the one plotted on vertical axis would be dependent.
To find the zero of the linear function, first, we need to identify the dependent and independent variables. Then substitute zero for the dependent variable, and hence it will drop out of the equation of the function. Since the dependent variable has now vanished, the equation can be solved for the remaining variable, and the solution would be the root of the equation of the function.
Roots of a Quadratic Function
Following are the methods to find the roots of a quadratic function
- Completing square method
- Middle-term break method
- Using the quadratic formula
Completing Square Method
Consider a quadratic equation:
ax2 + bx + c = 0
Rewrite it in the form as:
ax2 + bx = -c
Divide the constant a into both sides if a is not equal to 1. Now the equation becomes:
x2 + $\dfrac{bx}{a}$ = – $\dfrac{c}{a}$
Divide the x term coefficient, i.e., $\left(\dfrac{b}{a}\right)$ by 2 and it becomes $\left(\dfrac{b}{2a}\right)$.
Square it $\left(\dfrac{b}{2a}\right)^2$ and add it to both sides of the equation, now the equation becomes:
x2 + $\dfrac{bx}{a}$ + $\left(\dfrac{b}{2a}\right)^2$ = – $\dfrac{c}{a}$ + $\left(\dfrac{b}{2a}\right)^2$
The left side of the equation can be written as:
$\left(x + \dfrac{b}{2a}\right)^2$
which is the perfect square.
The equation becomes:
$\left(x + \dfrac{b}{2a}\right)^2$ = -$\dfrac{c}{a}$ + $\left(\dfrac{b}{2a}\right)^2$
Now take the square root on both sides and solve for the value of x. The solution will be the root of the equation.
Middle-term Break Method
Consider a quadratic equation ax2 + bx + c = 0 (a = 1). In this method, we split the coefficient of x. Think of 2 numbers such that their sum will be equal to b and their product will be equal to c. now factorize the values and make a pair of expressions.
Equating each expression one by one with zero and extracting out the values of x will give the roots of the quadratic equation. Since it is an equation of degree 2 so we will get 2 roots.
Using Quadratic Formula
Consider a quadratic equation ax2 + bx + c and take the values of coefficients of x2, x, and constant. Put these values in the quadratic formula, and the solution will be two roots of the quadratic equation.
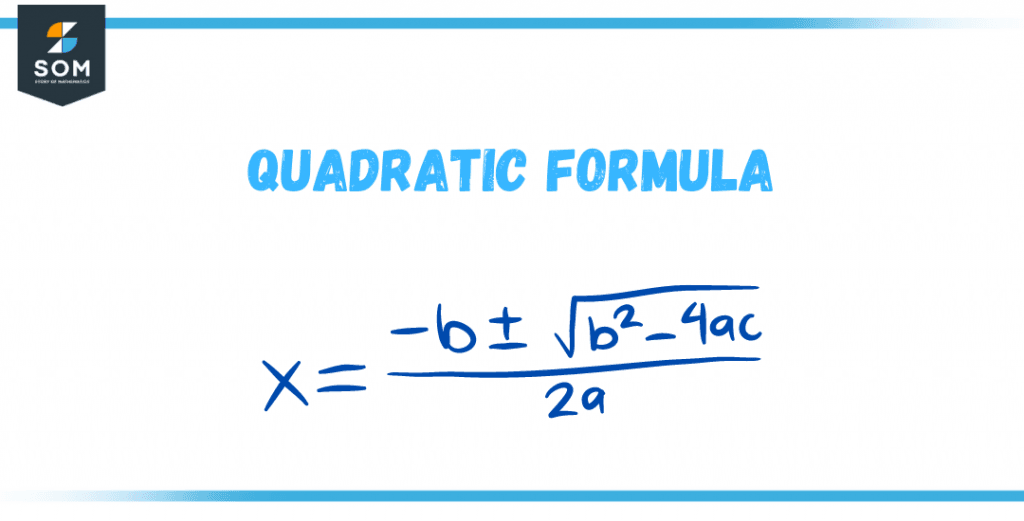
Figure 3 – Quadratic Formula
Nature of Roots of Quadratic Equation
The nature of roots can be specified by finding the value of discriminant D.
Discriminant = D = b2 – 4ac
If the value of D is greater than zero, i.e., D>0, the roots are real and distinct.
If the value of D is equal to zero, i.e., D=0, the roots are real and equal.
If the value of D is less than zero, i.e., D<0, the roots are imaginary.
Roots of a Cubic Function
The roots of a cubic function can be found by factorizing the given equation into a linear or quadratic equation. Further, the quadratic or linear equation can be solved by any of the methods discussed above.
Cubic polynomials can be factorized by the synthetic division method and remainder theorem.
Remainder Theorem
In the remainder theorem, guess the value for the variable, i.e., x. Let us put x = a, y becomes zero; hence (x – a) is a root of the cubic polynomial. Then we divide the cubic polynomial with the root (x – a) by long division to obtain a quadratic equation. Further, this quadratic equation can be solved by any of the three methods to solve a quadratic equation.
Synthetic Division Method
In the synthetic division method, guess the value of the variable which satisfies the equation (same as in the remainder theorem). Then write the coefficients of all the variables in descending order and put zero if any of the terms are missing.
Now bring the first term down, multiply it with the value of the root or divisor, and write it down under the next term. Now add both the values and write the answer at the bottom of the row. Repeat the step 3,4 times or as required until you reach the end of the problem. You will get a quadratic equation that can be easily solved further to find the roots.
Roots of Higher Degree Functions
Roots of higher-degree polynomials can also be found by the remainder theorem and synthetic division method to get a quadratic equation, and it can be further factorized to find the roots.
Solved Example of Finding Roots
Find the roots of the following equations
$\dfrac{x}{2}$ + 3 = 7
x2 – 5x + 6 = 0
x3 + x2 – x – 1 = 0
Solution
Part 1
$\dfrac{x}{2}$ + 3 = 7
$\dfrac{x}{2}$ = 7 – 3
$\dfrac{x}{2}$ = 4
x = 4*2
x = 8
Hence 8 is the root of the equation.
we can also check if the answer is correct or not by putting the answer in the given equation as
$\dfrac{8}{2}$ + 3 = 7
4 + 3 = 7
7 = 7
The equation is satisfied; hence it is confirmed that 8 is the root.
Part 2
Given x2 – 5x + 6 = 0
Using the middle–term break rule,
x2 – 2x – 3x + 6 = 0
x(x – 2) – 3(x – 2) = 0
(x – 3)(x – 2) = 0
Check
Put x = 3 in the given equation.
(3)2 – 5(3) + 6 = 0
9 – 15 + 6 = 0
0 = 0
Put x=2 in the given equation.
(2)2 – 5(2) + 6 = 0
4 – 10 + 6 = 0
0 = 0
Hence, x = 2 and x = 3 are the roots of the equation.
Part 3
Given x3 + x2 – x – 1 = 0
Using synthetic division, let x = 1 and put it in the equation
(1)3 + (1)2 – 1 – 1 = 0
1 + 1 – 1 – 1 = 0
2 – 2 = 0
0 = 0
x=1 is the root of the equation, which can be used in synthetic division.
All images are created using GeoGebra.
