JUMP TO TOPIC
Rotational Symmetry|Definition & Meaning
Definition
A figure which becomes identical to itself after rotation through some angel is said to have rotational symmetry. For some figures, the rotation must be through a certain angle e.g., a 90 degrees rotation for a Square produces identical figure. However, for a circle and ellipse – rotation through any angle produces a identical figure and thus have rotational symmetry for all.
In your day-to-day life, you have probably come across the word “symmetrical” very frequently. It is a symmetrical and comparable resemblance seen in two halves of a figure. That is, one part is the replica of the other part. In other words, it is a similarity that is discovered in an object’s halves.
A shape is said to be asymmetrical if it does not exhibit symmetrical balance across its entirety. There are many examples of symmetry all around us, including in nature, architecture, and art. It is possible to investigate it when you move, rotate, or twist an object. There are many possible varieties of symmetry, including the following:
- Reflection symmetry
- Translational symmetry
- Rotational symmetry
Rotational Symmetry
A figure is said to have rotational symmetry of order “n” if it can be turned by 360°/n and maintain the exact same appearance as the figure it started out as after the revolution. In this context, n is a positive integer that stands for the number of times the image can be spun while maintaining its original appearance in its entirety.
An image with rotational symmetry of order 4 has, for instance, four unique orientations that become indistinguishable from one another after the figure is rotated by 360 degrees plus four quarters, which equals 90 degrees.
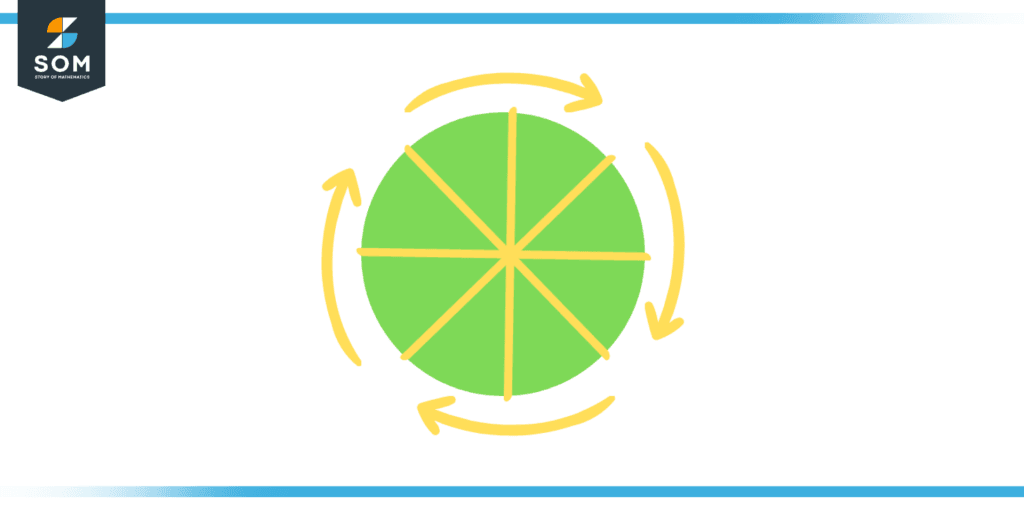
Figure 1: Illustration of Rotational Symmetry
Utilizing transformation theory allows for the definition of rotational symmetry from a purely mathematical perspective. A rotational transformation is a linear transition that maps one set of points in a two-dimensional surface towards another collection of points by turning the first group of points around a fixed point, which is referred to as the center of rotation.
A figure is said to have rotational symmetry if it is unaffected by a rotational transformation—that is, if it is unaltered after the transformation—and if it can be rotated without changing its shape.
Types of Rotational Symmetry
There are three different kinds of rotational symmetry, which are as follows:
Point Symmetry
Point symmetry, often referred to as central symmetry or origin symmetry, is a kind of rotational symmetry in which a figure retains its appearance even after being rotated around a central point by an angle of 180 degrees. The term “center of rotational symmetry” refers to this central location in the structure.
One example of point symmetry is the shape of a heart, which retains its appearance even after being rotated about its center by an angle of 180 degrees.
Line Symmetry
Line symmetry also referred to as axial symmetry or reflectional symmetry, is a kind of rotational symmetry in which a figure retains its appearance after being reflected along a line. Other names for line symmetry include reflectional symmetry and axial symmetry. The axis of symmetry refers to this particular line in the diagram.
For instance, the letter “X” has line symmetry since it retains its appearance regardless of which of its diagonals it is reflected across.
Plane Symmetry
Plane symmetry also referred to as translational symmetry or complete symmetry, is a kind of rotational symmetry in which a figure retains its appearance even after being turned 360 degrees around a central point and, if required, translated back to its initial position.
Other names for this type of symmetry are entire symmetry and full translational symmetry. The term “center of rotational symmetry” refers to this central location in the structure.
For instance, a circle possesses plane symmetry because it retains its shape even after being rotated around its center by a full 360 degrees.
Measuring Rotational Symmetry
The measurement of rotational symmetry requires an understanding of two fundamental ideas: The order of rotational symmetry and the angle of rotation.
Order of Rotational Symmetry
The number of times that a shape may be rotated while maintaining an appearance that is identical to the original form is referred to as the order of rotational symmetry.
The ratio of 360 degrees to the angle of rotation is what constitutes the order of rotational symmetry; more specifically, the order of rotational symmetry is equal to 360 degrees divided by the angle of revolution.
A figure with rotational symmetry of order 4 has, for instance, four unique orientations that become indistinguishable from one another after the figure is rotated by 360 degrees plus four quarters, which equals 90 degrees.
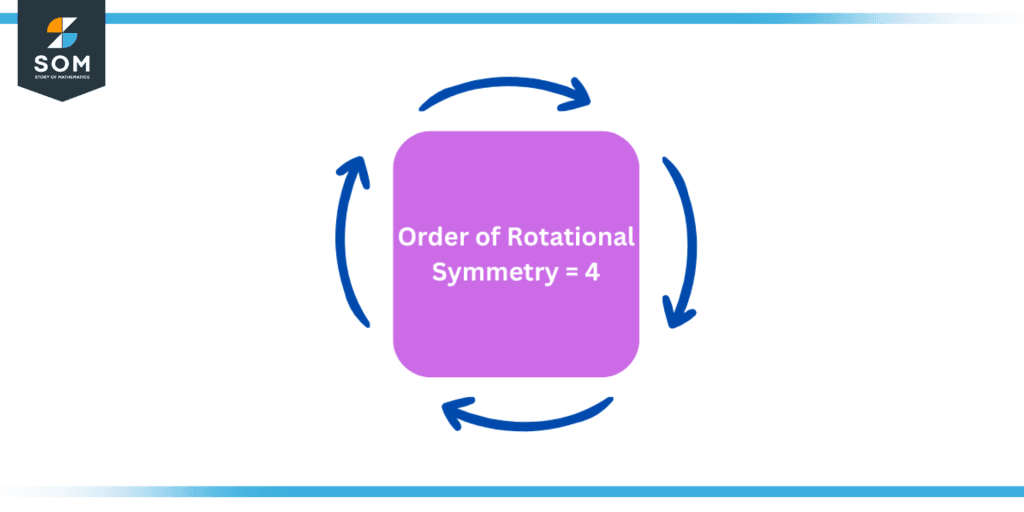
Figure 2: Rotational Symmetry of a Square
Angle of Rotation
The degree to which a figure must be turned in order to produce an image that is identical to the figure’s initial representation is referred to as the angle of rotation. Because it establishes the order of rotational symmetry, the angle of rotation is an essential parameter in the process of determining rotational symmetry and measuring it.
A circle, for instance, exhibits plane symmetry since it retains its appearance even after being turned by an angle of 360 degrees about its center, and thus angle of rotation for a circle is 360 degrees. The following procedures can be carried out in order to determine whether or not a figure possesses rotational symmetry:
- First, sketch out the figure and then locate the center of rotational symmetry for it.
- Give the figure a particular amount of rotation and then examine how it differs from the first figure.
- Continue rotating the figure at a similar angle until it has the exact same appearance as the first version of the figure.
- Make a note of the number of times the figure needs to be rotated before it yields the same result as the first time.
- Determine the angle of rotation by taking the requisite number of rotations and dividing that number by 360 degrees.
Applications of Rotational Symmetry
There are a number of essential uses for rotational symmetry in a variety of domains, including the following:
Art and Design
In the fields of art and design, rotational symmetry is frequently employed as a method for developing compositions that are both aesthetically beautiful and balanced. Designs and layouts that have a feeling of equilibrium and symmetry can be created by artists and designers through the utilization of rotational symmetry.
For instance, a mandala is a spherical design with rotational symmetry that is employed in a variety of artistic expressions and meditation practices.
Biology
In the field of biology, the structure of organisms and the parts that make up their bodies is often described using a concept called rotational symmetry. In biology, rotational symmetry can be seen in the form of things like the spiral structure of seashells and the radial symmetry of sea anemones, for instance.
Physics
In the field of physics, rotational symmetry is a way to characterize the symmetries that are present in physical systems as well as the physical laws themselves. For instance, the rotational symmetry of a molecule is what decides the properties of the molecule, both chemically and physically.
Rotational symmetry is the foundation for many of the principles that govern physics, including the principle of conservation of angular momentum.
Mathematics
In the field of mathematics, rotational symmetry is applied in geometry and topology to investigate the characteristics of geometric figures and the ways in which they can be transformed. The study of groups, symmetries, and various other complicated mathematical concepts necessitates the utilization of rotational symmetry.
Computer Science
In the field of computer science, image analysis, and computer animation are two applications that make utilization of rotational symmetry. The rotational symmetry principle is used, for instance, in the computation of algorithms for spinning and resizing images.
Example of Rotational Symmetry
Find the order of symmetry of an equilateral triangle.
Solution
As we have discussed above that the order of symmetry of any geometrical figure is the number of times that a shape may be rotated while maintaining an appearance that is identical to the original form. Now we will calculate the order of symmetry of an equilateral triangle by considering the following diagram.
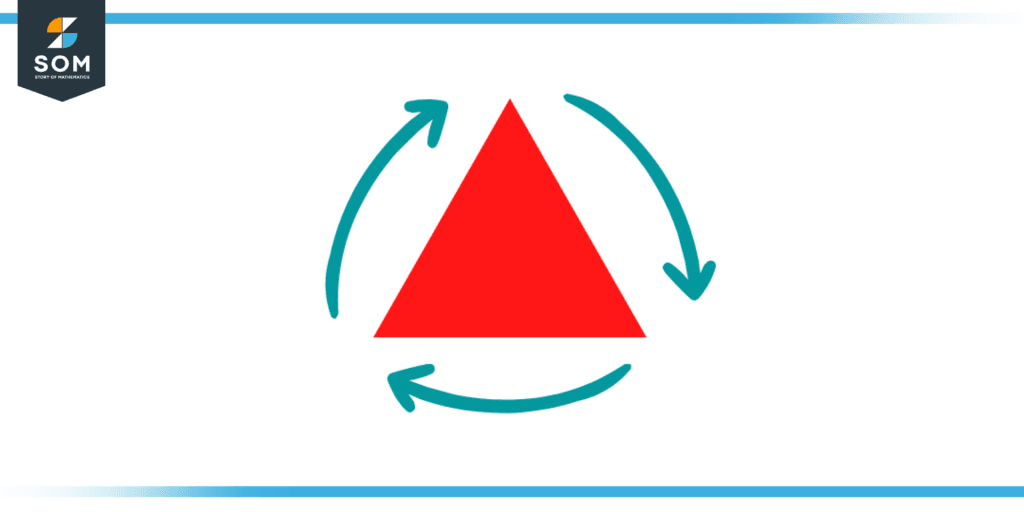
Figure 3: Rotational Symmetry of Equilateral Triangle
As we can clearly see from the above picture that the equilateral triangle can be rotated thrice while retaining its original shape and form.
Thus, the order of symmetry of an equilateral triangle is three.
All images/mathematical drawings were created with GeoGebra.
