JUMP TO TOPIC
Row|Definition & Meaning
Definition
In mathematics, a row is a general term describing things that lie horizontally adjacent (left-right) to each other. This is contrary to columns, which describe things lying vertically adjacent (up-down) to each other.

Figure 1: A row of eleven circles
A row refers to the way that items can be arranged. Although rows and columns are frequently combined to make arrays, this is not required; rows and columns can exist independently. Most often, rows and columns are perceived as horizontal and vertical, respectively.
However, this is mostly just a standard practice because, depending on your point of view, you may rotate something so that the framework that was previously in the form of a row would now be a column according to how you interpret horizontal or vertical.
Common Examples of Row in Real Life
The seats are frequently arranged in rows in places like stadiums, cinema halls, sports facilities, or anywhere else where structured seating can be useful. It is typical to have rows with labels that include both numbers and letters. For instance, the seat number “B3” on your ticket can relate to row B, seat 3.
Rows of plants, trees, or crops are frequently seen in daily routine life. Rows of crops on a farm may be visible, as well as rows of trees placed alongside the road. You might even have rows of plants within your own backyard.
In the database, the columns hold information on the people you are addressing in the rows, whereas the rows themselves contain data such as name, gender, and other attributes.
The fact that rows can serve as a pretty practical approach to arranging objects in a straightforward, ordered fashion is one factor that explains its convenience.
Difference Between Rows and Columns
Following are some factors that help in differentiating rows and columns.
- A row is a group of items arranged horizontally or beside one another. A vertical grouping of items based on type is known as a column.
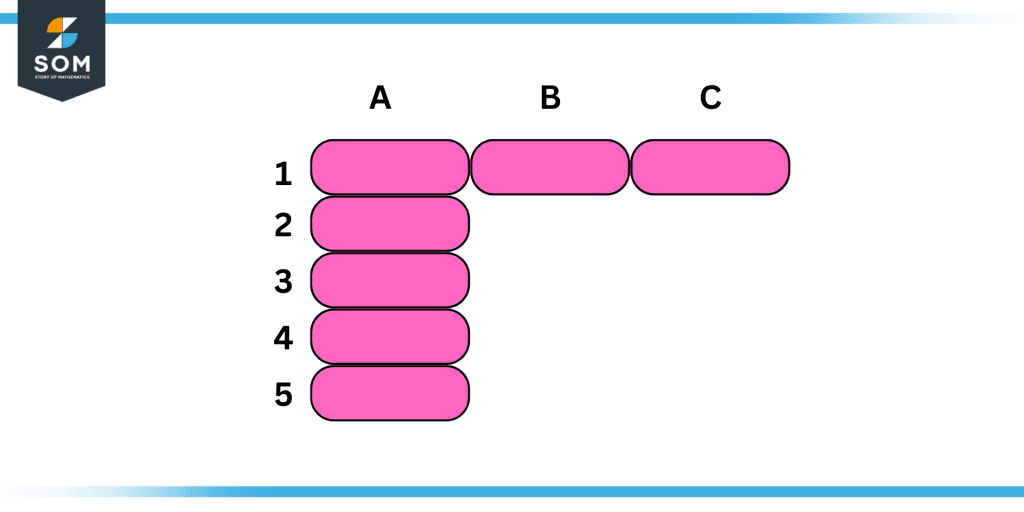
Figure 2: Difference between rows and columns
- In the case of rows, the configuration is from left to right. In the case of columns, the configuration is top to bottom.
- In rows, the total of an arrangement is displayed very right. But in b, the very bottom displays the total.
- The row is described by a stub, which is the very leftmost element of the table. The column is described with a caption that appears in the table’s top row.
- Rows are the term for the horizontal arrays in a matrix, whereas the vertical arrays in a matrix are called columns.
- Numbers are typically used to identify row heads. Alphabets are used to identify column heads.
Row Matrix
A row matrix in mathematics is a kind of matrix that only has one row. However, a row matrix may have more than one column. So, if the matrix has a dimension of (1 x n) or greater, it is called a row matrix.

Figure 3: A row matrix of the order 1×6
The elements are set up so that each row within the matrix is represented by one arrangement of elements.
We cannot determine the determinant of a row matrix simply owing to the fact that it is not a square matrix. We can only calculate the determinant if the order of the row matrix is (1 x 1), which means that both the number of rows and columns equate to b.
Properties of a Row Matrix
The properties of a row matrix are as follows:
- One row makes up a row matrix.
- There are many columns in a row matrix.
- In a row matrix, the number of columns matches the number of entries in the matrix.
- A horizontally aligned, rectangular array of items is called a row matrix.
- A column matrix is created by transposing a row matrix.
- A row matrix can only be added to or subtracted from using another row matrix of the same order.
- Only when there is the existence of a column matrix is it possible to multiply a row matrix.
- A singleton matrix is produced when a row matrix and a column matrix are multiplied.
Rows in MS Excel
A row is a collection of cells arranged in a horizontal, straight line in Microsoft Excel. Both the concepts of rows and columns form the basic structural definition of MS Excel.
Microsoft Excel is used for a variety of purposes, from calculating complicated mathematical formulations to making forecasts, spending and tracking budgets, and simplifying and organizing data analysis.
Examples – Illustrating the Concept of Rows
Example 1
The following shows an array of 0s. Assess it and find out the number of rows, columns, and the total number of 0s.
000000000000
000000000000
000000000000
000000000000
Solution
The number of rows in the above array is 4.
In a similar fashion, we can assess just by looking at the array that there are 12 columns present in the array.
To find out the total number of zeros in the above array, we will use the following formula:
No. of 0s = m x n
Where:
m = no. of rows
n = no. of columns
Therefore:
No. of 0s = 4 x 12 = 48
Hence, there are 48 zeros that constitute the above array.
Example 2
The following are two-row matrices, A and B.
A = [2 4 6 8 10]
B = [3 5 7 9 13]
Add both matrices. Also, mention the order of matrix A, matrix B, and the result of their sum.
Solution
To add two matrices, we just sum the corresponding entries.
As:
A = [2 4 6 8 10]
B = [3 5 7 9 13]
Their sum would be Z:
Z = A + B
= [2 4 6 8 10] + [3 5 7 9 13]
Z = [5 9 13 17 23]
The result of the addition of row matrices is always another row matrix.
The order of a matrix is described by (m x n), where m is the number of rows while n is the number of columns.
Since:
A = [2 4 6 8 10]
Order of A = 1 x 5
Similarly, for B and their sum Z:
B = [3 5 7 9 13]
Order of B = 1 x 5
Z = [5 9 13 17 23]
Order of Z = 1 x 5
All images/mathematical drawings were created using GeoGebra.
