JUMP TO TOPIC
Run|Definition & Meaning
Definition
The difference in the vertical coordinates of any two points on a line is called the rise between those two points if the difference (final point’s ordinate – initial point’s ordinate) is positive. Otherwise, if the difference is negative, it is called the fall. The term represents the numerator of the slope equation, where slope = rise $\div$ run, and rise or fall = y$_f$ – y$_i$.
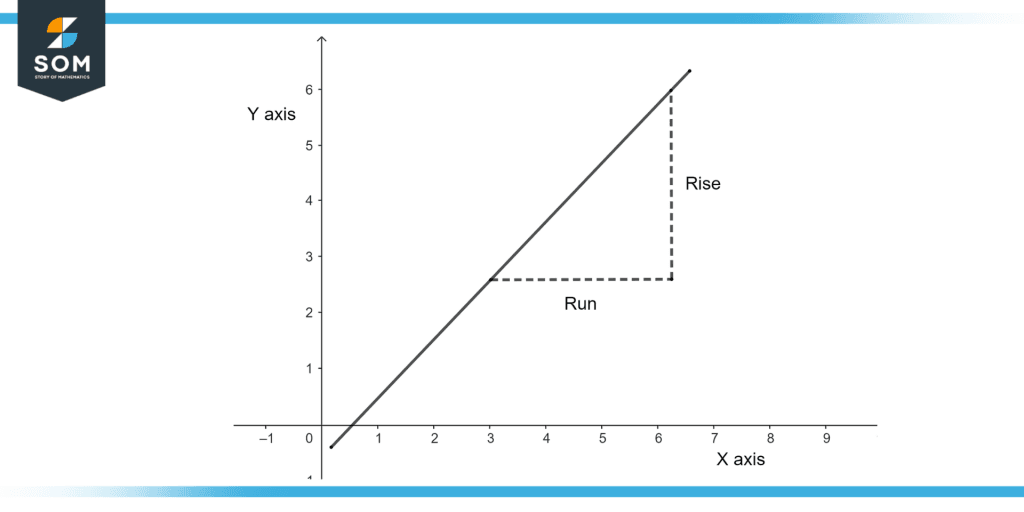
Figure 1 – Rise and Run of Line
Figure 1 illustrates the rise and run of a straight line.
The formula describing the “slope” of a straight line connecting any two locations is known as the rise over run formula. The term “rise” refers to the variation in the y-coordinates between two places. The term “run” refers to the variation in the x-coordinates of two identical places.
Slope of a Line
In daily life, you frequently come across the concept of slope. Consider descending a slope with a cart or ascending some steps. There is a slope on the steps as well as the ramp. By taking both horizontal and vertical movement along the ramp and steps into account, you may define the slope, or steepness, of those features. In conversation, you characterize slope with “gradual” or “steep.”
Most of the movement is horizontal down a gradually inclining slope. The vertical movement is larger when the slope is steep. The concept of slope in mathematics is pretty close to how we normally define it.
Simply put, the slope is both a literal and mathematical term used to indicate a line’s steepness and direction. A line’s slope can be inferred from its graph alone, especially in relation to other lines shown on the same coordinate plane.
As x rises, y rises, or alternatively, when x falls, y falls visually. This indicates that as we travel from left to right on the graph, the line rises, and the slope is positive. If, on the other hand, as x rises, y falls, or alternatively, when x falls, y rises, then as we travel from left to right on the graph, the line descends, and the slope is negative.
As x rises, y remains constant, or alternatively, y remains constant while x falls as we travel from left to right on the graph, the line does not move up or down, visually indicating that it is horizontal and a constant function then the slope is zero. If y takes on any value and x takes on only one value visually, this means the line is fully vertical, and the slope is undefined.
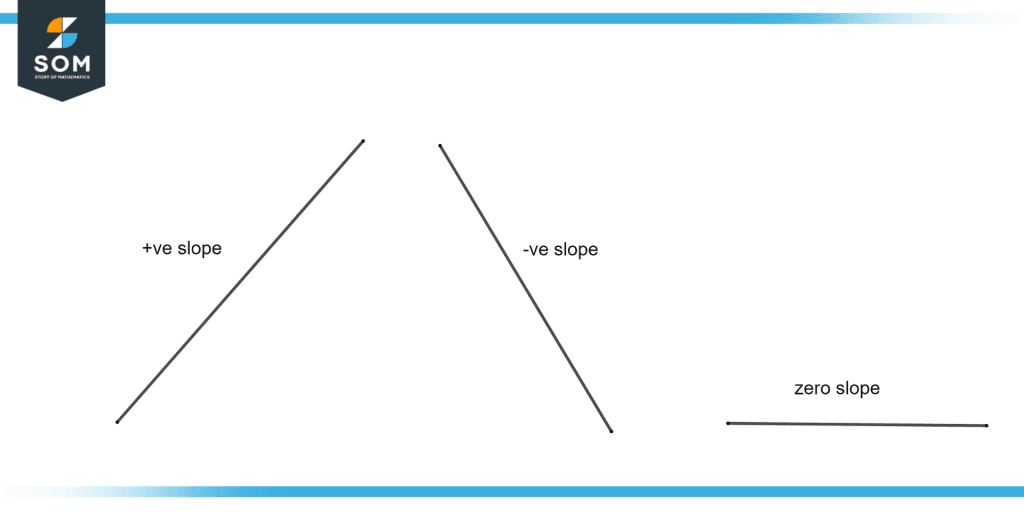
Figure 2 – Positive, negative, and zero slope
Figure 2 illustrates the positive, negative, and zero slopes of a straight line.
Rules for Implementation of Rise Over Run Formula
The slope of a straight line, which can be negative, positive, or zero, can be calculated using the rise-over-run formula. Remember the following main points:
- If a straight line is heading up and from left to right, it is a rising line with a positive slope.
- If a straight line is falling with a negative slope if it is moving downhill and from left to right.
- The slope of a straight line will be 0 if it is horizontal.
- The slope is unclear whether the straight line is vertical.
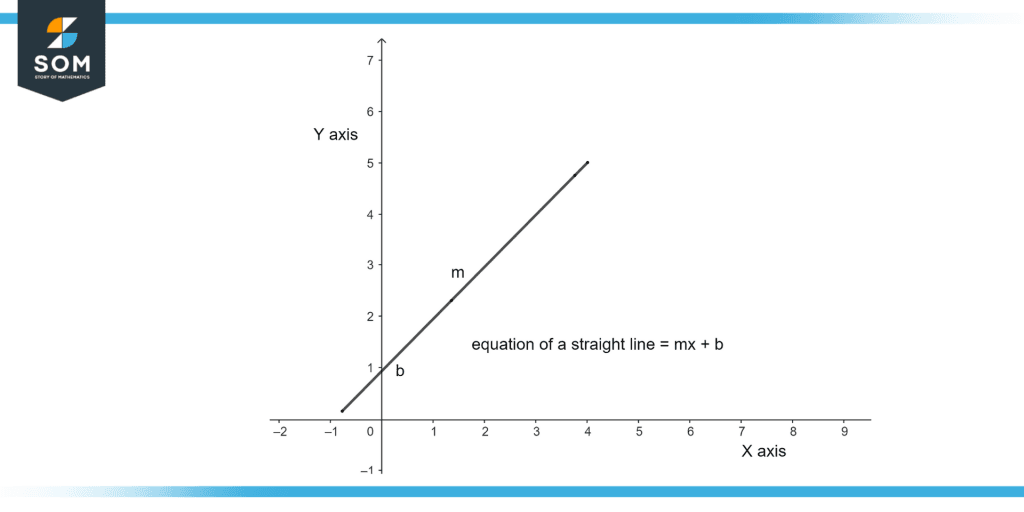
Figure 3 – Equation of a Straight Line
Figure 3 illustrates the equation of a straight line in which m indicates the slope or gradient while b indicates the y-intercept.
The slope formula is as follows if $U(x_1,y_1)$ and $V(x_2,y_2)$ are the two points on a straight line:
m = $\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}$
As a result, using the formula above, we can quickly determine the slope of a line connecting two locations. How much the line rises (along the y-axis) from one point to the other over the run (along the x-axis) is another way to describe the slope of a line between two locations.
The change in y is the fraction’s numerator, whereas the change in x is the fraction’s denominator. These are the slope situations and what they indicate for the rise and run
- Rise and run have the same sign when the slope is positive (both are positive or both are negative).
- Rise and run have opposite signs whether the slope is negative (one is positive, the other is negative).
- In the case of a slope of zero, rise and run can both be zero.
- Run and rise are both 0 when the slope is indefinite (infinite).
Some Examples of Run
Example 1
a) Using the rise-over-run method, determine the slope of the line connecting points X(0, 2) and Y(1, 3).
b) Using the rise-over-run method, determine the slope of the line connecting points X(0, 8) and B(2, 4).
c) Using the rise-over-run method, determine the slope of the line connecting points X(0, 7) and B(5, 3).
Solution
a) As we know, the equation of a straight line:
Y= mx + b
Using the slope formula:
Slope (m) = $\dfrac{y_{2}-y_{1}}{ x_{2}-x_{1}}$
m = $\dfrac{3-2}{1-0}$
m = 1
Point X passes through the line, so substituting the value of x, which is equal to zero, and y, which is two, in the equation of the line to evaluate b:
2 = 1(0) – b
b = -2
so substituting all the values in the equation of the line, we have:
y = x – 2
b) Equation of line:
Y= mx + b
Using the slope formula:
m = $\dfrac{4-8}{2-0}$
m = -2
Point X passes through the line, so substituting the value of x, which is equal to zero, and y, which is two in the equation of the line to evaluate b:
8 = -2(0) – b
b = -8
so substituting all the values in the equation of the line, we have:
y = -2x – 8
c) Equation of line:
Y= mx + b
Using the slope formula:
m = $\dfrac{3-7}{5-0}$
m = – 0.8
Point X passes through the line, so substituting the value of x, which is equal to zero, and y, which is two, into the equation of the line to evaluate b:
7 = -2(0) – b
b = -7
so substituting all the values in the equation of line, we have:
y = -0.8x – 7
Example 2
When Ali looked at the graph, she saw that the lift had been 30 units and the run had been 6 units. What value should a line’s slope have?
Solution
As given, the rise is 30 units, and the run is 6 units, and we know the formula for slope is:
Slope = Rise / Run
Slope = 30/6
Slope = 5
All images were created using GeoGebra.
