Scale|Definition & Meaning

What Is a Scale? 

Scale is the factor that gives the ratio between the length of the actual figure and drawing its portrait. Scale gives the measurement of how much the portrait or model is in resemblance to the real thing. Scale is much used in sketching and drawing. It may be expressed in ratios, words, and fractions.

Ever wondered how maps of huge-sized buildings and sculptures are constructed with precise measurements and everything accurately designed? Scaling helps in the cause of mapping such huge measurements to a small piece of paper, so it becomes easy to understand and convey to others.

In mathematics, scaling is a method in which an actual size object is narrowed down or scaled up in exact proportions so that it can be to be drawn on a piece of paper or whiteboard. In geometry, scaling refers to more or less extending or shortening structures in order to preserve their fundamental form. Identical figures are those which have been scaled.

Figure 1 – The larger rectangle has been scaled down to a smaller form

In the above figure, both shapes are similar to each other, but one rectangle is downsized, whereas the other one is in its actual shape. So to narrow down or shrink any large scaled sculpture, we take the use of a scale.

How To Scale Using a Scale Factor?

A scale is generally used to represent two models or images using a common relationship or by representing them in a ratio of their interconnected dimensions. Usually, the dimensions of the actual image are factored into another measuring scale. This measuring scale contains a common number known as the scale factor.

The scale factor is responsible for enlarging or shrinking an image. It is multiplied by all the components of the actual model resulting in a scaled image. A measuring scale and the scale factor are most commonly used in blueprints that are helpful in mapping construction sites.

Let’s suppose we need to construct an image of an eighty feet tall tree on a piece of paper. For this miracle to happen, we need to define an appropriate scale that fits our paper and accurately define our measurements.

We say that 10 feet are equal to a 1-inch scale which can be represented as 1:10, and in mathematical terms, it means that 1 unit in drawing perspectives will represent 10 units in the actual perspective.

So a tree that tall can easily fit in our paper when we scale it down to only 8 inches. So in the real world, the tree is 80 feet tall, but it can be represented as 8 inches on a piece of paper, thus indicating that a scale of 1:10 has been applied here.

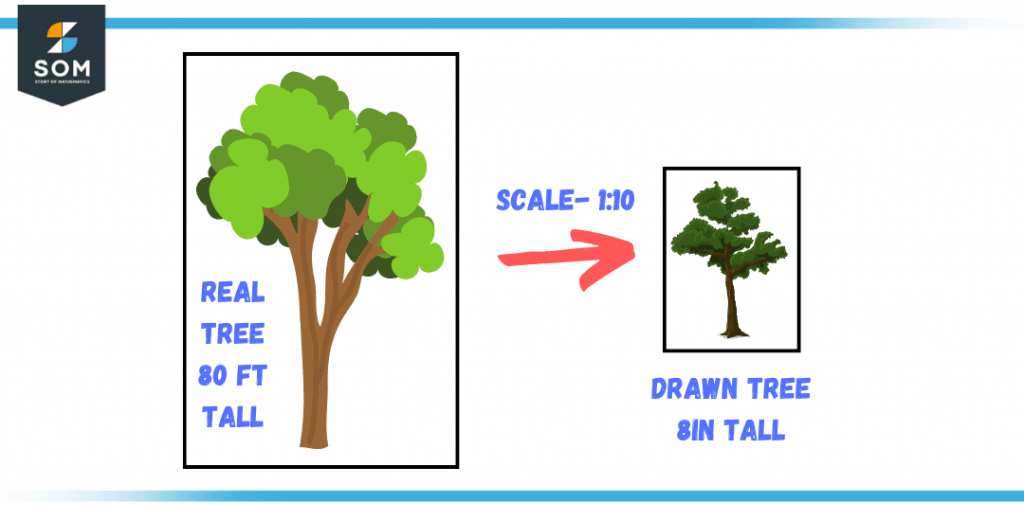
Figure 2 – 80ft tall tree has been scaled down to an 8in form

If there is not much information about the scale factor in a given set of images, then by knowing the actual dimensions of the original model and the drawn image, we can easily calculate the scale factor.

The formula to find the scale and the scale factor is as follows:

Measuring Scale = Measurements of scaled image : Measurements of the actual image

Scale factor = Measurements of scaled image / Measurements of the actual image

To better understand the formulas, let’s say a lamp pole is to be made that is 100 inches high in the absolute world but is portrayed as only 10 inches in the drawing. So the scale can be determined as 10:100 or 1:10, and the scale factor will be 1/10.

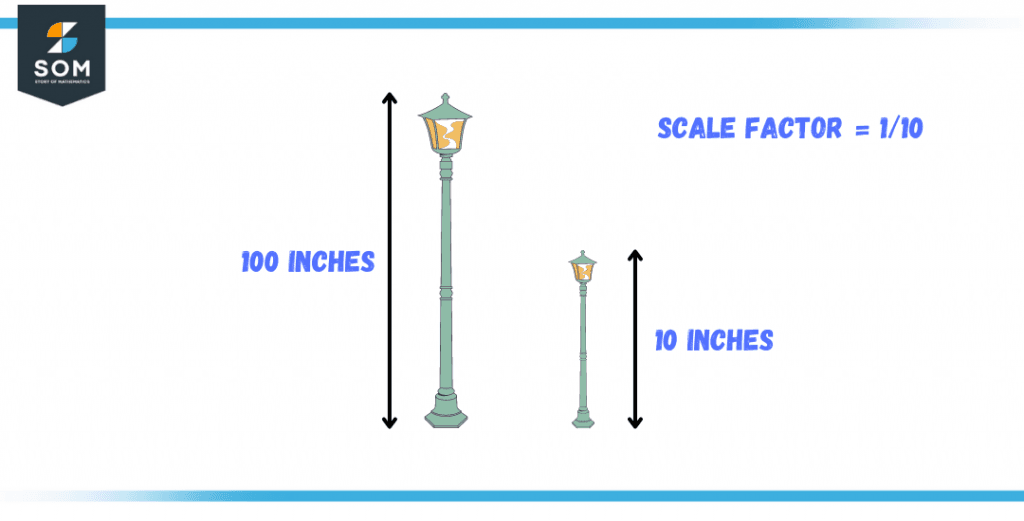
Figure 3 – A large pole has been scaled down to a smaller image

Scaling Types

Up-Scaling

Up-scaling means to enlarge something. When we want to view something in enlarged form, we scale up the smaller figure. In simple words, when the size of an image is increased as compared to its actual size, it indicates that the image has been scaled up. The formulas for scale and scale-up factor are constructed as:

Measuring Scale = Measurements of scaled image : Measurements of the actual image

Up-Scale factor = Enlarged image dimensions / Dimensions of the small image

In situations where the image is really compact, we may want to scale it up. To analyze a mosquito’s wings, for instance, we must sketch them out on canvas.

We would want to ramp up the mosquito because of its tiny dimension, as illustrated here.

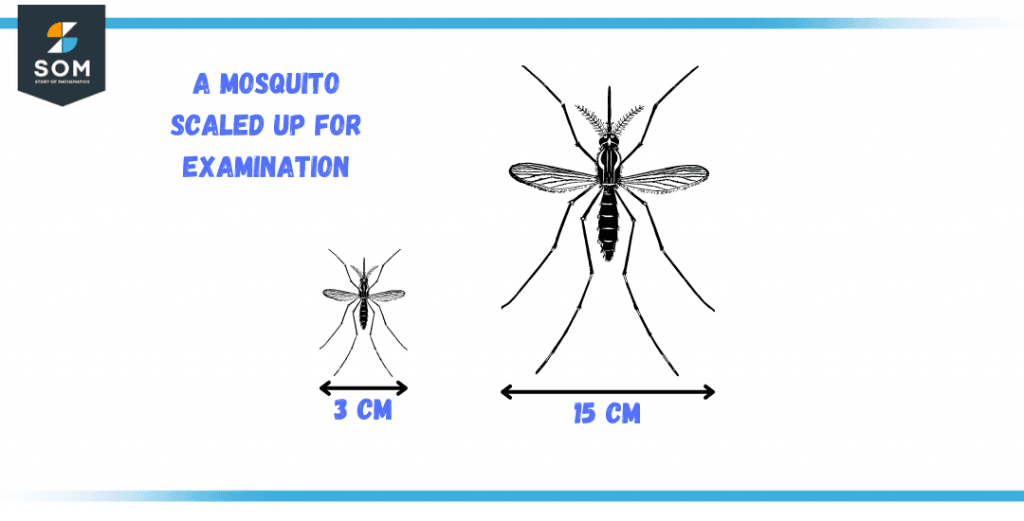
Figure 4 – A tiny mosquito enlarged by using the scale-up technique

Here, the scale factor is:

$\dfrac{15}{3}$ = 5 > 1

As you can see, the scale factor for enlarging an image will always be bigger than 1. Let’s say we have another scenario where one image is 4 times larger than the smaller image, so we get the scale factor as 4 since the ratio is 1:4, thus making it greater than 1. The smaller models are referred to as preimages, whereas the enlarged model is known as an image.

Down-Scaling

Down-scaling means reducing the size of something. When we want to view a big figure in a smaller form, we scale down the large figure. In simple words, when the size of an image is decreased as compared to its actual size, it indicates that the image has been scaled down. The formulas for scale and scale down factor are formed as:

Scale = Measurements of scaled image : Measurements of the actual image

Down-Scale factor = Reduced image dimensions / Dimensions of the Larger Image

In situations where the object is really big, we may want to scale it down. To construct a master bedroom, for instance, we must sketch it out on paper.

Let’s say the actual size of the bedroom is 240 inches by 210 inches. Since it’s rather a difficult task to draw it on paper, we must scale it down to a drawable size, such as 8 inches by 7 inches.

Here, the scale factor is:

$\dfrac{8}{240}$ = $\dfrac{1}{30}$ < 1

As you can see, the scale factor for shrinking an image will always be smaller than 1.

Let’s say we have another scenario where one image is 4 times smaller than the larger image, so we get the scale factor as 1/4 since the ratio is 4:1, thus making it smaller than 1. The smaller models are referred to as images, whereas the actual model is known as a preimage.

Solved Examples Related To Scale

Example 1

Determine the length of an actual sculpture if the length of the scaled figure is 5 units and the scale ratio is 1:25.

Solution

\[ \dfrac{\text{Scaled Height}}{\text{Actual Height}} = \dfrac{1}{25}\]

\[ \dfrac{5}{\text{Actual Height}} = \dfrac{1}{25}\]

Actual Height  = 5 $\times$ 25 = 125 length units

Example 2

A triangle now has new dimensions of 6 cm by 10 cm by 12 cm after being scaled up by a scale factor of 2. What will be the original dimensions of the triangle?

Solution

Given new dimensions, 6 cm, 10 cm, and 12 cm, and the scale factor of 2, the formula for the scale factor is:

Scale factor = $ \dfrac{\text{Measurements of scaled image}}{\text{Measurements of the actual image}} $

Substituting the values for all three sides gives:

• 2 = $\dfrac{6}{\text{Actual Dimensions}}$

Actual Dimensions = $\dfrac{6}{2}$ = 3 cm

• 2 = $\dfrac{10}{\text{Actual Dimensions}}$

Actual Dimensions = $\dfrac{10}{2}$ = 5 cm

• 2 = $\dfrac{12}{\text{Actual Dimensions}}$

Actual Dimensions = $\dfrac{12}{2}$ = 6 cm

Hence the original dimensions of the triangle are 3 cm, 5cm, and 6 cm.

All images are created using GeoGebra.

Sample Point Definition < Glossary Index > Scalene Triangle Definition