Scientific Notation|Definition & Meaning

What Is Scientific Notation? 

A number can be expressed using scientific notation if it is too large or tiny to be conveniently represented in decimal form. This occurs when the number has an excessively long sequence of digits if expressed in decimal form.

Figure 1: Representation of scientific notation.

There are a few other names for this form, including scientific form, standard index form, and written form in the UK. Because it makes some arithmetic operations easier to perform, this notation with a base of 10 is frequently used by science, mathematics, and engineering professionals. This display style is typically called the “SCI” mode on scientific calculators.

In scientific notation, nonzero values are represented in the form m n, which can also be expressed as m multiplied by ten and then raised to the power of n. In this form, n is an integer, and the component m is a nonzero numerical value. The natural number m is referred to as the significand or mantissa, whereas the integer n is referred to as the exponent.

Because “mantissa” is also the conventional name for the fractional component of the common logarithm, using the term “mantissa” concerning logarithms might lead to confusion since it has two distinct meanings. In conventional decimal notation, a minus sign comes before the m symbol if the expressed value is less than zero.

Scientific notation and the computer arithmetic method known as decimal floating point are closely related.

How Is the Notation Used in Standard Form?

If the exponent of 10 is negative, the decimal point (if there is one) should be moved to the left when converting a figure from scientific notation to standard form; if the exponent of 10 is positive, the decimal point should be moved to the right.

To ensure that the final representation does not contain any multiples of 10, we will need to move the decimal point the same number of times that the exponent implies in power.

Significant Figures

A figure in a number that contributes to the accuracy of the total is referred to as a significant figure. This contains all the numbers that are not zero, as well as any zeroes indicated to be significant, whether they are between significant digits or not.

Because their sole purpose is to illustrate the number’s magnitude, preceding and following zeroes are not considered significant digits. This, however, contributes to ambiguity in the situation. The number 5607800 is typically read as having five significant figures, 5, 6, 0, 7, and 8, with the latter two zeroes serving as placeholders and contributing no more precision to the reading.

However, if the final two digits were likewise measured precisely and it was discovered that they equaled zero, then the same number would be utilized in seven significant figures.

When a number is transformed into normalized scientific notation, it is reduced to a value between 1 and 10 on a scale of 1 to 100. There is no change to any significant digits. However, the zeroes serving as placeholders are no longer necessary.

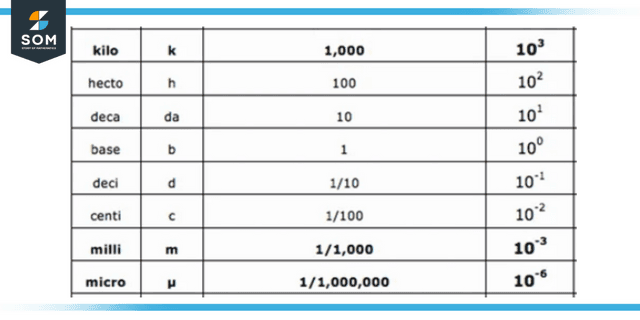
Figure 2: Table of scientific notation.

Estimated Final Digits

In the practice of scientific measurement, it is common practice to write down all of the definite digits that are known to have resulted from the measurement and to make an educated guess for at least one increased digit if there is any knowledge at all available on the value of the variable in question.

The final number contains more information than it would if it were missing the extra digit, which may be regarded as a significant digit because it communicates some information and contributes to improved precision in measurements and the agglomerations of observations (adding them or multiplying them together)

The Rules of Scientific Notation

We must follow the rule mentioned below to calculate the power or exponent of 10.

• Ten should always serve as the base to braised to some power in decimal number systems.
• The exponent needs to be a number greater than zero, meaning it can take either a positive or a negative value.
• The coefficient has a value in absolute terms that is either more than or equal to 1, but it should be under 10.
• Positive or negative numbers and whole and decimal numbers can be used to represent coefficients.
• The remainder of the significant digits of the value is contained within the mantissa.

With the help of the following representation, let us determine how many places the decimal point needs to be moved after the single-digit number:

• If the number is greater than 1, then the decimal point must be moved to the left, and the power of ten will be positive. If the given number is less than 1 (but greater than 0), then the power of 10 will be negative.
• For example, in scientific notation, 6000 is written as 6 x 10³. On the other hand, 0.0006 is written as 6 x 10^-4.

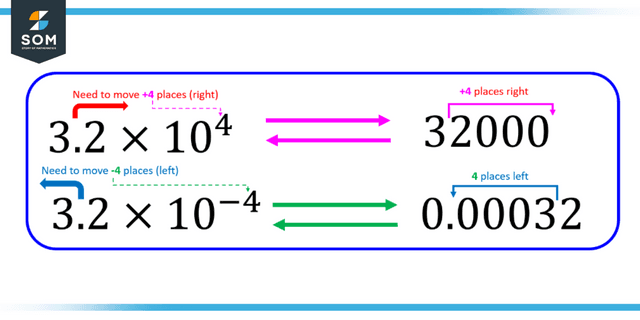
Figure 3: Representation of positive and negative scientific notation.

Rules Comprising the Scientific Notation System

The following is a rundown of the five rules that govern scientific notation:

• The starting point should always be 10.
• The exponent needs to be a number greater than zero, meaning it can take either a positive or a negative value.
• The coefficient has an absolute value that is more than or equal to 1, but it should be less than 10.
• Coefficients can take the form of numbers that are either positive or negative, including whole integers and decimal amounts.
• The remainder of the significant digits of the number is contained within the mantissa.

Examples of Scientific Notation

Example 1

Change the given number into scientific notation: 4392.5.

Solution

The scientific notation of the above number is 4.392 x 10³.

Example 2

Change the number 0.00093 into scientific form if the decimal point is followed by a non-zero digit.

Solution

The above number can be written as: 9.3 x 10^-4.

All images/graphs are created using GeoGebra.

Scalene Triangle Definition < Glossary Index > Sector Definition