Sector|Definition & Meaning

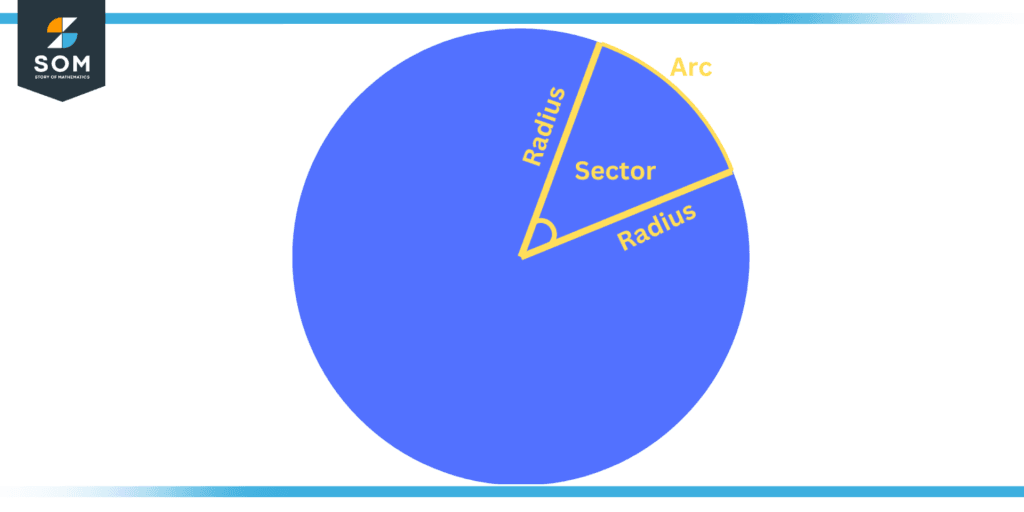
Figure 1: Illustration of a Sector

Area of a Sector

The total space that is contained within the perimeter of a sector of a circle is referred to as the area of that sector of that circle. Every beginning point for a sector is located at the circle’s epicenter. The Semi-circle of any circle can also be considered a sector. In that scenario, however, a circle will be said to have two sectors where both sectors will possess the same amount of area.

Now let us get familiar with the formula for determining the total area of a sector. Let us assume that ‘r’ is the radius of the circle whose sector’s area we want to determine. Let us also assume that ‘θ’ is the angle of the sector whose are we want to find. Then the formula below can be employed to find the area of the sector:

Area of Sector = A = (θ/360°) × πr²

Here, ‘θ’ refers to the angle of the sector in degrees, and ‘r’ refers to the radius of the circle.

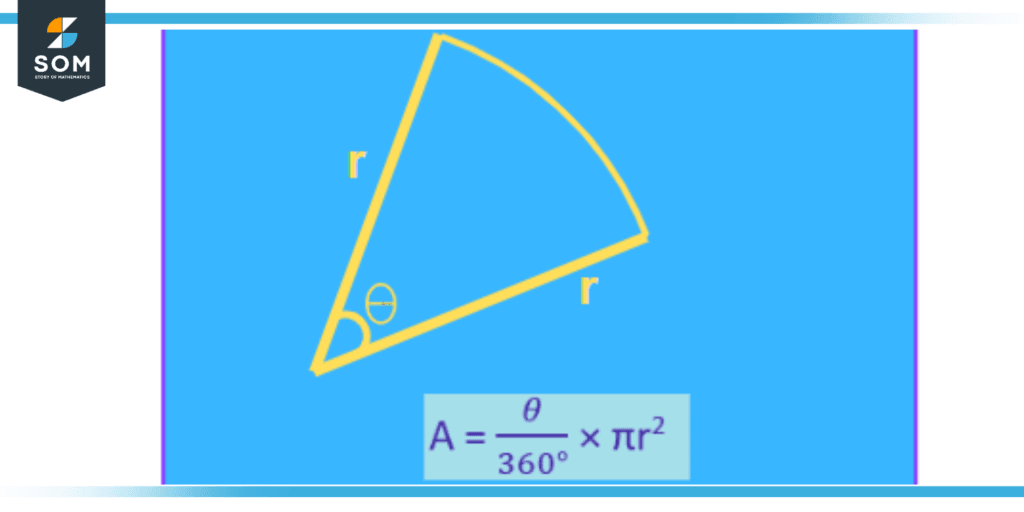
Figure 2: Illustration of Area of Sector

The Area of the Sector in Relation to the Length of the Arc

There is an additional method for determining the area of a sector that can be utilized in the event that the length of the arc of the sector rather than the angle of the sector is provided. Let’s say that the length of the arc is denoted by the letter ‘L.’ If the radius of a circle equals r units, then an arc that is exactly r units in length will form exactly one radian at the circle’s center.

Therefore, one can draw the conclusion that an arc with a length ‘L’ will subtend an angle with a measure of r/L, which is the angle at the center. Therefore, if ‘L’ represents the length of the arc, r represents the radius of the circle, and θ represents the angle that is formed at the center, then:

θ = L/r

‘θ’ here refers to the angle in radians.

Now let us incorporate the value of θ in the area of the sector:

Area of Sector = A = (θ) × πr²

A = (L/r) × (r²/2)

A = (L × r)/2

Perimeter Formula for a Sector

As we know that perimeter refers to the summation of the length of boundaries of any geometrical shape. Using the same concept, we can derive the formula for the perimeter of a Sector of any circle. Below we have done the derivation for the formula of the perimeter of a sector.

If we assume that ‘r’ is the radius of the circle, ‘θ’ is the angle subtended by the sector on the circle center, and ‘L’ is the length of the arc, then:

The perimeter of a sector = 2r + arc length

Since we know that:

Arc length of a sector = L = (θ/360) × 2πr

Thus:

The perimeter of a sector = 2r + ((θ/360) × 2πr )

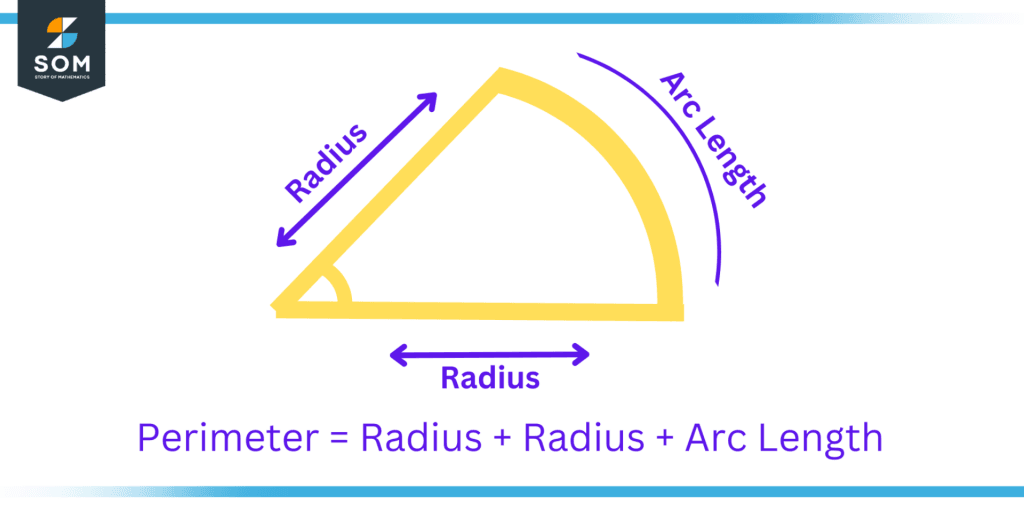
Figure 3: Illustration of Perimeter of Sector

Sector Proportion

The area of one sector of a circle in relation to the total area of the circle is what is meant by the term “sector proportion.” It is denoted by the symbol pi (from the Greek alphabet), and its value is about 3.14159. The formula for calculating the proportion of a sector is as follows:

(Area of the sector of a circle) / (Area of the complete circle) = (θ/360) × π

Here ‘θ’ refers to the value of the central angle in degrees.

For instance, if a sector has a central angle of 45 degrees, the sector proportion can be calculated as:

Sector proportion = (45/360) × π

Sector proportion = 0.125 π

This indicates that the area of the sector constitutes 12.5 percent of the total area of the circle.

The notion of sector proportion is essential in maths as well as in other domains since it enables a contrast of the area of a sector to the area of the complete circle. This analysis can be helpful in real applications such as computing the percentages of a pie chart, as well as when dealing with calculations of angles and circular parameters.

Applications of Sectors

The use of sectors of circles can be found in a diverse array of contexts and fields. The following are some of the more typical applications:

Engineering

Sectors are utilized in the field of engineering to describe and analyze a wide variety of data, including pulley systems and gear teeth, amongst other things. Calculating the strength and tension of circular constructions such as pipes and discs is another application for these equations.

Physics

In the field of physics, sectors are a useful tool for representing and analyzing a wide variety of phenomena, including angular momentum and centripetal force, amongst others. They are also employed to compute the area of a sector as well as the arc length, which is something that can be helpful when trying to solve problems relating to physics.

Mathematics

Sectors are a useful tool for representing and analyzing a wide variety of geometric figures and forms in the field of mathematics. Calculating the size and arc length of a sector, which may be helpful when attempting to solve geometric issues, requires the use of these tools.

Graphing and Data Visualization

Sectors are frequently used to depict the proportion of various data sets when pie charts, as well as related types of data visualization, are utilized.

Navigation

In navigation, sectors are used to both depict the various parts of maps and to assist navigators in locating themselves in relation to the map.

Biology

In the field of biology, separate parts of organisms, such as individual sections of leaves or the petals of a flower, are referred to as “sectors,” and they are represented by the term.

Examples of Sectors

Example 1

Calculate the arc length of a sector if the angle of the sector is 60 degrees and the radius of the circle is 6 meters.

Solution

Since we know that:

Arc length of a sector = L = (θ/360) × 2πr

According to the given data:

θ = 60⁰

r = 6 m

Now:

Arc length of a sector = L = (60/360) × 2 × π × 6

L = 2 × π

L = 44/7 m

Example 2

Calculate the area of a sector of a circle whose radius is 3 m and the length of the sector’s arc is 10 m.

Solution

Since we know that:

A = (L × r)/2

According to the given data:

L = 10 m

r = 3 m

Now:

A = (10 × 3)/2

A = 15 m²

All images/mathematical drawings were created with GeoGebra.