JUMP TO TOPIC
Semi|Definition & Meaning
Definition
Semi literally means “half.” It is used as a prefix to imply halves of various things. For example, semi-annually means every half-year (e.g., interest compounding), semicircle means a half circle, and semi-major and minor axes mean half the major and minor axes of ellipses. It is also used in other contexts, as in semiprime numbers (a product of two prime numbers).
A prefix that means “half” is known as a semi. The most common example of the semi is a semi-circle and semiannually. Let’s first explain the semi-circle in detail. The following figure represents the semi-circle.
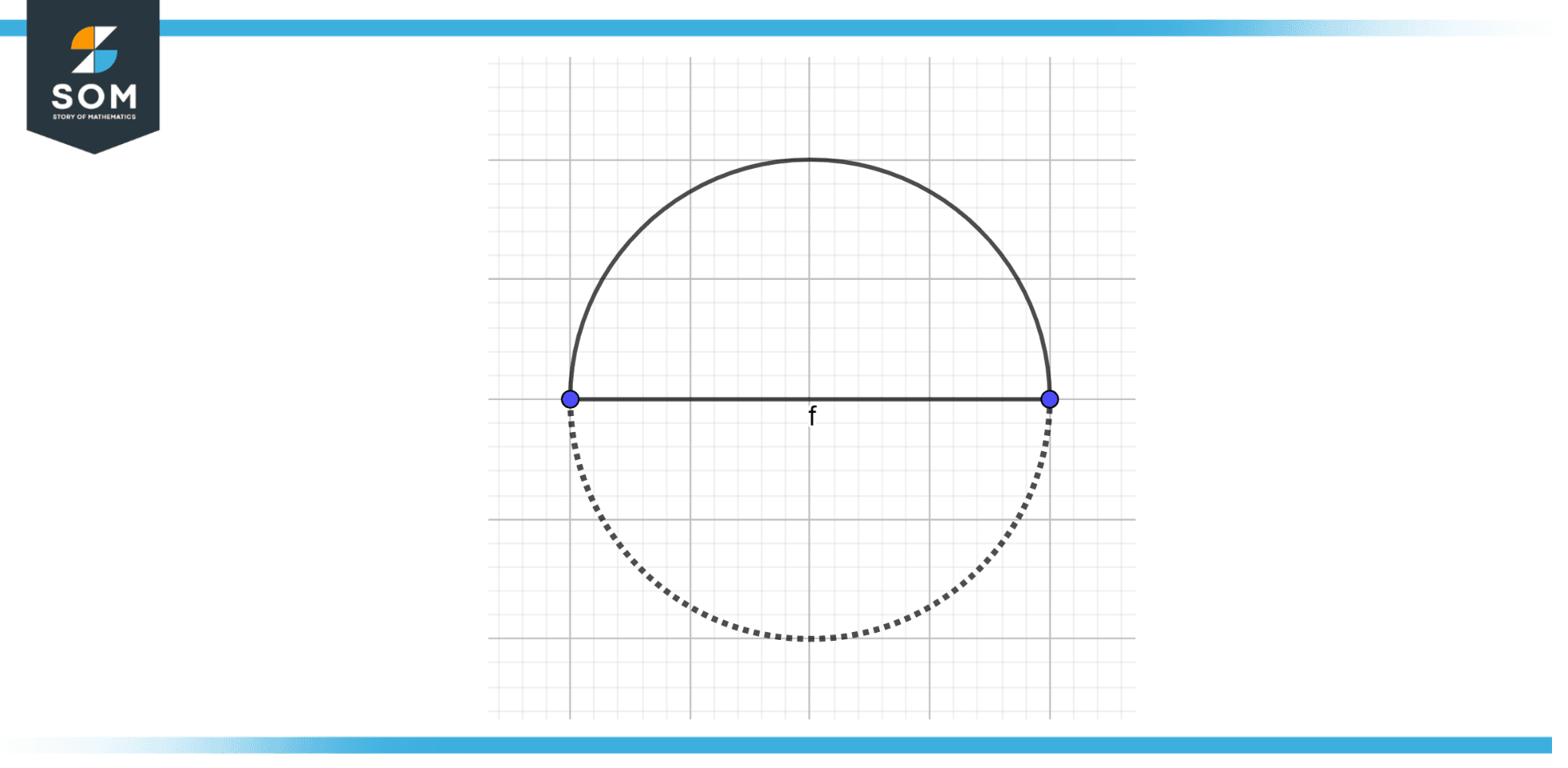
Figure 1 – Representation of semi-circle
The figure below represents the semi-polygon.
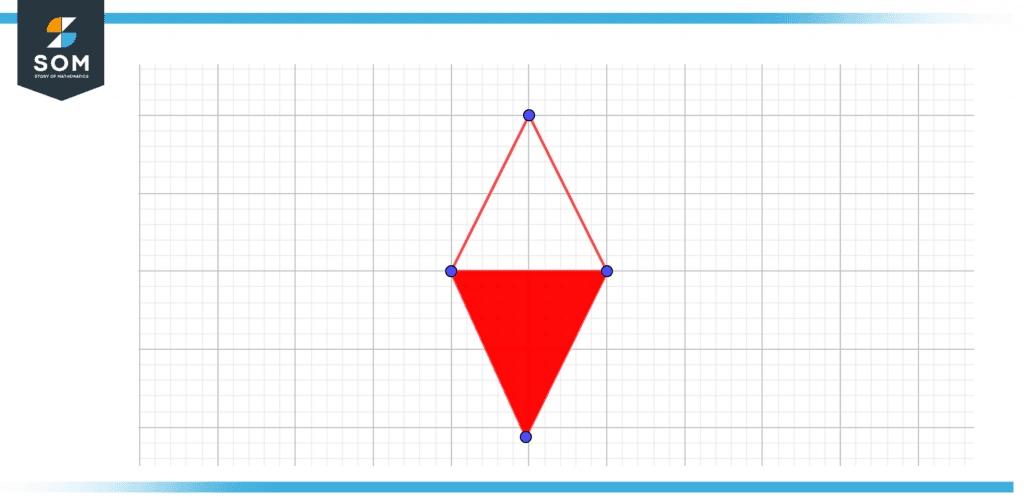
Figure 2 – Semi-polygon representation
What Is a Semi-circle?
A semicircle is a half-circle created by splitting a circle into two equal parts. It is created when a line pierces the circle’s center and touches its two ends. The circle’s diameter is the name given to this line.
Taking a whole circle and slicing it in half along its diameter yields a semicircle, which can also be referred to as a half-circle. Only one line of symmetry, known as the reflection symmetry, may be found in the shape of a semicircle. A half-disk is another name for a shape that resembles a semicircle.
Since a semicircle is only half of a circle, its arc will always measure 180 degrees because 360 degrees is the total number of degrees in a circle.
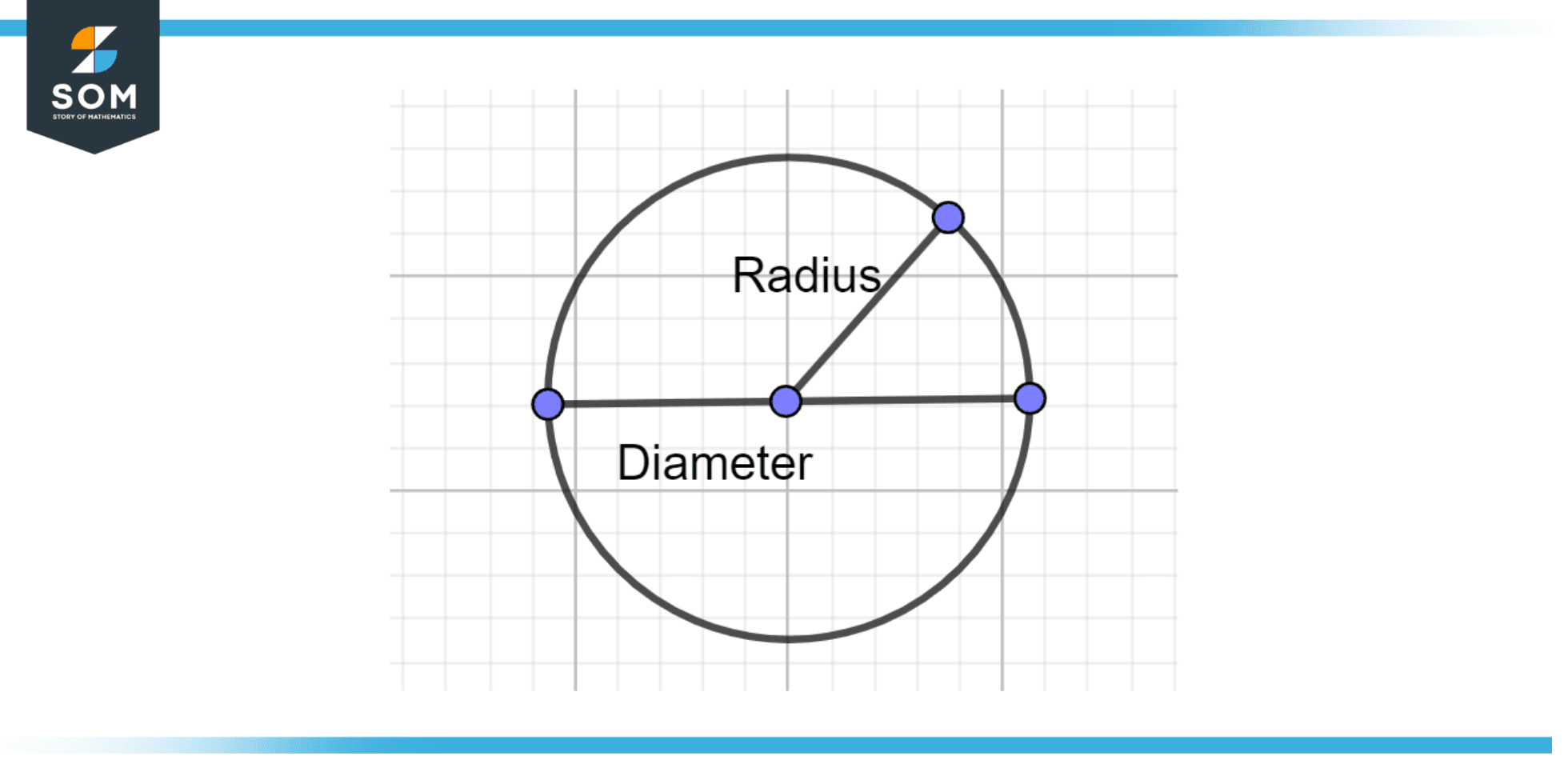
Figure 3 – Circle representation
Finding a Semicircle’s Area
The interior or the surrounding area of such a semicircle is referred to as its area. It has a circle’s half surface area. Remember that a circle’s area is equal to πr², where the circle’s radius is denoted by r and pi (π) is approximately equal to 22/7 = 3.14. Thus, the following equation can be used to determine a semicircle’s area:
Area of semi-circle is = ½ × πr²
Finding a Semicircle’s Circumference and Perimeter
The perimeter or circumference indicates the length of the semicircle’s entire boundary. Contrary to popular belief, a semicircle’s perimeter is not equal to half that of a circle because a circle’s half-perimeter only yields the curved portion’s perimeter. The bottom diameter line must be added to the bottom circumference to get the whole perimeter.
Remember that a circle’s radius is 2πr. Therefore, the circumference of the semicircle’s curved portion is equal to 1/2 of 2πr equal to πr. Let’s now provide the diameter’s length as well, so the semicircle’s total perimeter is equal to πr + d, where d is its diameter.
However, we are also aware that a circle’s diameter is equal to twice its radius. As a result, we find that the semicircle perimeter is equal to πr + 2r. We can take r common, so the perimeter = r (π + 2).
Characteristics of a Half Circle
The following is a list of some essential characteristics of a semicircle, which together make it a distinctive form in geometry:
- A closed two-dimensional shape is known as a semicircle.
- Due to the fact that one of its edges is bent, it cannot be considered a polygon.
- One of the edges of a semicircle is curved, and this edge is known as the circumference. The other edge is straight, and this edge is known as the diameter.
- It corresponds to precisely one-half of a circle. Both semicircles that were generated out of the circle had the same diameter as the circle itself.
- A semicircle has an area equal to one-half that of a full circle.
What Is a Semi-Annual?
The word “semiannual” designates events that occur twice a year, often once every six months, and are paid for, reported, published, or take place in another manner.
For instance, the interest on a general obligation bond with a term of ten years that was issued in 2020 by Buckeye City, Ohio Consolidated School District will be paid on a semiannual basis each year up to the maturity date of the bond in 2030.
When an investor purchases these bonds, he or she will be entitled to interest payments twice during each of those years, specifically, once in the month of June and once in the month of December. The school system will also issue a semiannual financial report in February and November.
A Detailed Explanation of Semi-Annual
The term “semiannual” refers to something that takes place twice yearly and is merely a word. For instance, a business may hold workplace parties on a semiannual basis, a couple could celebrate their marriage anniversary on a semiannual basis, and a family could take a vacation on a semiannual basis. The term “semiannual” refers to occurrences that take place twice yearly.
If a company decides to pay its shareholders a dividend on a semiannual basis, then those shareholders will be entitled to dividend payments on two separate occasions each year. A corporation has the ability to decide whether or not to deliver dividends on an annual basis. Quarterly (or four times a year) publications of financial statements or perhaps even reports are common practice.
It is quite unusual for companies just to publish their financial results every other year. However, they do provide an annual report, which, according to the dictionary definition, must be done at least once every year.
When purchasing bonds, it is essential to have a solid understanding of the semiannual payment schedule. The yield that a bond pays its holder is typically used as a way to characterize the bond. A bond with a face value of $2,000 might have a yield of 5%, for instance.
To have a better understanding of the payment that you would get as the bondholder, it’s indeed essential to understand if this 5% has been paid annually or semiannually.
A Numerical Example of a Semi-circle
Example 1
A semicircle has a diameter of 7 cm. Determine the curved surface’s perimeter.
Solution
Given that:
The circle has a 7 cm diameter.
Radius = 7/2 cm.
Semicircle’s curved surface’s perimeter is equal to 1/2 * 2πr.
= ½ × 2 × 22/7 × 7/2
= 11 cm
Example 2
A semicircle has a diameter of 8 cm. Determine the curved surface’s perimeter.
Solution
Given that:
The circle has a 7 cm diameter.
Radius = 8/2 cm.
Semicircle’s curved surface’s perimeter is equal to 1/2 * 2πr.
= ½ × 2 × 22/7 × 8/2
= 12.56 cm
All mathematical drawings and images were created with GeoGebra.
