JUMP TO TOPIC
Semicircle|Definition & Meaning
Definition
A semicircle is one-half of a circle. Any circle can be split into two semicircles by cutting it with a straight line passing through the center and touching the circle at the two far ends. This line is called the circle’s diameter. The area of a semicircle is exactly half the area of the circle ($\pi$r$^2$/2), and its perimeter equals half the circumference plus the diameter ($\pi$r + d).
Figure 1 below shows a semicircle.
Figure 1 – Representation of a circle.
A semicircle is made by dividing a circle in half across its diameter. The two pieces are the same size. A semicircle, a half-disk, is a folded circular paper sheet in half. The semicircle has one symmetry line, which is called the reflection symmetric. The semicircle’s arc constantly measures 180° since it is half the 360° circle.
The semicircle is probably included among all commonly encountered geometric forms in the form of even a protractor. A semicircle comprises half of a circle, but real-world examples include a railroad trench, an igloo, half a melon, and many more. When drawn on a 2D plane, these forms resemble a semicircle.
A semicircle is described in geometry as a half circle generated by dividing a circle in half. It is produced by a line major axis and contacting both of the circular’s ends. This line represents the circle’s diameter.
Figure 2 below shows the diameter and radius of a semicircle.
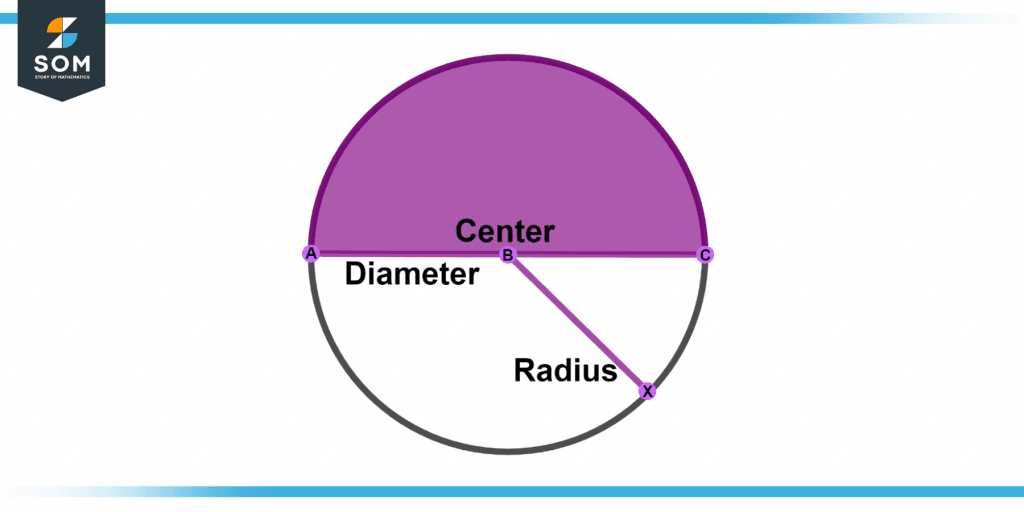
Figure 2 – Diameter and radius of a semicircle.
Semi-circles are formed whenever an arc of the circle, including its ends on the diameter, divides a circle into two identical halves. It is the most prevalent shape in everyday life, such as the protractor, tachometer, taco, etc.
Semicircle Properties
A few essential aspects of the semicircle that can make it a distinctive form in geometry are listed below:
- A semicircle is a complete two-dimensional shape.
- Because it has a bent edge, it isn’t a polygon.
- A semicircle contains a single curved edge called the circumference and one straight edge called the diameter.
- It forms precisely half of a circle. The diameters of the circular and its two semicircles are the same.
- A semicircle’s area is half that of a circle’s area.
Semicircular Area
A circle’s region or interior space is referred to as its area. Given that a semicircle equals half a circle, then an area of a semicircle will be half that of a circle. The area of the semicircle refers to a space contained within it or the region around it. It has half the surface area of the circle. The area of the circle is thus $2\pi r^{2}$, where the radius r of a circle. Hence,
Semicircle area = $\frac{\pi r^{2}}{2}$ sq units
where R seems to be the radius of a semicircle
$\pi$ is roughly $\frac{22}{7}$ or 3.142.
Circumference of a Semicircle
The semicircle’s diameter is half the circumference of said circle. The circumference of a semicircle is described as the length of the arc that forms it. It does not include the diameter’s length.
The expression again for a circle’s circumference, as we know, is $2 \pi r$, where r is the radius. As a consequence, the semicircle’s circumference equals $\frac{2\pi r}{2} = {\pi r}$
Semicircle Perimeter
A semicircle’s perimeter is the sum of its circumference and diameter. It is not comparable to the area of a semicircle, i.e., its perimeter is not half the circumference of a circle. To determine the perimeter of the semicircle, we must first know the radius or diameter of a circle, as well as the length of an arc.
The circumference of the semicircle is required to calculate the length of an arc. Since the circumference equals C = $pi r$, where C seems to be the circumference and R is indeed the radius, we may calculate the perimeter of the semicircle as follows:
Semicircle perimeter = ($\pi$R + 2R) units, perhaps after calculating the R,
semicircle perimeter = R($\pi$ + 2) units
The angle created either by line segments traced from each end of a diameter toward any point just on a semicircle is known as the inscribed angle. The angle written is always 90°, no matter where another line intersects the semicircle. The angle B in the figure below is 90 degrees, while the diameter length AC is 180 degrees.
Because the semicircle equals half of the circle, the angle generated by an arc that transforms the circle into a semicircle is 180°.
Inscribed Angle in a Semicircle
The angle created either by line segments traced from each end of a diameter toward any point just on a semicircle is known as the inscribed angle.
The angle written is always 90°, no matter where another line intersects the semicircle. The angle B in the figure below is 90 degrees, while the diameter length AC is 180 degrees. Because the semicircle equals half of the circle, the angle generated by the arc that transforms the circle into a semicircle is 180°.
Figure 3 below shows the Inscribed Angle in a Semicircle.
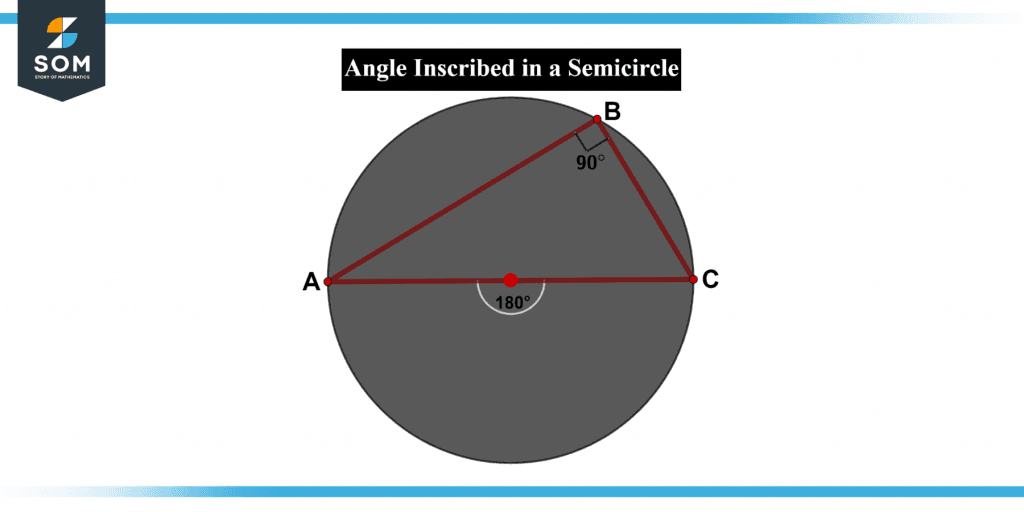
Figure 3 – The inscribed angle of a semicircle.
Examples of Semicircle
Some examples of semicircles are given below
Example 1
A lawn in the form of a ring with a circumference of 12 yards is located next to Dan’s residence. What’s the perimeter of an area of the garden that Dan wishes to utilize for a party?
Solution
Given that the diameter is 14 yards, we must calculate the radius.
Radius = Diameter multiplied by 2 = 14 multiplied by 2 = 7 yards
Therefore, the perimeter of the semicircle = R($\pi$ + 2), where $\pi$ is approximately 3.142.
Circumference Equals 7 (3.142 + 2)
Perimeter = 7.142
The perimeter is 35.994 yards.
As a result, the circumference of half the garden Dan will utilize is 35.994 yards.
Example 2
A radius of a round cake equals eight units. Calculate the area for half the cake.
Solution
We understand that the radius is equal to 8 units. A semicircle’s area Equals $\frac{\pi r^{2}}{2}$ square units.
Area equals (22 × 8)/2
88 square units of area
As a result, half of a cake has an area of 88 square units.
All Images are made using GeoGebra.
