JUMP TO TOPIC
Semiprime|Definition & Meaning
Definition
A semiprime number is the product of precisely two prime numbers, where the two prime numbers may be the same or different. Therefore, 5 x 5 = 25 and 17 x 7 = 119 are semiprime numbers since 5, 17, and 7 are all prime numbers. All semiprime numbers are composite numbers.
What Is a Semiprime?
A composite number combining two (potentially equal) primes is called a semiprime. This number type is referred to as a 2-almost prime, prime, or PQ-number.
The initial handful is composed of 4, 6, 9, 10, 14, 15, 21, 22, and so on. The first few semiprimes whose factors are different (also known as square-free semiprimes) are the numbers 6, 10, 14, 15, 21, 22, 26, 33, 34, and so on.

Figure 1: Representation of semiprime numbers from 1-100
The definition of a semiprime is that it must be the square of a prime number. Therefore, the square of the largest recorded prime is the largest known semiprime that is known to exist.
The following are some examples of semiprime numbers with a value less than 10n: 3, 34, 299, 2625, 23378, 210035, etc.
For the equation n=pq in which p and q are both distinct, the congruence pq=p must be met (mod n).
Furthermore, the totient function conforms to the elementary identity phi(n)=(p-1), which can be expressed as follows: (q-1).
It is a complex task to produce verifiable semiprimes with more than 250 digits by employing strategies other than multiplying two primes together. The process of factorization is one option. According to the Cunningham project, the factored semiprimes (6(353)-1)/5 and 2(997)-1 have a total of 274 and 301 digits, respectively.
In an analogous manner, the indexes of Mersenne numbers that produce semiprimes are the integers 4, 9, 11, 23, 37, 41, 49, 59, 67, 83,…. 1427 and 1487 are the most significant known indices that give rise to semiprimes as of the year 2022.

Figure 2: Representation of Mersenne prime
Don Rebel demonstrated in 2005 how an elliptical pseudo-curve and the Goldwasser-Kilian ECPP theorem might be used to construct a 1084-digit provable semiprime even in the absence of a known factorization of the number.
Subsequently, it established a backdoor strategy, factored Reble’s 1084-digit semiprime, and proposed a new way to issue a semiprime certificate that is at least as effective as random semiprimes of the same size. All of these accomplishments were accomplished in the same year.
Encryption methods like RSA rely on particular huge numbers that have as their factoring factors two huge primes.
Applications of Semiprime
Semiprimes have several applications in cryptography and numerical methods, but their most notable use is in public key cryptography.
This is because RSA and other pseudorandom number generators, such as Blum Blum Shub, rely on semiprimes to generate random numbers. These methods rely on the notion that it is computationally straightforward to locate two huge primes and multiply them combined (resulting in a semiprime). Yet, it is difficult to find the original components.
RSA Security held a competition known as the RSA Factoring Challenge and offered prizes for successfully factoring various large semiprimes. Several participants were successful and received awards. The first RSA Factoring Challenge was published in 1991, and the New RSA Factoring Challenge succeeded it in 2001. However, the New RSA Factoring Challenge was eventually discontinued in 2007.
In 1974, a radio signal directed toward a group of stars was used to transmit the Arecibo message.
Properties of Semiprime
The semiprime N=pq, where both p and q are prime numbers, is considered one of the more significant quantities in the study of number theory. This combination is essential to modern cryptography since it is difficult to factor when N is extensive but very easy to construct when the prime components are known. Because of this, it plays a crucial role in modern cryptography.
Let us show this is true using the semiprime number N=1373 x 3217, which equals 4416941. It is easy to get to the seven-digit long semiprime by multiplying the two primes together. However, it is far more challenging to determine what contributes to it. It is always possible to assume that p is more minor than sqrt(N)=2101.6519, which means that q will be higher than sqrt (N).
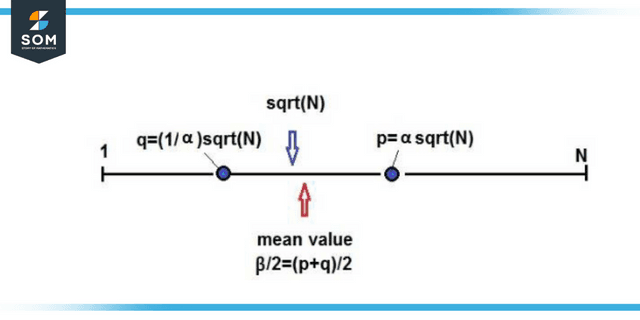
Figure 3: Properties of Semiprime number
Examples of Semiprime Numbers
Example 1
From the given numbers below which numbers are semi prime numbers.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 50.
Solution
2 * 2 = 4
2 * 3 = 6
3 * 3 = 9
2 * 5 = 10
2 * 7 = 14
3 * 5 = 15
3 * 7 = 21
2 * 11 = 22
5 * 5 = 25
2 * 13 = 26
3 * 11 = 33
2 * 17 = 34
5 * 7 = 35
2 * 19 = 38
3 * 13 = 39
2 * 23 = 46
7 * 7 = 49
These are the semiprime numbers that occur between 1 to 50.
Example 2
From the given numbers below which numbers are semi prime numbers.
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100.
Solution
3 * 17 = 51
5 * 11 = 55
3 * 19 = 57
2 * 29 = 58
3 * 21 = 62
5 * 13 = 65
3 * 23 = 69
2 * 37 = 74
7 * 11 = 77
2 * 41 = 82
5 * 17 = 85
2 * 43 = 86
3 * 29 = 87
7 * 13 = 91
3 * 31 = 93
2 * 47 = 94
5 * 19 = 95
These are the semiprime numbers that occur between 51 to 100.
All images/graphs are created using GeoGebra.
