JUMP TO TOPIC
Senary|Definition & Meaning
Definition
A senary (or heximal) number is one that is based on the Senary Number System, which has a base of 6 (i.e., uses only six digits from 0–5). Therefore, Decimal numbers from 0–5 are equal to the Senary numbers from 0–5, but a Decimal 6 equals a Senary 10. From Senary 10–15, the equivalent Decimals are 6–11. Then, the Decimal 12 equals a Senary 20, and so on.
What Is a Senary Number?
A senary number is a number having a base of six. It is also known as base-6 numbers or heximal numbers. The numeral system based on this number is known as the senary numeral system.
Usually, the number system used in most of our daily routines is the base-10 numeral system, in which digits from 0 to 9 are used as the basis. This system is not widely adopted by significant cultures but is rather famous in a number of independently small communities. Just like the decimal number system, it is a product of two prime numbers (2 x 3), so it can be referred to as a semiprime.

Figure 1 – Digits involved in the Senary numeral system
The very first approach to solve the 2 and 3 division problems is senary, or base-6. Senary offers several advantages compared to other systems we have previously thought about, but this is not the only one.
Another benefit of senary is that it’s considerably simpler to learn. Every one of its values falls within the range of a person’s intrinsic comprehension, which really is (5). As a result, its arithmetic formulas are quite simple and very easy to learn.
Counting to base 6 is more clean and easy. Base 10 can generally connect with our 10 binary fingers, while base 6 typically relates mutually with our hand as an abacus – a one-to-one image of position counts. To count in hexadecimal, represent the number 1 with one hand and the number 6 with the other. Anyone can efficiently count to 35 using this approach.
Whereas sometimes the senary system may not seem to be entirely perfect. As immaculate as it may sound, it still contains a couple of disadvantages on its own.
The first disadvantage to look into is the length of numerical values. It may be easy to count the first 35 senary numbers by hand, but they tend to be far bigger than their decimal companions. Although the senary numbers still require four fewer numerals to represent themselves, which holds them to have a slight advantage over other numeral systems.
The other disadvantage of the senary system is that they are entirely resistive towards the division by 4, which is probably the division that is most common as 3.
What Is a Numeral System?
A symbolic system that is used to express an array of digits in a constant fashion is known as a numeral system.
In mathematics, we commonly use the base 10 numeral system, but throughout the world, the most common numeral system used is the Arabic-Hindu numeral system. This system first originated in the sub-continent, and it is considered to be the basis for the development of the base 10 system.

Figure 2 – Some common Numeral Systems in the world
A number in one numeral system may possess different meanings in a different numeral system. Such as the number ‘11’, which in decimal numbering is simply eleven, but in a binary system, it is responsible for representing the decimal digit 3.
A number system is somewhat different from a numeral system, which is a system of expressing numbers in different forms. It gives a distinctive illustration of every number and depicts the construction of arithmetic and algebraic expressions.
The Senary Numeral System
The senary system consists of 6 numerals as a standard set which is given by D6 = {0, 1, 2, 3, 4, 5}. Every digit in the senary set is related to each other in the following linear manner 0 < 1 < 2 < 3 < 4 < 5.
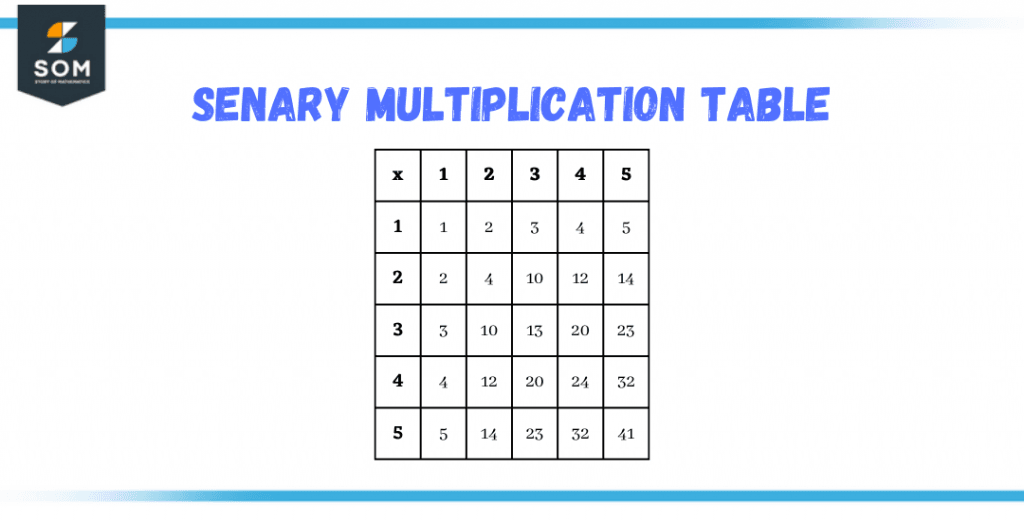
Figure 3 – Multiplication table in 6-digit Senary numeral system
When all the prime numbers except 2 and 3 are represented in the senary, they will have 1 or 5 as their last digit. A few prime numbers in senary are written as:
2, 3, 5, 11, 15, 21, 25, 31, 35, 45, 51, 101, 105, 111, 115, 125, 135, 141, 151, 155, 201, 211, 215, 225, 241, 245, 251, 255, 301, 305, 331, 335, 345, 351, 405, 411, 421, 431, 435, 445, 455, 501, 515, 521, 525, 531, 551
If the prime numbers are greater than 3, then the modular arithmetic operation comes in handy, where the final digit is either a 1 or a 5. This means whenever a prime number is divided by 6, the remainder is either 1 or 5.
In addition, each perfect number is represented in form 2$^{p-1}$(2$^p$ – 1) where (2$^p$ – 1) represents a prime number. Thus besides 6, every other perfect, consistent number will consist of 44 as the last two numbers in the senary system. Also, being the largest base of numbers, the multiplication table makes up a huge chunk compare to its size, which helps in memorizing the products and requires less effort.
A number will contain 3 digits 0, 2, and 4 as their last numbers when it is divided by 2 in senary. Similarly, a numeral will contain 2 digits 0 and 3 as their last numbers when it is divided by 3 in the senary.
How To Count Senary Numbers
It’s relatively easy to count senary numbers but not as much as compared to decimal numbers. Where one hand can be used to count the numbers, the other one is used as a specific position, such as the left hand being used as a unit counter, whereas the right hand is used to count the sixes.
Let’s say you hold out 3 fingers of your left hand and 4 fingers of your right hand, which is equivalent to 34senary in senary but 22decimal in decimal. The math behind this counting is quite straightforward, 3 x 6 + 4 = 22 in decimal, but the only drawback is that you can only count from zero to 35 in decimal or 55 in senary.
Apparently, this method is the least ideational manner to count since it represents the notions of positional notation, in which you move from one hand to the other hand. Preferably the left hand is used for units and the right for sixes, but it’s up to the counter which hand he or she prefers for the respected role.
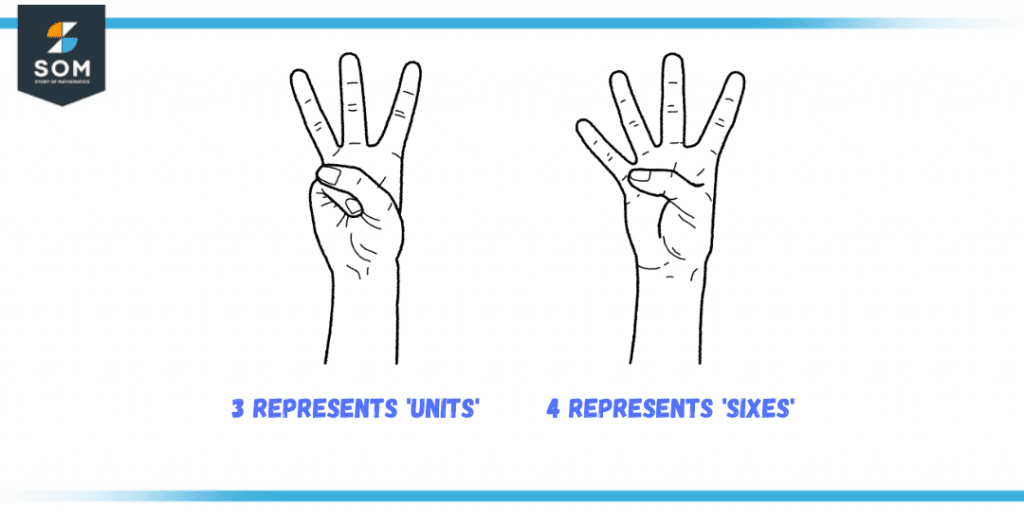
Figure 4 – A visual representation of finger counting in Senary
Solved Examples of Senary Numeral System
Example 1
Convert 1206 (senary) to base 10 (decimal).
Solution
This problem can be solved in two steps. Firstly we will start with the units place in 120.
Multiply units place with 60, then the tens decimal with 61, and finally the hundredth decimal with 62 and keep on going as many decimals as there are.
The next step is to add all the products that we just discussed above, which will be the equivalent of 120 in decimal.
Applying these steps to get our final answer for converting 120senary to decimal:
Decimal of 0 = 0 x 60 = 0
Decimal of 2 = 2 x 61 = 12
Decimal of 1 = 1 x 62 = 36
Adding all gives us the decimal of 120 = 36 + 12 + 0 = 48.
Thus 48 is the decimal equivalent of 120senary.
Example 2
Convert 48010 (decimal) to base-6 (senary).
Solution
The first step is to divide the whole number by 6, with each remainder and quotient being noted down. The division needs to be completed until the number is not further divisible by 6.
Finally, the answer can be achieved by assembling all the remainder in reverse order (down to up).
Applying these steps to get our final answer for converting 480decimal to senary.
Divide 480 by 6, giving 80 with the remainder 0.
Divide 80 by 6 gives 13, with the remainder 2.
Divide 13 by 6, giving 2 with the remainder 1.
Divide 2 by 6 gives 0 with the remainder 2.
Now writing the remainder from down to up format, we get the senary form of 48010 which is 21206.
All images are created using GeoGebra.
