Slope|Definition & Meaning

Figure 1 shows two lines with different slopes. Line B has a greater slope as it is steeper than line A.

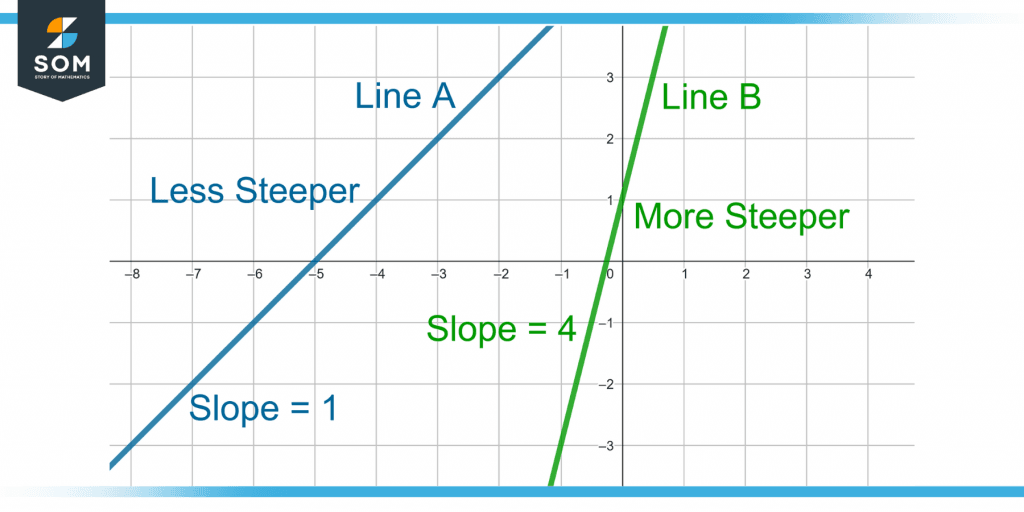
Figure 1 – Two Lines A and B with Different Slopes

Line

A line is a one-dimensional object which is infinitely long and has no width, depth, or curvature. It is made with an infinite number of points extending in opposite directions. The points lying on the same line are known as collinear points. 

Calculating the Slope of a Line

Two points (x₁, y₁) and (x₂, y₂) are required to find the slope of a line. The difference between the y-coordinates gives the rise(vertical change), and the difference between the x-coordinates gives the run(horizontal change).

Dividing the rise by run gives the slope “m” of the line as:

m = rise/run = (y₂ – y₁)/(x₂ – x₁)

For example, given two points (1, 2) and (3, 5) of the line, here:

x₁ = 1, y₁ = 2, x₂ = 3, y₂ = 5

Calculating the slope gives:

m = (5 – 2) / (3 – 1) = 3/2

Slope in Trigonometry

The slope m of a line can also be defined as the tangent of the angle θ that the line makes with the x-axis. Hence,

m = tan θ

Where θ lies between -90° and 90°. If the slope is known, the value of θ can be calculated by using the equation:

θ = tan^-1 (m)

For example, if a line’s slope is 10, the angle θ will be:

θ = tan^-1 (10) = 84.3°

Infinite and Zero Slope

A vertical line has an infinite slope, and a horizontal line has a zero slope. An undefined slope means that with no change in x-values, there is a change in y-values. A zero slope means that no change occurs in y-values for changing x-values.

Positive and Negative Slope

A positive slope means that a line moves in the upward direction from left to right. The y-values increase with increasing x-values.

A negative slope of a line means that y-values decrease with increasing x-values. The line goes in a downward direction from left to right.

Figure 2 shows lines with zero, infinite, positive, and negative slopes.

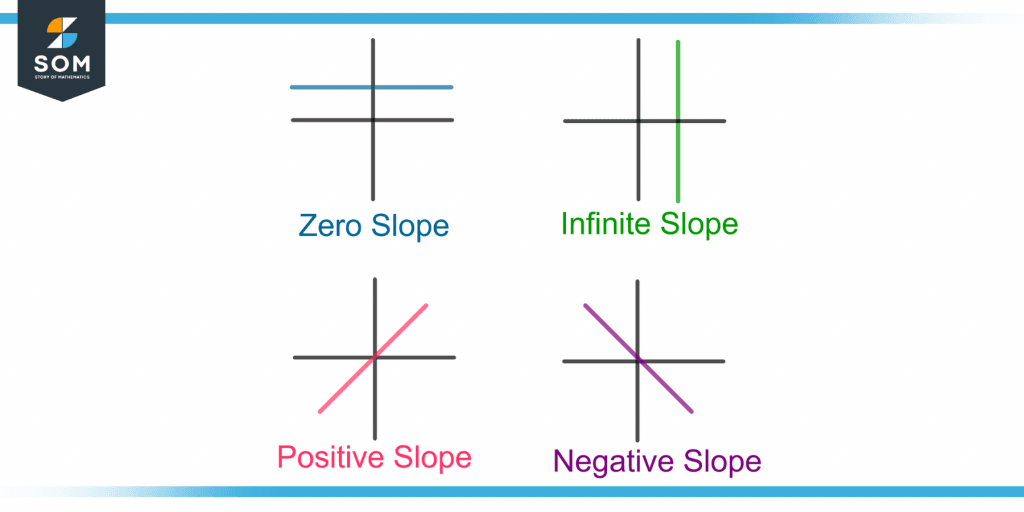
Figure 2 – Demonstration of Zero, Infinite, Positive, and Negative Slopes

Different Forms of Equations of a Line

The equation of a line is known as a linear equation having a degree of one. The following are three different ways to represent a linear equation.

Standard Form

A linear equation’s standard form of two variables, x and y, is:

Px + Qy = R

Where “P” and “Q” are the coefficients of the variables x and y, respectively, and R is a constant. For example, the equation 2x – 3y = 9 is in standard form.

Slope-intercept Form

A line’s slope-intercept form is given as

y = mx + a

Where “m” is the line’s slope, and “a” is the y-intercept.

For example, if a line’s slope is 2 and the y-intercept is -1, its slope-intercept form will be:

y = 2x – 1

The y-intercept is the value of y at the point (0, a) where the line crosses the y-axis. It can be found by placing x = 0 in the linear equation and solving for y.

The standard form can be converted into the slope-intercept form by rearranging the equation. For example, to convert the equation:

x + 2y = 8

into slope-intercept form, subtracting x on both sides gives:

2y = 8 – x

Dividing by 2 into both sides gives:

y = 4 – (1/2)x

Hence, the slope-intercept form is:

y = – (1/2)x + 4

Graphing a Line Using Slope-Intercept Form

The slope-intercept form provides the two essential parameters to graph a line, i.e., the slope and the y-intercept. Consider the equation:

y = (1/2)x + 4

The slope of the line is 1/2, and its y-intercept is 4.  A slope of 1/2 means a rise of 1 and a run of 2. A positive slope means that the rise will be in the upward direction from left to right.

Figure 3 shows the line obtained by using the slope-intercept form.

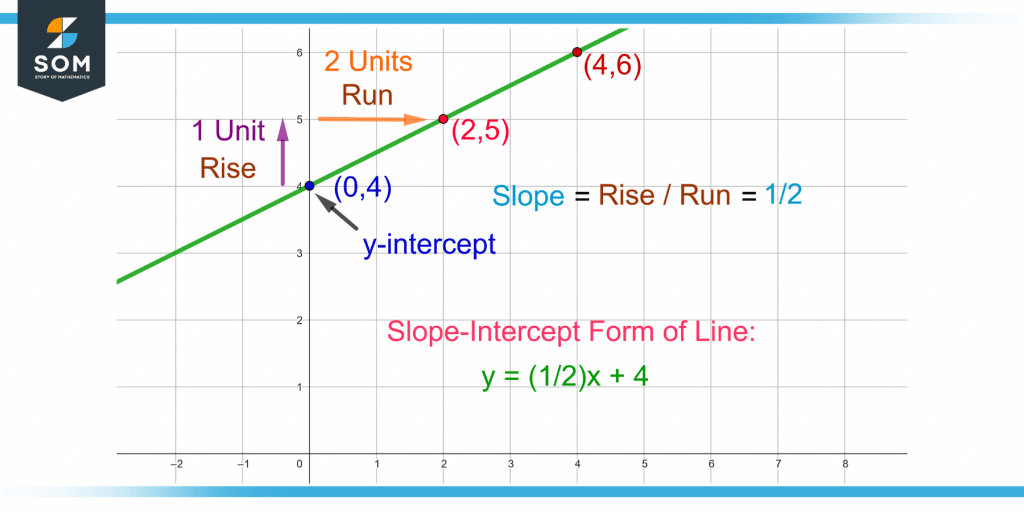
Figure 3 – Graphing a Line Using the Slope-intercept Form of a Line

Starting from the y-intercept 4, i.e., the point (0,4) and moving 1 unit up(rise) and 2 units right(run), the point reached is (2, 5). A line can be drawn by joining the two points (0, 4) and (2, 5) and extending the ends infinitely.

Point-slope Form

A line’s point-slope form is given as:

y – y₁ = m(x – x₁)

Where x₁ and y₁ are the x and y-coordinates of a point on the line. The point-slope is used to find a line’s equation when a point (x₁, y₁) on the line and its slope are given. It is also used when two points are given with which slope can be calculated.

Derivation of Point-slope Form

The point-slope form is derived from the slope-intercept form. Figure 4 shows a line having any points (x₁, y₁) and (x, y) on it.

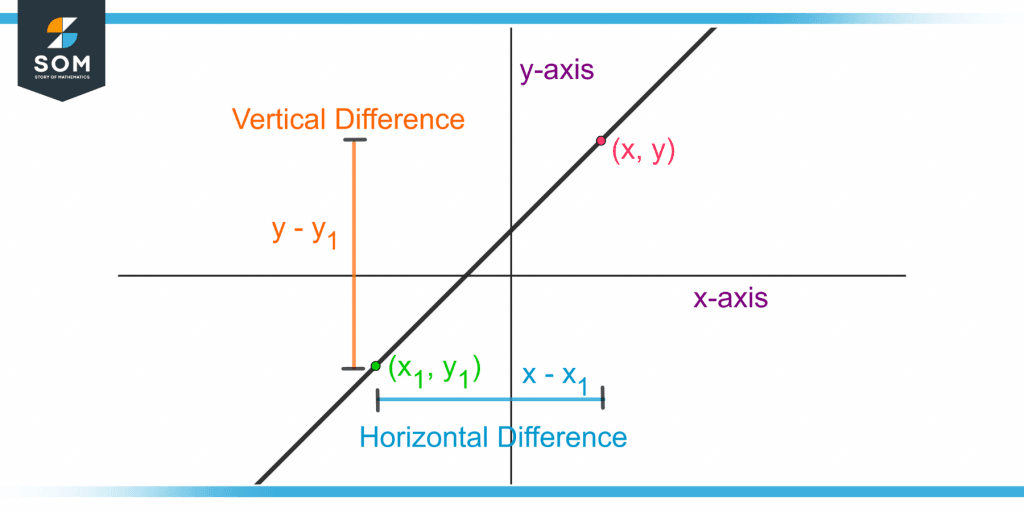
Figure 5 – Demonstration of Two Points on a Line and their Horizontal and Vertical Difference

For the point (x, y), the slope-intercept form is:

y = mx + a

For the point (x₁, y₁), the slope-intercept form is:

y₁ = mx₁ + a

Subtracting y₁ from y gives the vertical difference as:

y – y₁ = (mx + a) – (mx₁ + a)

y – y₁ = mx + a – mx₁ – a

y – y₁ = mx – mx₁

Taking m as common gives the point-slope form:

y – y₁ = m(x – x₁)

Slope of Two Parallel Lines

Two lines are parallel if and only if their slopes are equal. For example, the two lines:

y = 3x + 2 and y = 3x – 5

are parallel as both have the same slope, i.e., 3 as shown in figure 5.

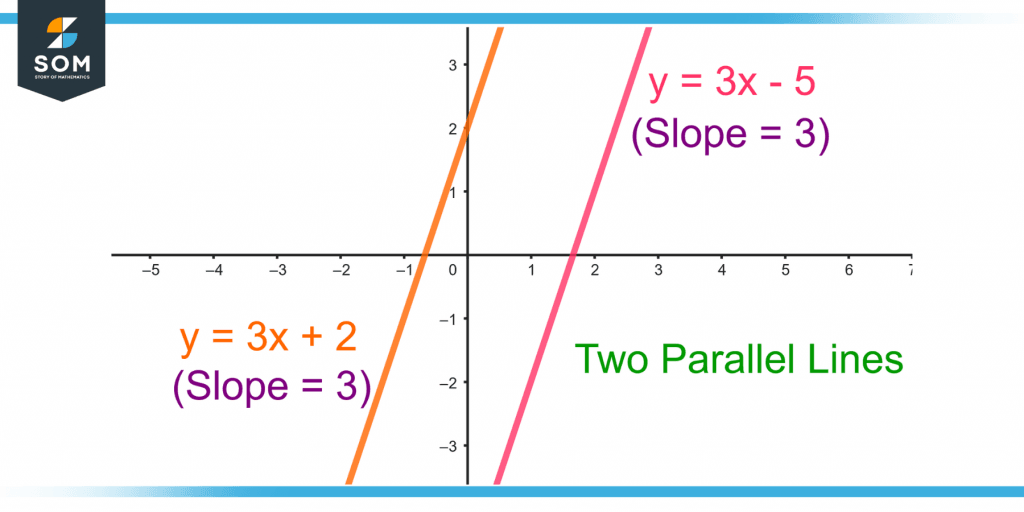
Figure 5 – Demonstration of Slopes of Two Parallel Lines

Slope of Two Perpendicular Lines

Two lines are perpendicular to each other if the product of their slopes is -1. For example, the two lines:

y = (-1/2)x – 3 and y = 2x + 1

have the slopes m₁ = -1/2 and m₂ = 2 respectively. The product of their slopes gives:

m₁.m₂ = (-1/2)(2) = -1

Hence, the two lines are perpendicular, as shown in figure 6.

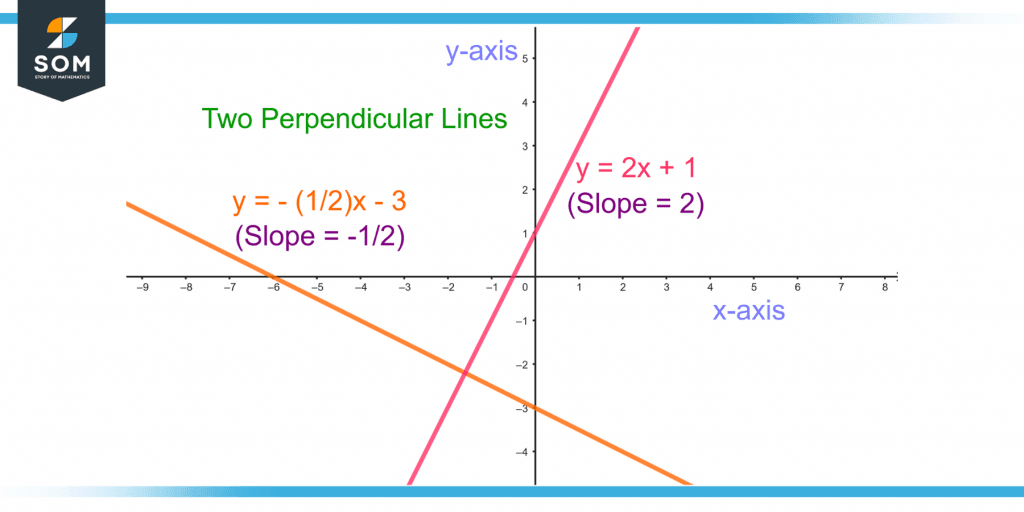
Figure 6 – Demonstration of Slopes of Two Perpendicular Lines

A line with a zero slope is also perpendicular to a line with an infinite slope.

Slope of a Function

The slope at a point (l, m) on the function’s curve can be found by taking its first derivative and finding its value by substituting the point (l, m). For example, the function:

y = x³

has the first derivative as:

dy/dx = d(x³)/dx = 3x²

To find the slope at the point (2, 3) on the function, substituting (2, 3) in the first derivative gives:

dy/dx at P(2, 3) = 3(2)² = 3(4) = 12

Hence, the slope at the point (2, 3) is 12.

Exponential Function

The exponential function e^x has the first derivative as:

dy/dx = d(e^x)/dx = e^x

The function f(x) = e^x is a special function as it is the only function whose slope at each point on the curve is equal to the value of the function at that point. For example, at x = 1, the function’s value is:

f(1) = e¹ = e ≈ 2.178

which is also the slope of the curve at the point (1, e), as shown in figure 7.

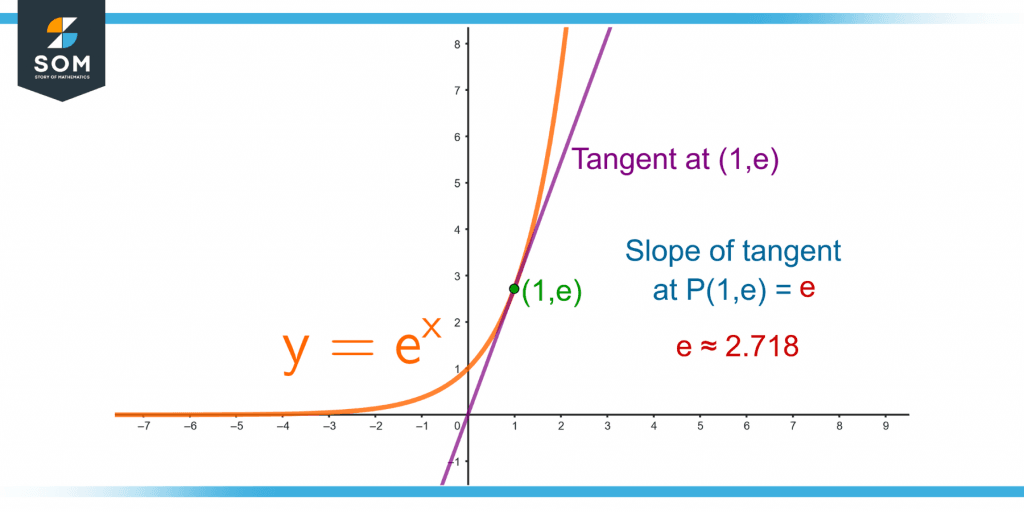
Figure 7 – The Exponential Function and its Slope at the Point (1, e)

A function’s curve has a varying slope at each point. A tangent line is drawn at the point to find the slope at that point on the curve. This tangent line’s slope gives the curve’s slope at that point.

Examples Related to Slope

Example 1 – Finding the Slope of a Line

Given two points (0, 0) and (5, -2) on the line, find the slope.

Solution

Slope = (y₂ – y₁) / (x₂ – x₁) = (-2 – 0) / (5 – 0) = -2/5

Example 2 – Using the Slope-intercept Form

A line has a slope of -1 and a y-intercept of 2. Find the equation of the line and graph the line.

Solution

As the slope and y-intercept are given, the slope-intercept form of a line is:

y = mx + a

Here,

m = -1 and a = 2

Putting the values gives the equation as:

y = (-1)x + 2

y = – x + 2

The slope is -1 with a rise of -1 and a run of 1. To graph the line, starting from point (0, 2) and moving 1(rise) unit down(as the slope is negative) and 1(run) unit left. The point reached is (1, 1).

Joining the two points (0, 2) and (1, 1) and extending them in the opposite direction is the required line, as shown in figure 8.

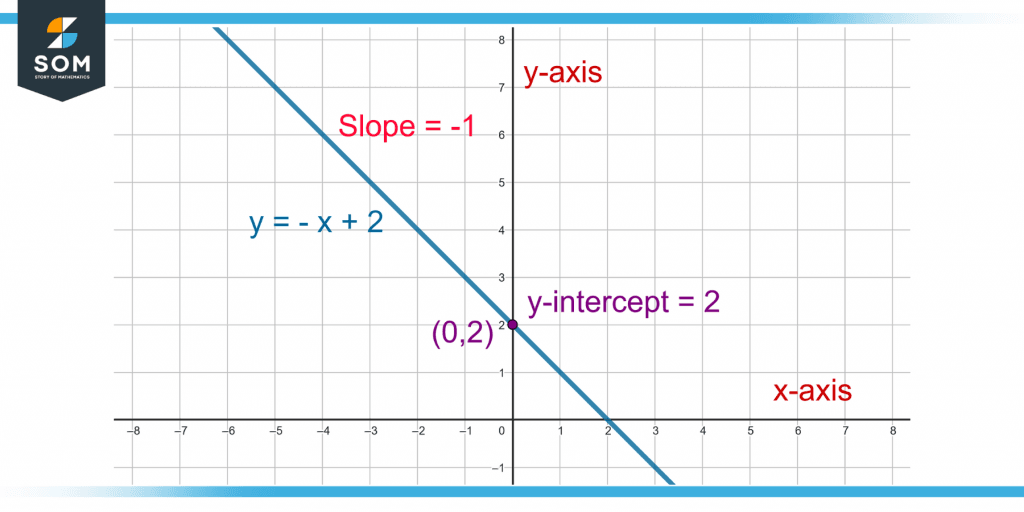
Figure 8 – Graphing a Line Using Slope and y-intercept

Example 3 – Using the Point-slope Form

Find the equation of a line given the slope as -2 and a point (5, 0) that goes through the line. Also, convert the equation into standard form.

Solution

As the slope and a point are given, the point-slope form is:

y – y₁ = m(x – x₁)

Here,

(x₁, y₁) = (5, 0) and m = -2

Putting the values in the above equation gives:

y – 0 = -2(x – 5)

y = -2x + 10

Adding 2x on both sides to convert the above equation in standard form as:

2x + y = 10

All the images are created using GeoGebra.

Slide Definition < Glossary Index > Solid Definition