Tangent Line|Definition & Meaning

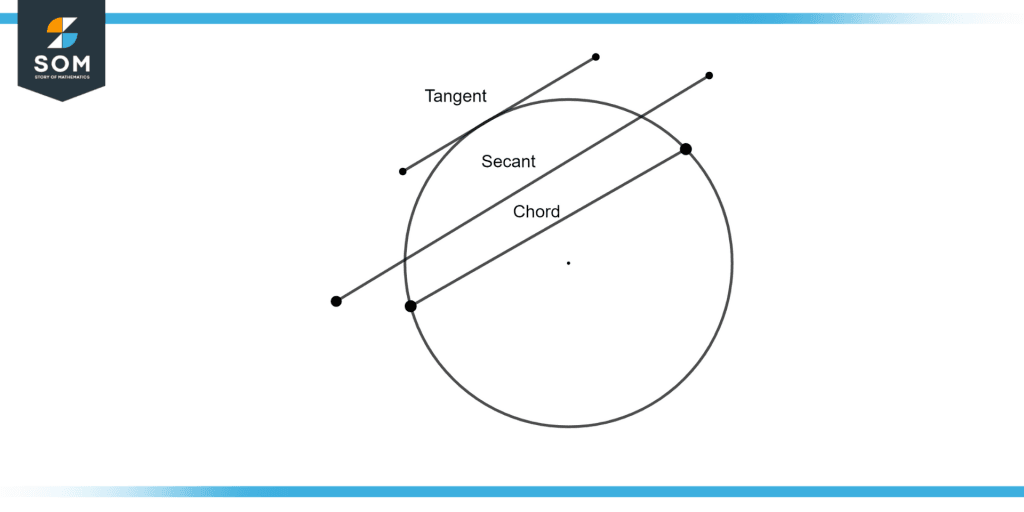
Figure 1 – Difference between Tangent Secant and Chord

Figure 1 illustrates the difference between tangent, secant line, and chord. 

A subfield of mathematics called geometry examines the dimensions, placements, angles, and sizes of objects. 2D forms, which include flat shapes like squares, circles, and triangles, are a subset of flat geometry. The length and breadth are the only 2 dimensions of these forms. Open and closed forms are additional categories for 2D shapes.

A form or figure that has unmet line segments and/or curves is referred to be an open shape. Their beginning and end do not coincide. Geometric forms that start and terminate at the same location are said to be closed shapes.

A solid figure, object, or form with three dimensions length, breadth, and height, is referred to as a three-dimensional shape in geometry. Three-dimensional forms contain thickness or depth, in contrast to two-dimensional shapes. In terms of geometry, an angle is the shape created when two rays intersect at a single terminal. The sign is used to denote an angle.

A line that barely touches the function’s graph at a given position and is “parallel” (in some sense) to it is said to be tangent to the function at that location.

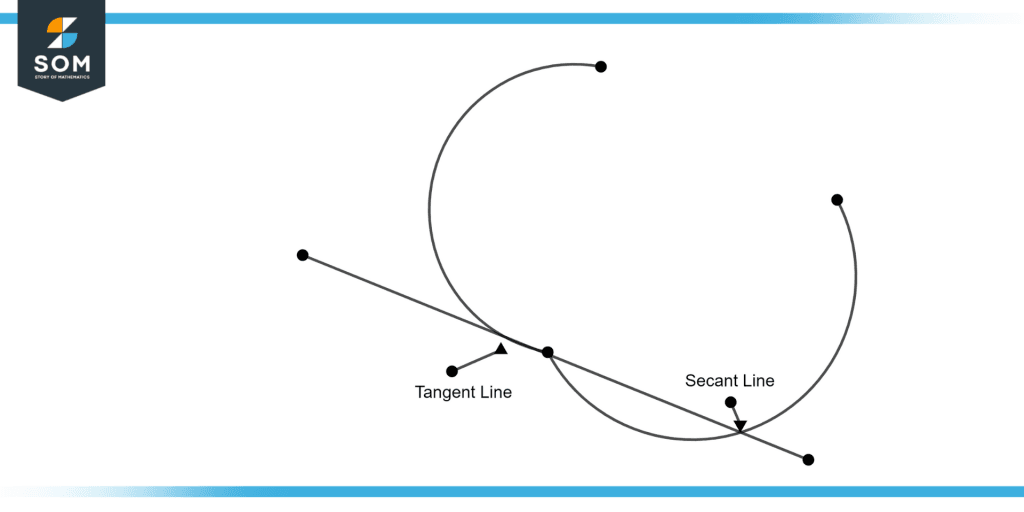
Figure 2 – Tangent and Secant Line

Figure 2 illustrates the tangent and secant lines.

“Tangent line” distinction is one of its most important applications. The word “tangent” has its roots in the Latin verb “tangere,” which meaning “to touch.” The tangent line makes contact with the curve at a certain location on the curve. Since the equation of the curve is supplied by a function, we must also know the point at which the tangent is drawn in order to obtain the tangent line equation.

In the 1630s, Fermat created the adequality approach, which he utilized to solve various analysis-related issues and compute tangents to parabolas. Comparable to taking the difference between f(x+h) and f(x) and dividing by a power of h is the inequality approach. Descartes independently employed his normal approach based on the finding that a circle’s radius is always normal to the circle itself.

Slope of a Tangent Line

The slope of a tangent line is nothing but the derivative of the function f(x), as illustrated in figure 3:

Figure 3 – Slope of a tangent line and the definition of the derivative (slope).

Tangent Line Equation

To determine the equation of the tangent line to a curve with the equation y = f(x) drawn at the point (x₀, y₀) (or at x = x₀):

Step 1: If the y-coordinate of the point is not specified, substitute it into the function y = f(x) to find the y-coordinate of the point, i.e., if the question states that the tangent is drawn at x = x₀ .

Specifically, y-coordinate, y₀ = f (x₀).

Step 2: Calculate the derivative of the function y = f(x) and use the symbol f’ to denote it (x).

Step 3: Replace the point (x₀, y₀) in the derivative f'(x) to obtain the tangent’s slope (m).

Step 4: Using the point-slope form y – y₀ = m, get the equation of the tangent (x – x₀).

The equation of the tangent line is all that is necessary to understand the idea of linear approximation. In other words, using the formula for the tangent of the function y = f(x) at the point (x₀, y₀), ( x₀, y₀).

The formula y – y₀ = m (x – x₀), where m = (f ‘(x)), is used to get the equation for the tangent line of a curve at a point (x₀, y₀) (x₀, y₀). The tangent slope is m = tan$\theta$ if $\theta$ is the angle it makes with the positive x-axis direction.

The slope of the normal is equal to (-1) divided by (the slope of the tangent). As horizontal tangents are parallel to the x-axis, a curve with the equation y = f(x) has horizontal tangents at the places where f'(x) = 0. As horizontal tangents are parallel to the y-axis, a curve with the equation y = f(x) contains vertical tangents at the places where f'(x) is undefinable.

The estimated values of the function near the place where the tangent is drawn are determined using the tangent line equation.

Some Examples of Tangent Line

Example 1

Find the slope of the tangent line of value $\sqrt[3]{8}$.

Solution

Now:

(x₀, y₀)=(8, 2)

In order to evaluate the derivative of the function $\sqrt[3]{x}$, which can be solved by the power rule, which is:

$\dfrac{1}{3}$ $x^{-0.667}$

 and the value of the x is equal to 8, so:

$\dfrac{1}{3}$ $8^{-0.667}$

 so the slope of the tangent line is equal to:

$\dfrac{1}{12}$.

Example 2

Find the slope of the tangent line of value $\sqrt[3]{27}$.

Solution

You can see the slope of the tangent line is the derivative of the function. So we have a value which is $\sqrt[3]{27}$, which is equal to 3. Now we assume that the function f(x), which is $\sqrt[3]{x}$, and where the tangent is drawn to be x₀ is equal to 27.

Now

(x₀, y₀)=(27, 3)

In order to evaluate the derivative of the function $\sqrt[3]{x}$, which can be solved by the power rule, which is:

$\dfrac{1}{3}$ $x^{\frac{-2}{3}}$

 and the value of the x is equal to 8, so:

$\dfrac{1}{3}$ $27^{\frac{-2}{3}}$

 so the slope of the tangent line is equal to:

0.0378

Example 3

Find the slope of the tangent line of value $\sqrt[3]{125}$.

Solution

You can see the slope of the tangent line is the derivative of the function. So we have a value which is $\sqrt[3]{125}$, which is equal to 5. Now we assume that the function f(x), which is $\sqrt[3]{x}$, and where the tangent is drawn to be x₀is equal to 125.

Now:

(x₀, y₀) = (125, 5)

In order to evaluate the derivative of the function $\sqrt[3]{x}$, which can be solved by the power rule, which is:

$\dfrac{1}{3}$ $x^{\frac{-2}{3}}$

The value of the x is equal to 8, so:

$\dfrac{1}{3}$ $125^{\frac{-2}{3}}$

So the slope of the tangent line is equal to:

0.0134

All images were created using GeoGebra.

Table Definition < Glossary Index > Tangram Definition