Solution|Definition & Meaning

Overview of Solution

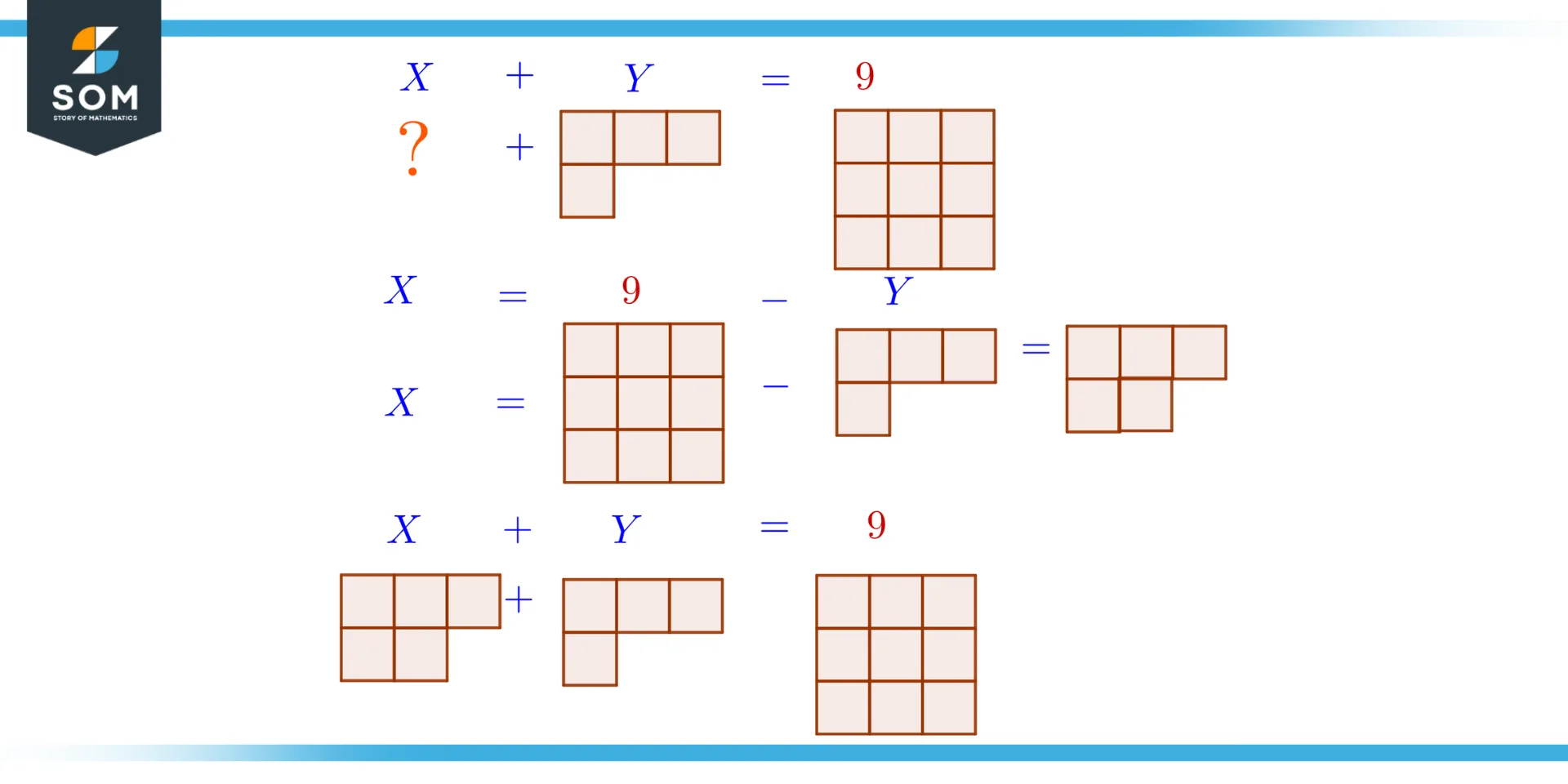
Figure 1 – Overview of solution

Suppose a scenario where we have two variables and one of them let’s say x represents four boxes and y represents an unknown number of boxes, both of the variables sum up to give a total of 9 boxes. We can write this problem in equation form as:

x + y = 9

As y = 4

4 + y = 9

We want to find the solution to the equation by finding the value of y that satisfies the equation.

Rewriting the equation:

4 + y = 9

y = 9 – 4

y = 5

Putting in the original equation :

4 + (5) = 9

9 = 9

So the solution for the above equation that satisfies the equation is y = 5.

This is an example of an analytic solution, which is a solution that is expressed in terms of mathematical operations and functions. In this case, the solution was found by performing algebraic operations on the equation to isolate the variable y. 

Methods for Solution

There are many different methods that can be used to solve equations and systems of equations, depending on the type of equation and the complexity of the problem. Some of the most common methods include graphing, substitution, elimination, and factoring.

Graphing Method

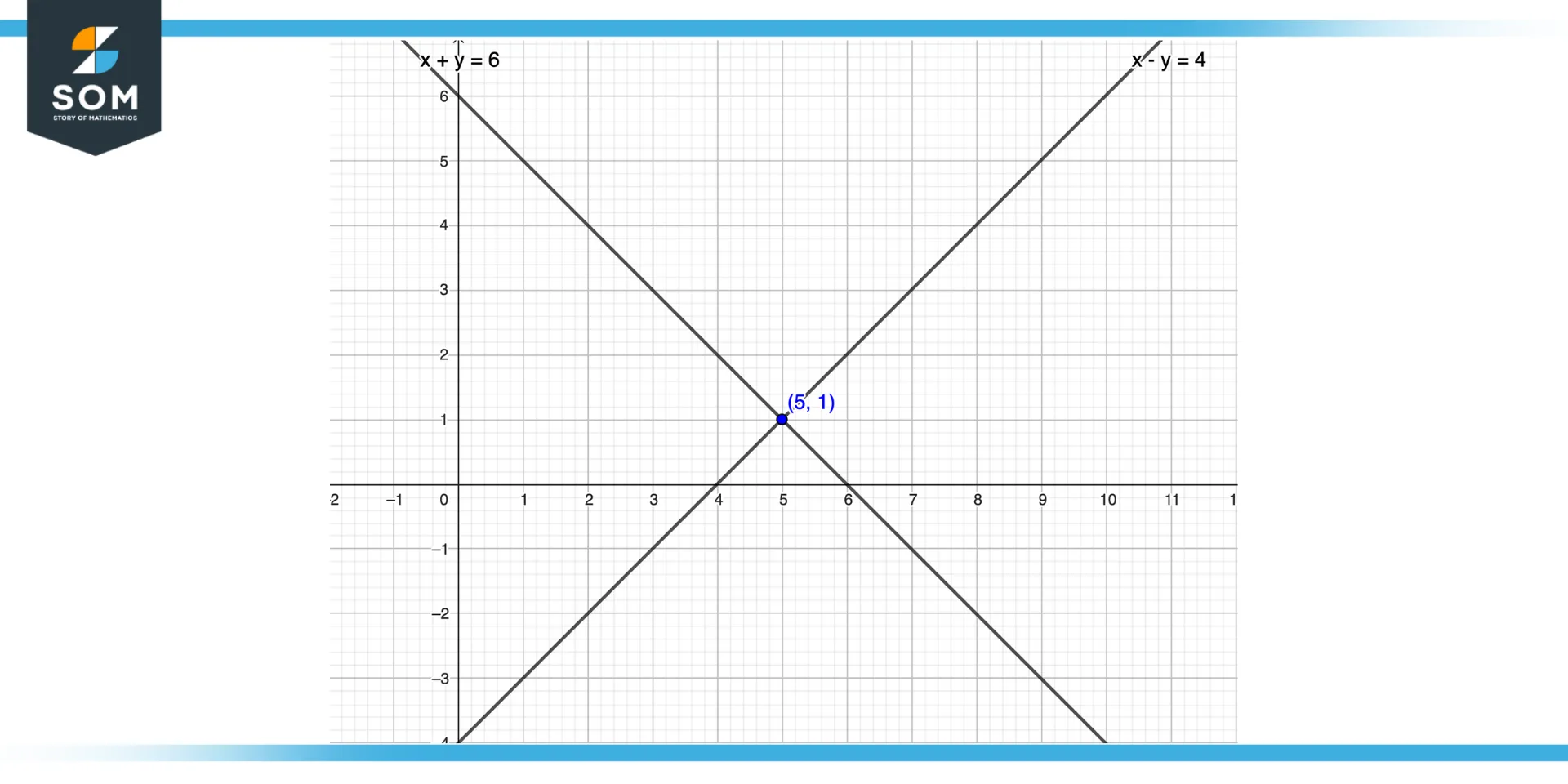
Figure 2 – Solution of equations through the graphical method

A technique for solving linear equations and systems of linear equations is graphing. In order to solve an equation by graphing it, one must first plot the equation on a coordinate plane and then search for the locations where the x or y-axis intersects the equation. The equation’s solutions are represented by these points.

Substitution Method

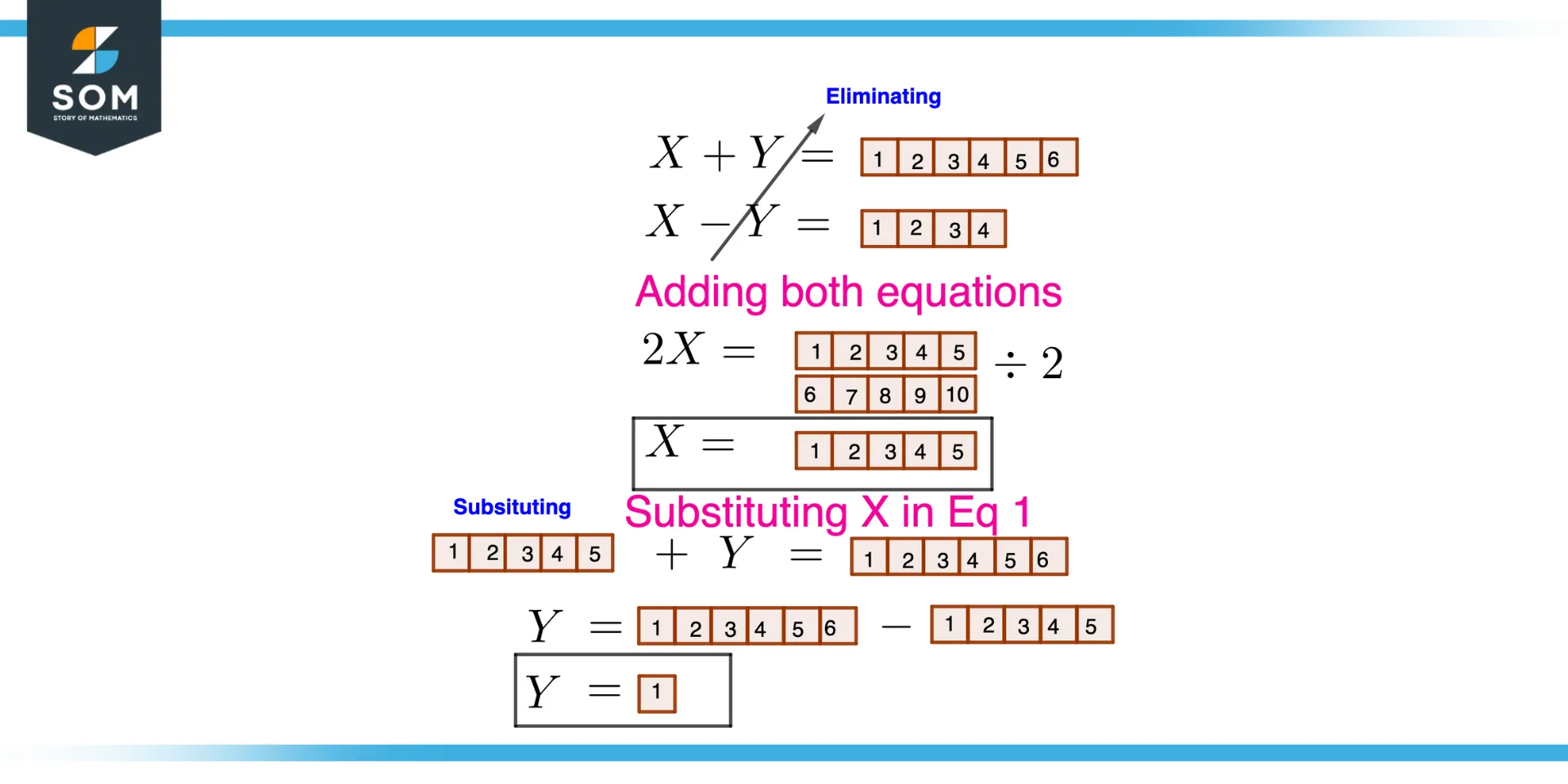
Figure 3 – Eliminating and Substituting to get the solution of the equation

A technique for solving linear equations and systems of linear equations is substitution. When using substitution to solve an equation, we first answer one equation for each variable in terms of the other equation, and then we insert this solution into the different equation. This enables us to solve for the other variable while also removing one of the variables.

Elimination Method

Systems of linear equations can be solved using the elimination technique. In order to eliminate one of the variables from a system of equations, we add or subtract the equations, and then we solve for the remaining variable. This approach is comparable to substitution, but in some circumstances, it may be more effective.

Factoring Method

Polynomial equations can be solved using the factoring technique. We first construct the equation in standard form, with the highest-order term on the left and the constant term on the right, in order to factor the equation. The left side of the equation is then attempted to be factored into the sum of the two polynomials. In the event that we are successful, we can next resolve the equation by putting all of the factors at zero and calculating the roots.

Types of Solution

There are several types of solutions in mathematics:

Analytic Solutions

Solutions that can be described in terms of mathematical operations and functions are referred to as analytical solutions. Typically, equations or systems of equations must be solved in order to find an analytical solution.

Numerical Solutions

These are solutions that have been roughly calculated using numerical techniques like finite differences or Monte Carlo simulations. When analytic solutions are either not possible or too hard to find, numerical solutions are frequently used.

Graphical Solutions

Visually portrayed solutions, such as graphs or diagrams, are referred to as graphic solutions. To illustrate relationships between variables or to see patterns and trends in data, graphical solutions can be utilized.

Exact Solutions 

Solutions that are exact, these are solutions that are exact and precise. As opposed to numerically estimating the solution, exact solutions are often found by solving equations or systems of equations.

Approximate Solutions

Solutions that are close enough to be useful but are not exact in nature are called approximate solutions. When an exact solution is not required or when it is too challenging to achieve an exact solution, approximate solutions are frequently utilized.

Implicit Solutions

Implicit solutions are those that are indicated by the situation or problem but are not stated clearly. Making assumptions about the issue or manipulating the available information can lead to the discovery of implicit solutions.

Steps to Find a Solution

To find the solution to an equation, you can follow these steps:

Identification of the Problem 

Identifying the problem that you seek to solve is the first step toward finding the solution. It is necessary to read the problem statement, identify the variables involved, and understand the context in which the problem is framed.

Define Goal 

Determine your goal after identifying the problem. In this case, it may be necessary to determine a relationship between variables, or to solve a particular unknown in order to find a value.

Gathering Information 

The next step is to gather any information or data that you will need to solve the problem. You may need to gather data, identify equations and formulas, or make assumptions about the problem.

Identification of the Equation 

To determine the solution to an equation, you must identify the equation that describes the problem. An equation can be formed by using formulas or relationships or manipulating the problem conditions.

Solving the Equation

Now that you’ve found the equation that describes the problem, you can use algebraic techniques to solve it. Methods such as factoring, completing squares, and quadratic formulas can be used.

Verifying Your Solution 

Once you have come up with a solution, you should verify that you have come up with a reasonable and accurate solution. Test your solution with additional data or verify that it meets the problem conditions.

Communicating Your Results 

Be concise and clear with your results, using appropriate language and notation. 

Solved Examples

Example 1

For example, consider the equation 2x + 5 = 9. Find the solution.

Solution

To solve this equation, you could follow these steps:

1. Identification of the problem: You are trying to find the value of x that makes the equation 2x + 5 = 9 true.
2. Define Goal: You are trying to find the value of x.
3. Gathering information: You are given the equation 2x + 5 = 9.
4. Identification of the equation: This is the equation you are trying to solve.
5. Solving the equation: You can use algebraic techniques to isolate the variable x on one side of the equation. In this case, you can subtract 5 from both sides of the equation to get 2x = 4. Then, you can divide both sides of the equation by 2 to get x = 2.
6. Verifying your solution: You can check your solution by substituting x = 2 back into the original equation to verify that it is a valid solution.
7. Communicating your results: You can communicate your results by stating that the solution to the equation is x = 2.

Example 2

Consider three circles as variable y and unknown circles as variable x that are added to give the result of 9. Find the solution of the equation that satisfy the equation.

Solution

The exact solution to the problem is shown below.

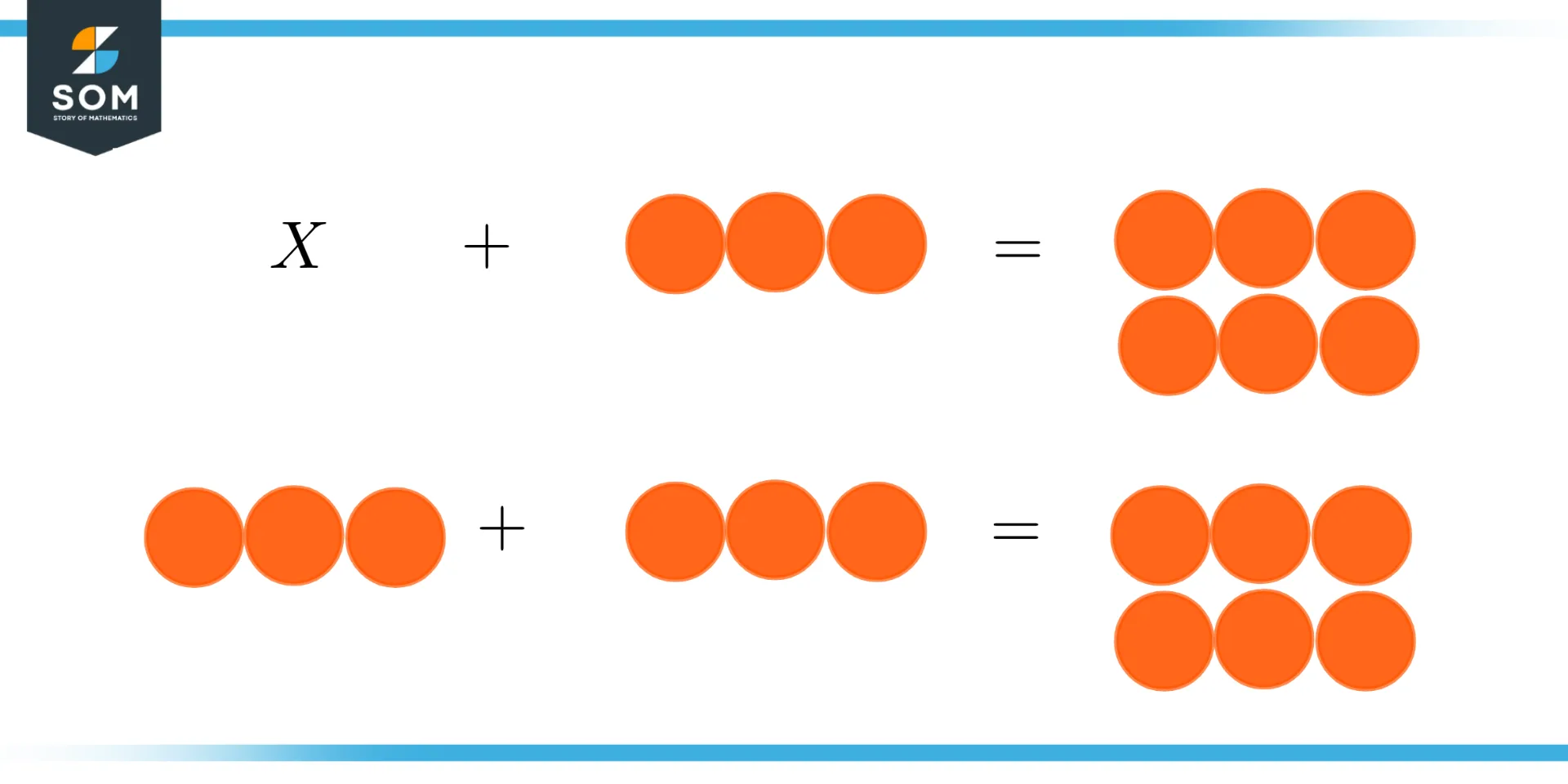
Figure 4 – Example of the exact solution

So the exact solution that satisfies the equation is x = 3.

All mathematical drawings and images were created with GeoGebra.

Solid Definition < Glossary Index > Solve Definition