Solve|Definition & Meaning

Figure 1 below shows the solution where the left-hand side is equal to the right-hand side.

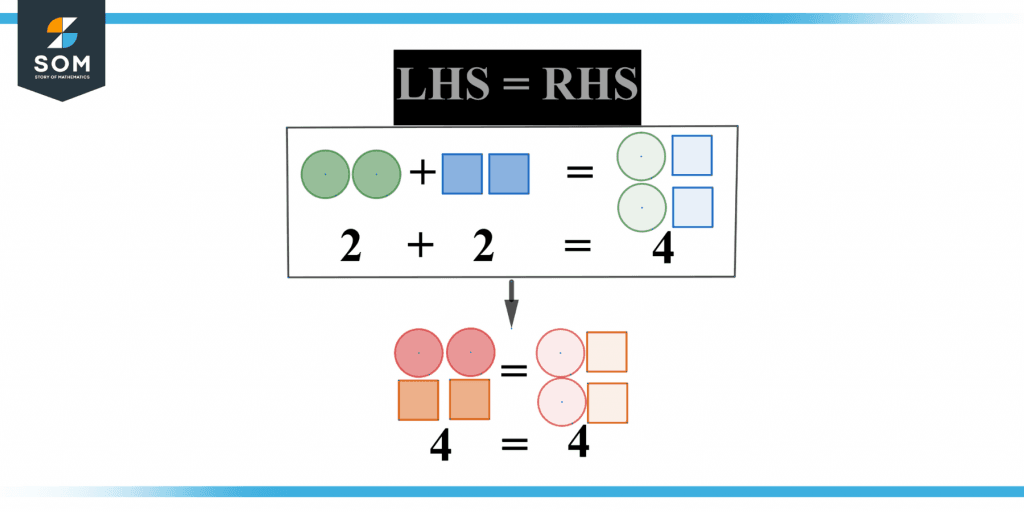
Figure 1 – Representation of LHS and RHS.

To Solve the Equations

The process of solving equations entails determining the value of an unknown element in the given formula. The value for the variable satisfies the criterion that the two alternatives are equal.

A linear equation with one variable has a single solution; a linear equation with two variables has two answers. When you solve a quadratic equation, you get two roots. When solving an equation, numerous approaches and processes are used. 

Solving equations entails calculating the value of an unknown variable while keeping the equation balanced on both sides. An expression is a variable condition in which two alternatives in the parameter have the same value.

The answer to the problem is the quantity of the parameter for which the solution is fulfilled. If the LHS & RHS of an equation are swapped, the equation stays the same. The variable whose value is to be determined is isolated, and the answer is achieved.

The sort of equation we are working with influences how we solve it. Quadratic, linear, radical, and rational equations are all examples of equations.

Figure 2 below shows the solution of an equation.

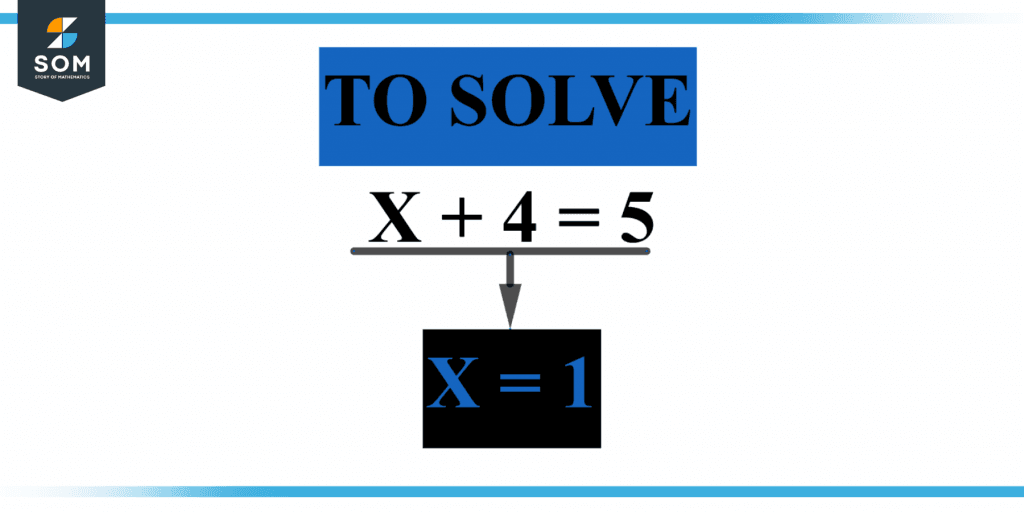
Figure 2 – Representation of solving an equation.

Methods for Solving Equations

The goal of solving an expression is to identify the values of parameters that make the equation’s condition true. To isolate the parameter, conduct the following actions while keeping the equation balanced on both sides. By doing so, LHS remains equivalent to RHS, and the equilibrium eventually remains unchanged throughout.

• The additional feature of equality states that you should add the same number to both sides. If x = y, x + z Equals y + z.
• Equality’s subtraction property: Take the same number off both sides. If x = y, x – z Equals y – z.
• Equality’s multiplication property: Multiply both sides by the same number. If x = y, xz Equals yz.
• Equality’s division property: On both sides, divide by the exact number. If an Equals b, then $\dfrac{x}{z}$ = $\dfrac{y}{z}$  (c = 0).
• Equality’s division property: On both sides, divide by the exact number. If an Equals b, then $\dfrac{x}{z}$ = $\dfrac{y}{z}$  (c = 0). Following this methodical balancing strategy of answering an expression using comparable mathematical functions across both sides of the expression, we separate the component into one side. The last process is the answer to the problem.

Following this methodical balancing strategy of answering an expression by a succession of comparable arithmetic on both aspects of the equation, we split the factor into one side, and the final step is indeed the result of the problem.

Figure 3 shows the methods of solving equations.

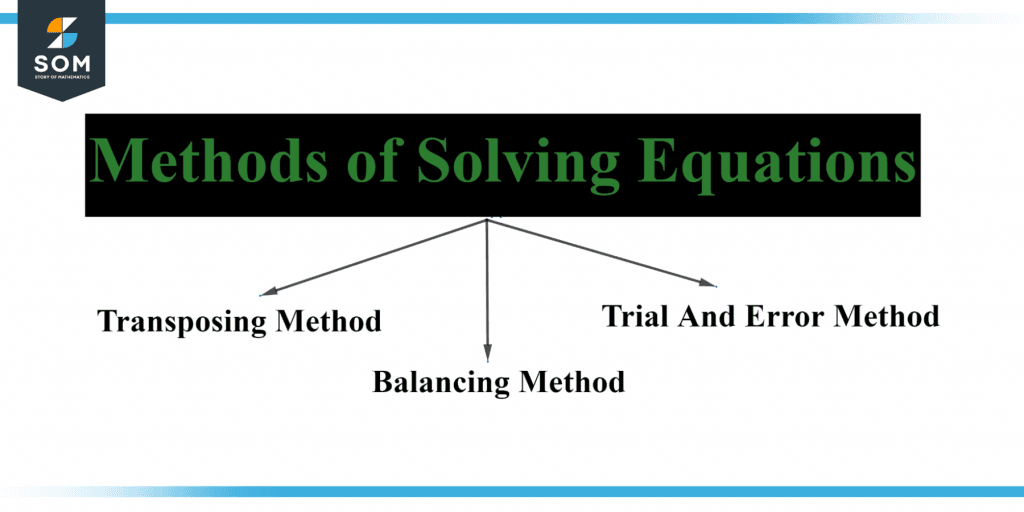
Figure 3 – Methods to solve an equation.

Solving Equations With a Single Variable

A one-variable linear equation of the form ax + b = 0, in which a, b, and c are real values. When solving a linear equation, the following stages are taken.

• If necessary, remove the parentheses and apply the distributive property.
• Combine comparable terms to simplify both sides of the problem.
• If the equation contains fractions, multiply all sides even by the least common denominator of each of the fractions.
• To convert decimals to whole numbers, multiply the equation’s sides by the smallest power of ten.
• Using the subtracting and adding properties of equality, move the variable parts to one side of the expression and the consistent terms to the other.
• To use equality’s multiplication and division characteristics, set the variable’s coefficient to 1.
• Find the solution by isolating the variable.

Using the Trial and Error Technique To Solve an Equation

Consider the expression 12x = 60. To determine x, we calculate 12 times whatever number equals 60. We discover that the needed number is 5. It is only sometimes straightforward to solve equations through trial and error.

Using the Balancing Method To Solve an Equation

To solve an equation, we must isolate the variable x. Let us solve it using the removal of variables approach or the balancing method. Consider the following equation: 

2x + 4 = 17

In the first stage, we remove three. To maintain the equation balanced when solving it, we deduct four from each of the sides. Therefore:

2x + 4 – 4 = 17 – 4

2x = 13

Using the Transposing Method To Solve an Equation

We shift the sides of the integers while solving an equation. This is known as transposing. We alter the sign of a number or reverse the action when transposing it. Consider the expression 5y + 2 = 22.

We must isolate y to discover it. As a result, we flip the value 2 to the opposite side. The formula becomes:

5y = 22 – 2

5y = 20

Taking 5 to the opposite side, we invert the multiplication to the division process. y Equals 20 divided by 5 equals 4.

Examples of Solving Equations

Below are some examples of solving the equations

Example 1

Solve the expressions 0.4(a+10) = 2 – 0.6a by transposing it.

Solution

The steps for solving linear equations with decimals are as follows.

Given that:

0.4(a + 10) = 2 – 0.6a

Solving for a:

0.4a + 0.4 × 10 = 2 – 0.6a

(0.4a) + 4 = 2 – 0.6a

(0.4a) + 0.6a = 2 – 4

a = -2

So the solution is -2.

Example 2

When calculating the equation 4 [(p – 3)] – (p – 5) = 5, figure out the value of p?

Solution

4 (p – 3) – 5 (p – 5) = 5

Let us solve equations using the transposing approach. Applying the distributive property:

4p – 12 – p + 5 = 5 

3p – 8 = 4

3p = 4 + 8

3p = 12

p = 4

The answer is that p equals 4.

All images are made using GeoGebra.

Solution Definition < Glossary Index > Speed Definition