JUMP TO TOPIC
Speed|Definition & Meaning
Definition
Speed defines the rate at which an object is traveling. An object covers a distance at some time with a certain speed. The speed determines how fast an object moves, given that it covers some distance. An object at rest has no speed.
Figure 1 shows a car moving at a certain speed from the initial point to the final point.
Figure 1 – A Car Moving With Some Speed
Speed’s Mathematical Formula
The time rate of change of distance covered by an object is known as speed. It can be expressed mathematically as follows:
Speed = Distance/Time
s = d/t
Where s is the speed of the object covering a distance d per time t, speed is also denoted by v sometimes as it is the magnitude of velocity. Distance and time play an important role in the discussion of speed.
Distance
Distance is a quantity that determines how much of a length an object has covered. It is denoted by “S” or “d”. It is measured in meters(m) in SI and also measured in kilometers(km).
Kilometers and meters are related as follows:
1 km = 1000 m
Similarly,
1 m = 1/1000 km = 0.001 km
A distance always has a starting point and a finishing point. It does not have a direction, hence is a scalar quantity. It is zero when the object is at rest.
Figure 2 shows two balls, one at rest and the other covering a distance from A to B.
Figure 2 – One Ball at Rest and the Other Covering some Distance
Time
Time is defined as the ongoing independent quantity that produces a change in conditions. Einstein called it relative to some frame of reference.
It is a passing fundamental quantity through which the change in all other quantities can be noticed.
Its System International unit is seconds(s) and is a scalar quantity.
It can also be measured in hours, minutes, days, months, years, etc. For speed, the time taken is usually in seconds and hours.
As:
1 hr = 60 min
1 min = 60 sec
So the relation between an hour and a second is:
1 h = 60 × 60 = 3600 s
Hour and seconds are also abbreviated as “hr” and “sec” respectively.
Units of Speed
The commonly used units of speed are as follows:
Meters per Second
The unit used for slower speeds is meters per second. It is also used when a small amount of distance is covered.
It is written as “m/s” and means that an object covers this many meters in one second.
For example, 30 m/s speed refers to an object covering 30 meters every second of the journey.
Kilometers per Hour
The second unit of speed is kilometers per hour. It is abbreviated as “km/h”.
The distance covered by vehicles on roads is in kilometers and it requires a lot of seconds to cover a few kilometers. That is why the unit hour is used with the kilometer.
It is defined as how many kilometers an object travels in an hour. For example, the speed of 100 km/h refers to covering 100 km in one hour.
Uniform and Non-uniform Speed
When an object covers the same amount of distance per time interval, its speed is uniform.
Non-uniform speed refers to an object covering an unequal distance in each time interval. Figure 3 shows the illustration of uniform and non-uniform speed.
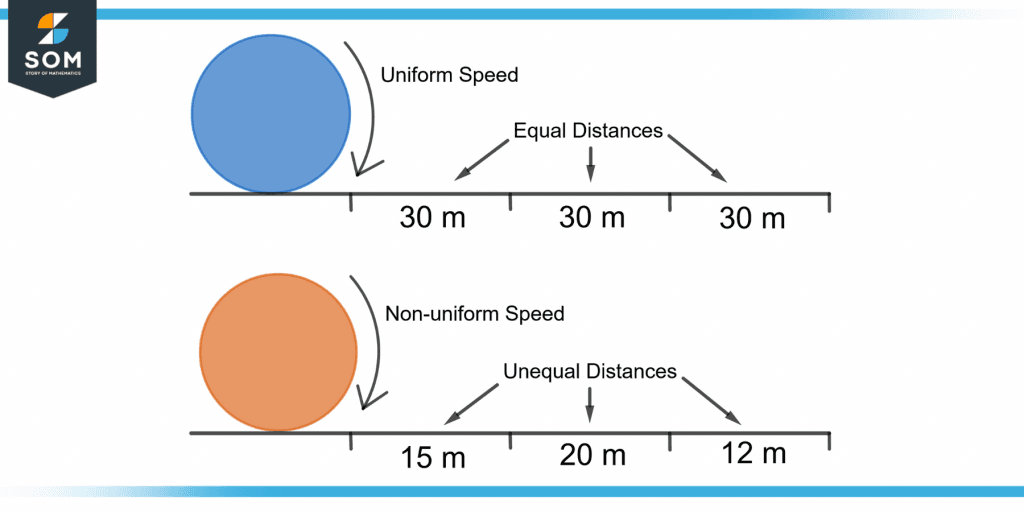
Figure 3 – Illustration of Uniform and Non-uniform Speed
Velocity
The speed with a direction is known as velocity. It has the same magnitude as speed, but it is a vector quantity.
Velocity is denoted by $\overrightarrow{v}$ and speed by v. The formula for velocity is the same as speed.
The direction is specified by using the words north, south, east, and west.
Acceleration
The change in velocity per unit of time is called acceleration. An object accelerates when it changes its velocity. It means that either or both its magnitude (speed) or direction can change.
The mathematical formula for acceleration a is:
a = v/t
It is measured in meters per second squared ($ms^{-2}$).
Speed-Time Graph
The speed-time graph shows the acceleration produced in an object. Time is the independent quantity and is taken on the x-axis.
The change in speed depends upon time; hence it is the dependent quantity and is taken on the y-axis. Two main cases arise while discussing the change in speed.
Case 1
When an object is moving with a constant speed, no acceleration is produced in the object.
Figure 4 shows the speed-time graph for an object moving with constant speed.
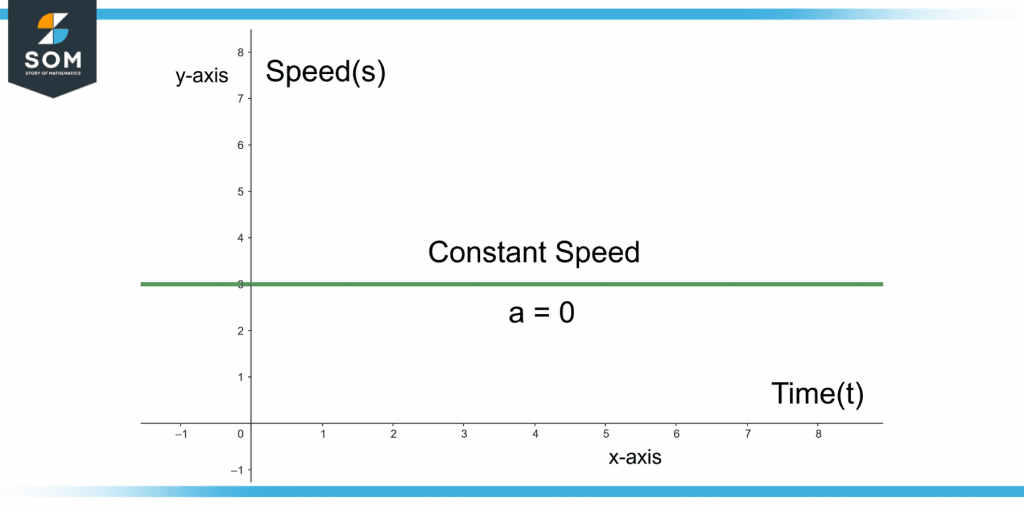
Figure 4 – Speed-Time Graph For Zero Acceleration
The graph shows a straight horizontal line, so the acceleration is zero.
Case 2
If an object moves with a uniform speed, the object accelerates with uniform acceleration.
Figure 5 shows the graph for uniform change in speed in equal time intervals.
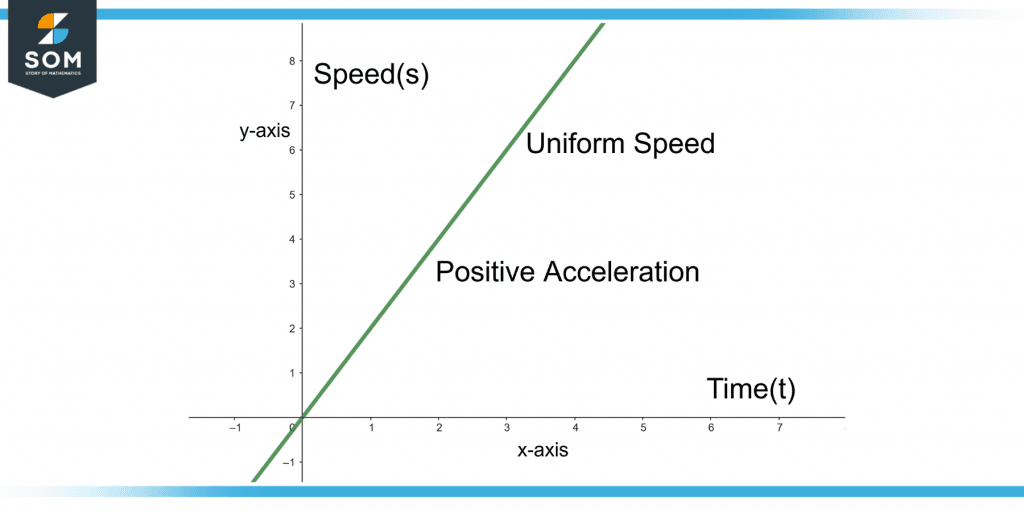
Figure 5 – Speed-Time Graph For Zero Acceleration
The rising slope shows that a positive acceleration is produced.
Speed of Light
The speed of light denoted by c is a universal constant and has an essential role in physics.
It is defined as the speed of light waves when traveling through space or a vacuum. Its value is 299,792,458 m/s or approximately 300,000 km/s.
Solved Example of Speed Calculation
A car covers a 150 km distance in 5 hours. At what speed is the car moving? Also, find the speed in meters per second.
Solution
The distance “d” value is 150 km, and the time “t” given is 5 hours. The formula for speed is given:
s = d/t
Putting the values in the above equation gives:
s = 150 km / 5 h
s = 30 km/h
So, the speed of the truck is 30 km/h. To convert it into meters per second, divide by 3600 and multiply by 1000 as follows:
s = 30(1000)/3600 m/s
s = 8.33 m/s
The speed of the truck in meters per second is 8.33 m/s.
All the images are created using GeoGebra.
