Square Centimeter|Definition & Meaning

Measurements consisting of two lengths are known as square areas. There are two lengths, such as the length of a square centimeter, and then multiply those two lengths together to give a unit of area.

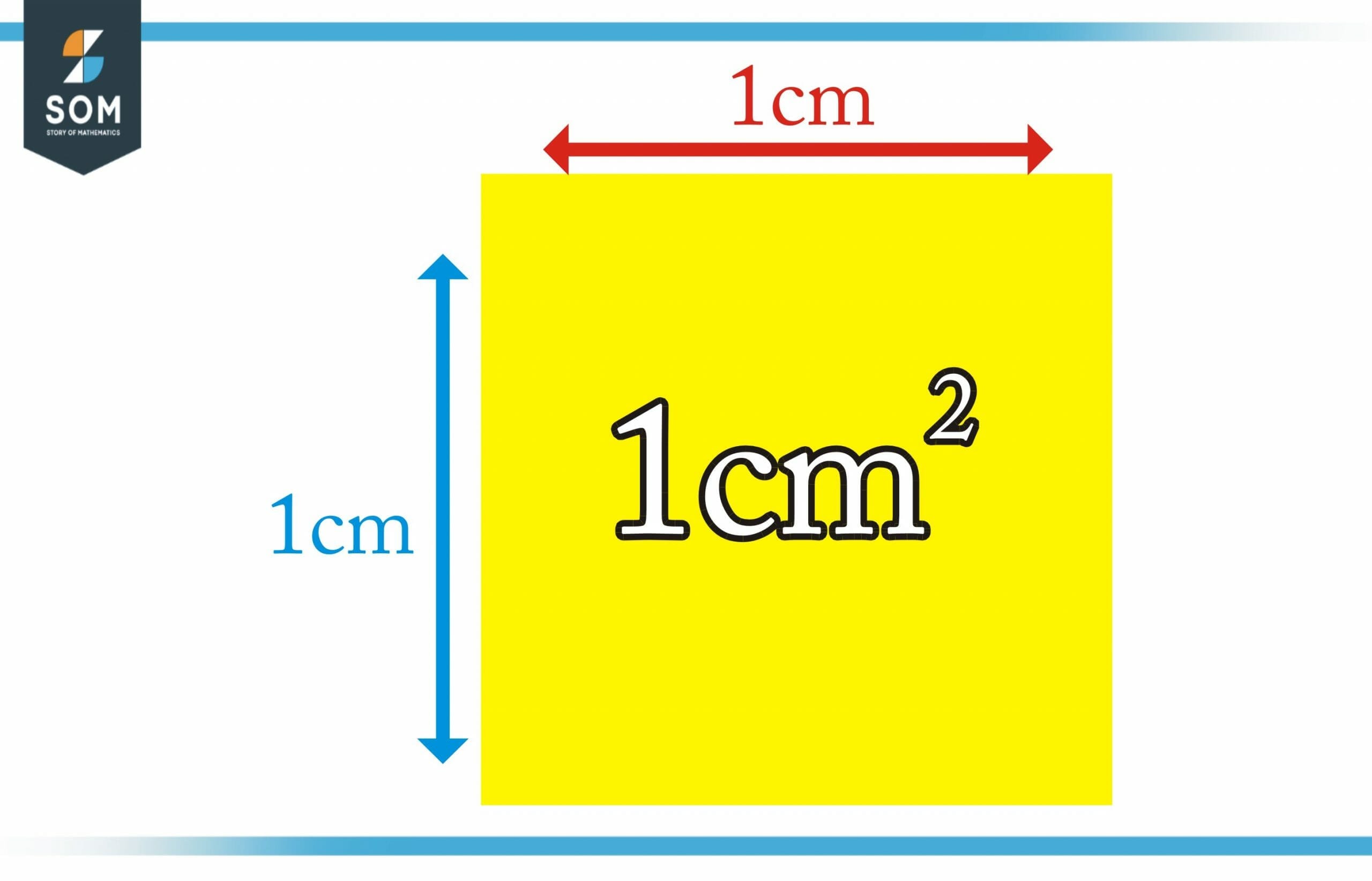
Figure 1 – Representation of 1 square centimeter

A square centimeter is a unit of measurement that measures each length in centimeters, so if we multiply centimeters by centimeters, we end up with a square centimeter. Any area can be calculated as the area made up of several unit squares without the area having to be in the shape of a square. 

Any area can also be estimated from the area made up of some number of squares made up of. It can be shown as an example that a rectangle of 3 cm with 2 cm sides is made up of 6 squares with 1 cm2 area each. As a result, 6 cm2 is the rectangle’s area.

A Measurement System

In the International System of Units (SI), one of the most widely used systems of measurement, a square centimeter represents a unit of area. From square meters, the SI unit of area, square centimeters are derived. With SI, you can convert an area measurement, such as square meters, into a bigger or smaller measurement.

SI is a system that uses prefixes to denote a particular power of 10 concerning the base unit, such as meter in this case, by which we modify it. When the “centi-” prefix is used, it indicates that it indicates 10^-2, so if you want to express a square area such as 2m² in cm², multiply it by (2²)2, which is 20,000cm².

In other words, because one meter is equal to 100 centimeters, (100 cm²)2 is equal to 10,000 cm².

For those living in the US, where US customary units are frequently used, it can also be useful to have a basic understanding of how to convert between different measurements of the area.

Square Centimeters and How To Measure Them

Using square centimeters to measure the area of an object or shape requires two steps. To calculate the area of a shape in square centimeters, you measure parts of the shape and then use the appropriate equation.

Measurement and calculation of objects differ depending on their shape. Measuring square centimeters requires using metric rulers or tape measures since a centimeter is a metric unit of measurement.

1. Measure with a centimeter-based measuring device. The 30 cm ruler is ideal for measuring the area of small shapes or objects. Make use of a metric measuring tape or meter stick when measuring large objects or rooms.
2. Use a metric ruler to measure the shape’s length, height, width, or diameter. You should place the number “0” at the edge of one side of the shape and note the number at the edge of the other side of the shape. In the case of the number “10,” you have measured the part of the shape that is 10 centimeters long.
3. To measure triangles and other shapes, use a protractor. The protractor bottom should be lined up with a triangle base to measure triangle height. Make a mark on the base where the protractor’s vortex sits with the 90-degree mark of the protractor placed at the corner of the triangle perpendicular to the base. The height is measured with a ruler between the triangle’s corner and the vortex mark.
4. For more accurate measurements, use millimeters and centimeters. The number of small millimeter marks between each 13 and 14 cm mark on the ruler will give you an idea of how many millimeter marks you should count between each 13 and 14 cm mark on the ruler if your part of the shape is slightly longer than 13 cm. It is 13.5 cm, or 13 cm and 5 mm if you count the five marks.

Figure 2 – Conversion of square centimeter in different units

Areas of Different Polygons

Rectangles

Using the rectangle’s length and width in centimeters, find its area in square centimeters. By multiplying the length by the width, you can get the area of the rectangle. For example, consider a rectangle having a 5 cm length and 3 cm width. The area of the rectangle will be 15 cm².

Triangles

Measure the base and height of a triangle to find the area in square centimeters. Multiply the height and base of the triangle and divide them by two to get the area of the triangle. In the case of a triangle with a size of 5 cm by 2 cm, the equation goes as follows (5 cm x 2 cm)/2 = 5 cm². In mathematics, the triangle has an area = base × altitude / 2.

Squares

Measure all the sides of the shape to ensure it is a square. The shape is a square, not a rectangle, if all the sides are the same length. Take one of the square’s sides and measure it. The length should be multiplied by itself.

If you have a length of 5 cm, for example, you would multiply 5 cm by 5 cm. The area of the square, in this case, is 25 cm². In mathematics, a square has an Area=Side².

Solved Mathematical Examples

Example 1

What will be the area of the rectangle when it is 3 cm in length and 7 in cm width?

Solution

As we know that:

A = length × width

A = 3 cm × 7 cm = 21 cm²

Example 2

If one of the sides of the square is 7 cm, find the area of the square.

Solution

As we know that:

A = side²

A = (7 cm)²

Area of square = 49 cm²

Example 3

How much area does a triangle with an altitude of 8 cm and a base of 4 cm have?

Solution

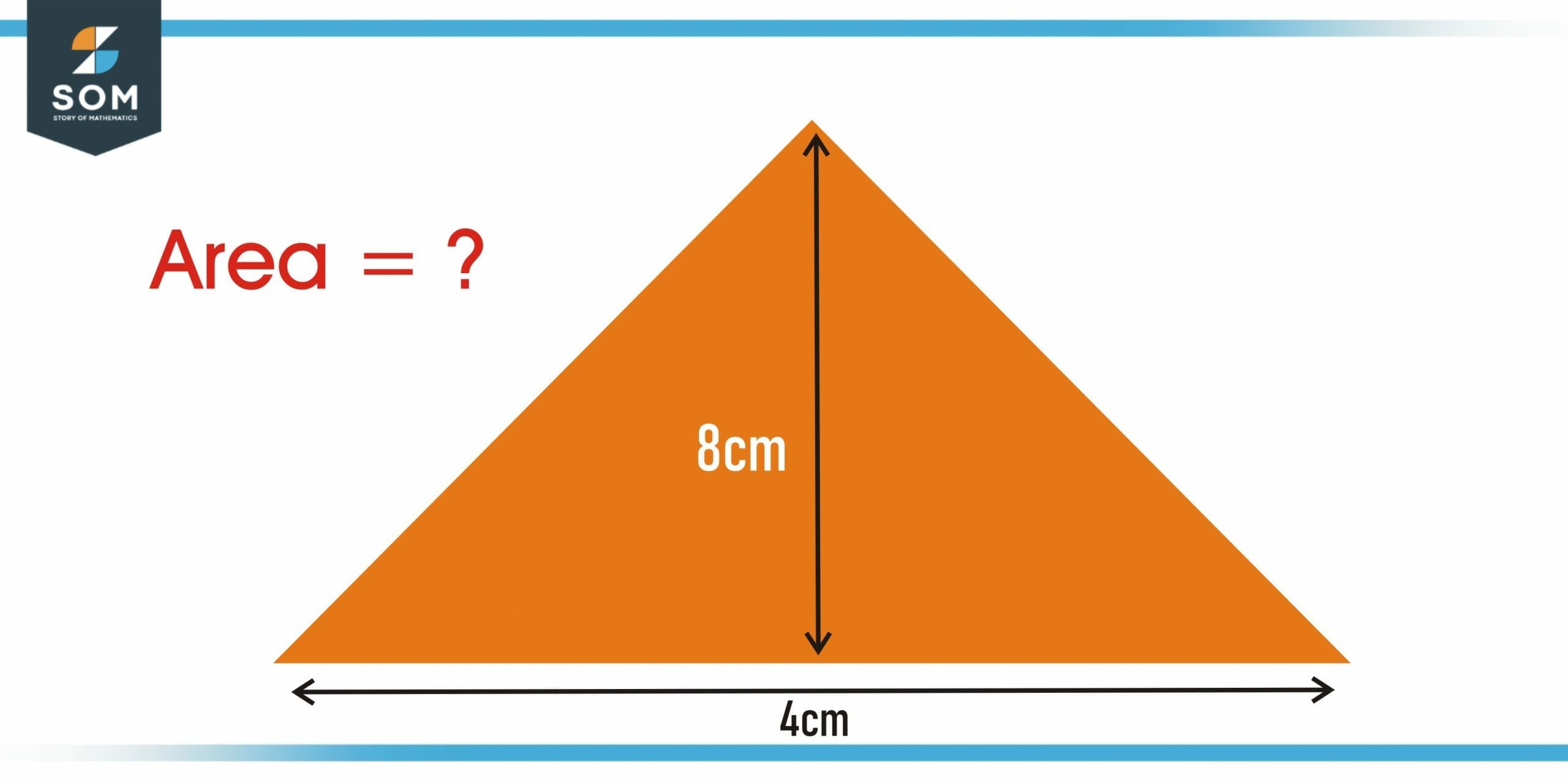
Figure 3 – A triangle with a given altitude and base

As we know that:

A = base × altitude/2

A = 8 cm × 4 cm / 2

Area of triangle = 16 cm²

All the mathematical images are generated using GeoGebra.

Square Definition < Glossary Index > Square Kilometer Definition