Square|Definition & Meaning

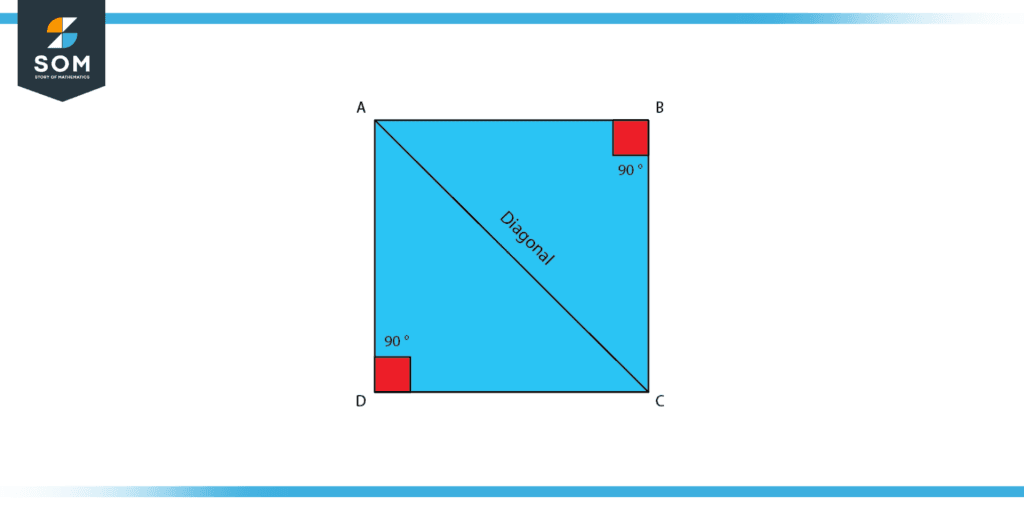
Figure 1: A square ABCD

A square is also equivalent to a rectangle having equal length and width. Many objects can be found in your surroundings that have a square shape. The checkerboard, art sheets, bread slice, picture frame, pizza box, wall clock, etc., are typical instances of this shape. 

A polygon is a shape in geometry that has at least three inner angles or straight edges surrounding it. They have no curves and are closed shapes constructed of straight lines.

The most prevalent polygons are:

• Triangle (3-sided polygon)
• Quadrilateral (4-sided polygon)
• Pentagon (5-sided polygon)
• Hexagon (6-sided polygon)
• septagon (7-sided polygon)
• Octagon (8-sided polygon) and so forth

A polygon is a closed, two-dimensional form with any number of straight sides. To put it simply, a square is a polygon with four sides.

Square Shape

A square is a four-sided polygon with sides that are all the same length and angles that are all exactly 90 degrees. The square has a form that makes both sides symmetrical if it is divided down the middle by a plane. The opposite sides of a square are equal on either half, giving the shape of a rectangle.

Difference Between Square and Rectangle

The main distinction between a square and a rectangle is that the former square has equal lengths on each of its sides, but the latter has equal lengths on each of its opposite sides.

• A square has an equal length on either side. In the case of a rectangle, only the diagonal sides are equal in length.
• A square’s diagonals are each other’s perpendicular bisectors. A rectangle’s diagonals are not the perpendicular bisector of one another.
• The area of a square is obtained by multiplying either of the sides (a x a), while the area of a rectangle is the product of the length and width of its sides (l x w).
• A square’s perimeter equals 4 x. (length of a side), while a rectangle’s perimeter is equal to 2 (length + width).

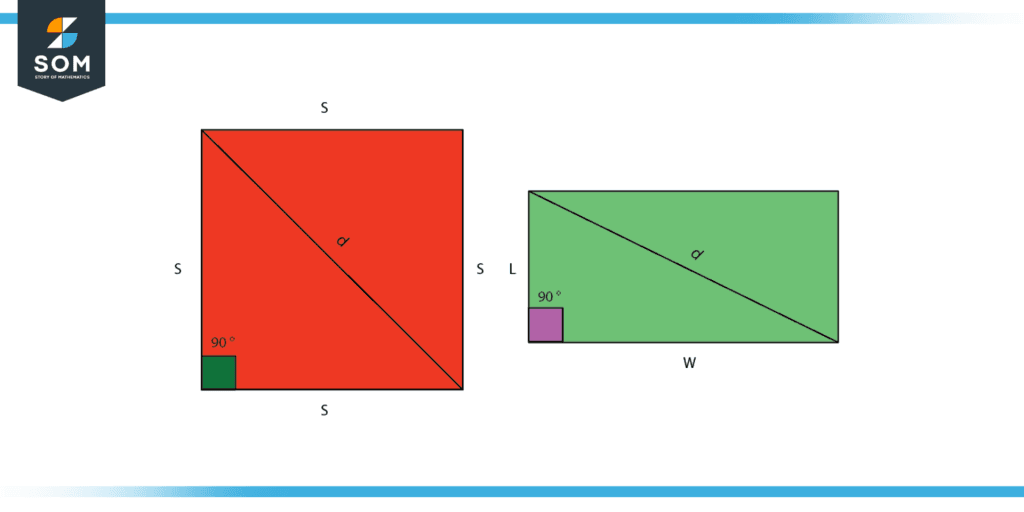
Figure 2: Difference between square and rectangle

Properties of a Square

The following is a list of a square’s most key properties:

• The measure of each of the interior angles is 90°.
• 360° is the result of adding together all interior angles.
• The square’s opposite sides are parallel to one another, and its four sides are congruent or equal to one another.
• The square’s diagonals form a 90° angle with one another.
• The square’s two diagonals are equal to one another.
• The square has four sides and four vertices.
• The square is divided into two identical isosceles triangles by its diagonal.
• The square’s sides are shorter than its diagonals in length.
• Its two diagonals form a straight angle with one another.

Square Formulas

We are aware that a square is a figure with four equal sides. In geometry, there are three fundamental square formulas that are frequently employed. The first one involves computing its area, the second one involves determining its perimeter, and the third one involves calculating the diagonal of a square formula. Let’s take a closer look at these square formulas. 

Area of a Square

The space a square takes up is its area. Chess boards, square wall clocks, and other similar objects are some instances of square shapes. To determine the area that these objects occupy, we can utilize the square’s area formula. The area of a square is calculated by multiplying either of its sides with each other or simply taking the square of its side’s length. 

Area of square = a$^2$

where a is the side of the square, is how the area of a square is calculated. Square units such as square centimeters, square meters, and so on are used to express it.

Perimeter of a Square

The complete length of a boundary of a square is its perimeter. So, by summing the lengths of all the sides, it is possible to determine the square’s perimeter. Because a square has four sides, its perimeter may be determined by adding all four of its sides.

To determine the measurement of a square’s boundary, we can utilize the square’s perimeter formula. A square’s perimeter can be found by adding the lengths of all four sides. Therefore, the square’s perimeter equals:

Perimeter of square = s + s + s + s = 4s

Linear units like cm, m, inches, and so forth are used to express it.

Diagonal of a Square

A line segment connecting any two of a square’s non-adjacent vertices is known as the diagonal of a square. The diagonals of the square in the next figure are AC and BD. The lengths of the lines AC and BD are identical, as you can see. A diagonal divides a square generating two equal right triangles, each of which has a diagonal that serves as the hypotenuse.

Let’s examine the method used to calculate the square’s diagonal formula. 

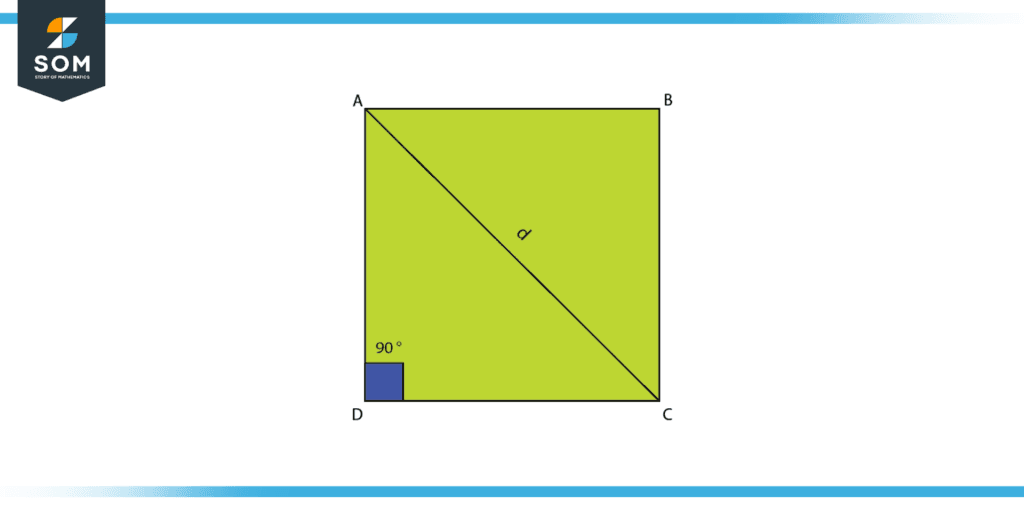
Figure 3: Calculating the formula for the diagonal of a square

Let “a” denote the side length, and “d” denotes the diagonal length of a square, using the example square above as an example. For the triangle, we can apply the Pythagoras theorem.

ADC = d$^2$ = a$^2$ + a$^2$

Square roots on both sides result in the following:

\[ \sqrt{d^2} = \sqrt{2a^2} \]

Consequently, the formula for the diagonal of a square is:

Diagonal of a square (d) = $\sqrt{2}$ × a

Examples Using the Formulas of Square

Example 1

What are the lengths of the sides of a square whose area is 25 square cm?

Solution

The square has an area of 25 sq. cm provided in the question.

As we are aware that taking the square of the length of its side gives us the area of a square, therefore: 

Area of square = a$^2$

As a result, when we substitute the area value, we get the following:

25 = a$^2$

a = $\sqrt{25}$ = $\sqrt{(5)(5)}$

= 5 cm

As a result, the square’s side length is 5 cm.

Example 2

Determine the diagonal of a square with a side of 7 cm using the square’s key characteristics.

Solution

As we know,  the diagonal of a square can be computed using the formula:

d = $\sqrt{2}$ × a

Where “a” represents the side length. Plugging in the value of the length of the side, we get:

d = $\sqrt{2}$ × a

= $\sqrt{2}$ × 7

= 9.89 cm

Thus, the measure of the diagonal of a square having a 7 cm side length is 9.89 cm.

All images/mathematical drawings were created by GeoGebra.

Sphere Definition < Glossary Index > Square Centimeter Definition