JUMP TO TOPIC
Square Measure|Definition & Meaning
Definition
Any unit that measures area is called a square measure. Therefore, all squared units of length (e.g., squared meters or m$^2$, squared centimeters or cm$^2$) and some special units like hectares (ha = 100 m x 100 m = 10,000 square meters) and acres (ac = 0.4047 hectares) are called square measures.
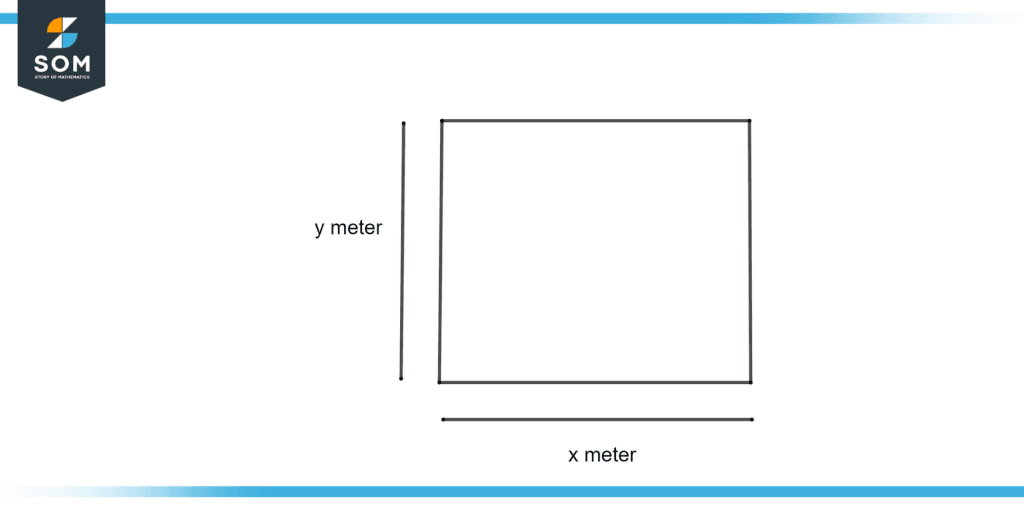
Figure 1 – Square Measure
Figure 1 illustrates the graphical representation of square measure in which we have a square of x meter by y meter. The area of this square is x * y m2.
The International System of Units (SI) uses the square meter (international notation used by the International Bureau of Weights and Measures) or the square meter (American notation) as the unit of area, with the symbol m2 . The area of a square with a side of 1 meter.
The size of the spot on the surface is determined by its area. Surface area refers to the open surface or edge area of a three-dimensional object, and planar area or planar area area refers to the area of the shape or planar layer.
Area can be interpreted as the quantity of material with a specific thickness required to create a model of the shape or as the quantity of paint required to cover a surface in a single coat completely. It is the two-dimensional equivalent of the volume of a solid or the length of a curve, both of which are one-dimensional concepts (a three-dimensional concept).
By comparing a form to squares of known size, one may determine the area of a given shape. The standard unit of area in the International System of Units is the square metre, which is the size of a square whose sides are one metre long (SI).
A shape having an area of 3 square metres would be the same size as three of these squares. All other shapes or surfaces’ areas are dimensionless real values, and the area of a unit square is one according to mathematics.
The areas of basic forms like triangles, rectangles, and circles may be calculated using a number of well-known formulae. By splitting any polygon into triangles, one may use these formulae to get the area of the polygon.
Typically, calculus is required to determine the area of structures having curved borders. In reality, the problem of measuring the area of flat figures served as one of the primary impetuses for the historical development of calculus.
In modern mathematics, area plays a vital role. In addition to the area’s apparent importance in geometry and calculus, it also serves as a crucial aspect of surfaces in differential geometry and is related to the definition of determinants in linear algebra.
Lebesgue measure is used in analysis to specify a subset of the plane’s area, albeit not all subsets are measurable. Area is frequently considered a particular instance of volume for two-dimensional regions in higher mathematics.
When SI prefixes are added and removed, multiples and sub-multiples are produced; however, when the unit is exponential, the amounts increase exponentially by the appropriate power of 10.
For instance, 1 kilometer is 103 (one thousand) times longer than 1 meter, but 1 square kilometer has an area that is (103)2 (106, one million) times larger, and 1 cubic kilometer has an interior volume that is (103)3 (109, one billion) cubic meters.
A square or rectangle’s area is measured in square meters. It may also be used to calculate the size of a circle, even though the SI unit for doing so is the square kilometer. Measuring the size of a room in a home or apartment is one example of how to utilize the square meter in practice. A piece of land’s area may also be determined using it.
Calculation of Square Meter
You need to know the square or rectangle’s length and breadth in order to calculate square meters. The region of the shape is another name for this. Length times width equals m2 is the formula for determining square meters. For instance, if your square is 3 meters long and 2 meters wide, then 3 x 2 Equals 6 m2.
It’s critical to understand that area is proportional to the square of the linear dimension when computing area. As a result, the area increases by four times if all linear dimensions are doubled and by one-fourth if all the linear dimensions are reduced by half.
10,000 centimeters squared (104 cm2) or 1,000,000 millimeters squared (106 mm2) are equivalent to one square metre. In the opposite context, 1 m2 is equivalent to 0.000001 km2 .
Conversion of Square Meter into Other Units
Multiply 1,550 to convert square meters to square inches. Divide by 1,000,000 to convert square meters to square kilometers. Multiply 10.763910417 to convert square meters to square feet. Divide square meters by 2,589,988.1103 to get square miles.
Difference Between Square Meter and Meter Square
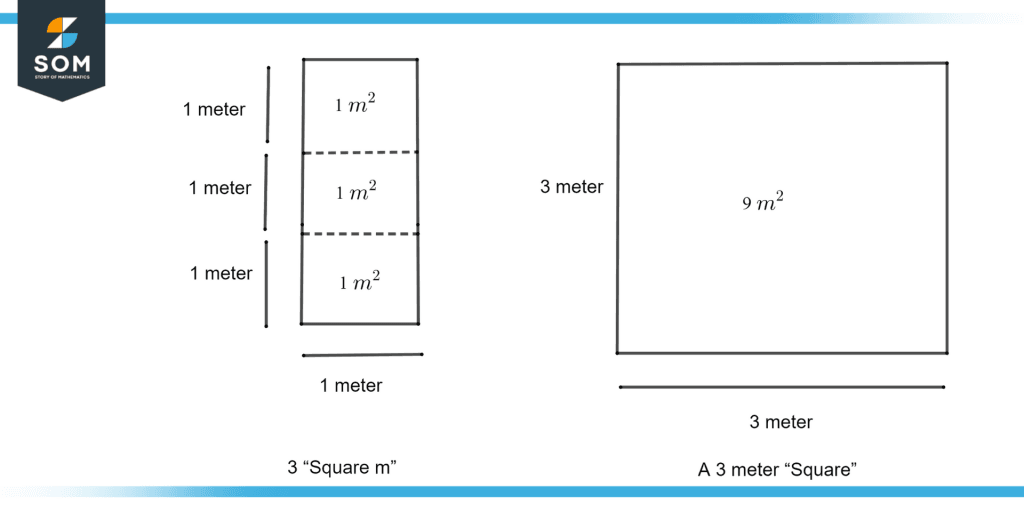
Figure 2 – Square Meter and Meter Square
Figure 2 illustrates the difference between the square meter and the meter square. 3 “Square meter ” means three squares, each square of 1 meter by 1 meter, and 3 meters “square” means a square of 3 meters by 3 meters which is equal to 9 square meters.
Square units in metric measurements include square meters and square millimeters, whereas square units in customary units include square inches and square feet.
Geometric Area Formula
In order to measure the area of any geometric shape, we have different formulas. Some of these formulas are illustrated below:
Area of a square = length2
Area of a triangle = $\dfrac{1}{2} $ base height
Area of a circle = $\pi$ r2
Area of a rectangle = base $\times$ height
Some Examples of Square Measure
Example 1
Find the area of the triangle illustrated in figure 3.
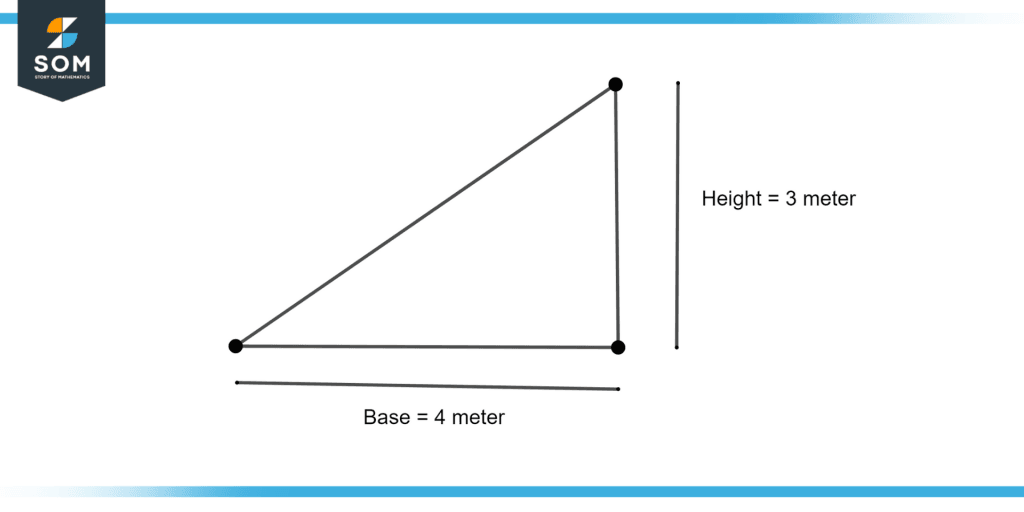
Figure 3 – Area of a triangle
Solution
Area of a triangle = $\dfrac{1}{2}$ $\times$ base $\times$ height
Area of a triangle = $\dfrac{1}{2}$ $\times$ 4 m $\times$ 3 m
Area of a triangle = $\dfrac{1}{2}$ $\times$ 12 m
Area of a triangle = 6 m2
The area of the triangle is equal to 6 square meter.
Example 2
a) Find the area of a rectangle with a base of 6 meters and a height of 5 meters.
b) Find the area of the circle if the diameter of the circle is ten meter.
Solution
a) The formula for calculating the area of the rectangle is:
Area of a rectangle = base $\times$ height
Area of a rectangle = 6 meter $\times$ 5 meter
Area of a rectangle = 30 m2
b) The formula for calculating the area of the circle is:
Area of a circle = $\pi$ r2
We need to calculate the radius of the circle from the given diameter, so we will divide ten by two. Then, we have a radius that is equal to five:
Area of a circle = 3.142 $\times$ 5 $\times$ 5
Area of a circle = 78.55 square meters
All images were created using GeoGebra.
