Square Meter|Definition & Meaning

Why Do We Use a Square Meter?

A Square meter is a unit given by the International System of Units (SI) to find the area of a square. It is also known as meter squared, which is represented by m² or can be abbreviated as sq m. 

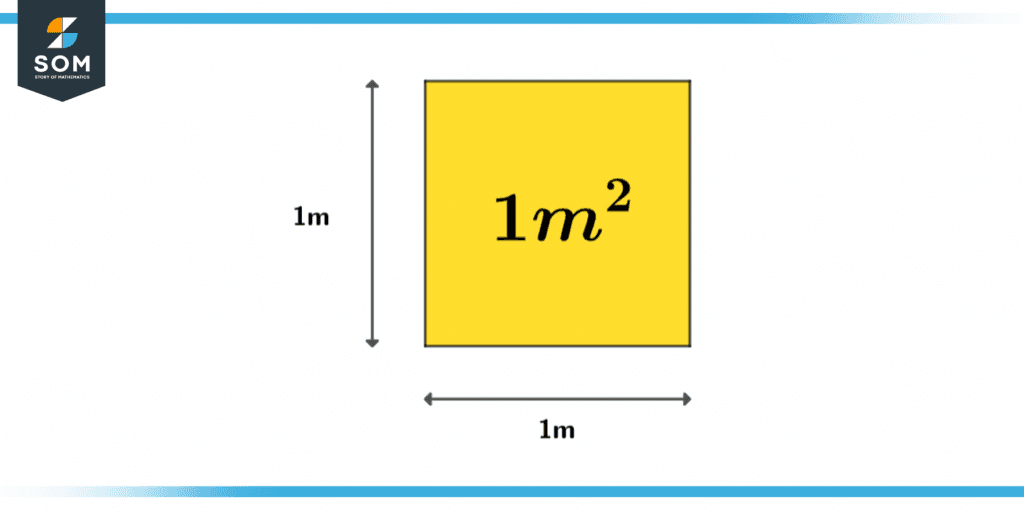
Figure 1 – A Square Meter

We use a square meter to measure the area of a square or a rectangle. It can also be used to find the area of a circle since it has equal sides and can be used as a standard. In the practical application, we use a square meter to find the area of a room or a piece of land.

Calculation and Conversion of Square Meter

A square meter is a unit that we use to measure the area of any object or space, preferably a square or a rectangle. In other words, we use a square meter to measure the area of a given shape. To calculate square meters, we use the following formula:

Length * Width = m²

Let us take an example if there is a square block with a length of 5 meters and width of 4 meters, then we can write it as:

5 * 4 = 20 m²

Another concept that we need to keep in mind is that when we are calculating the area of any shape, its linear dimension must be taken into account since the area is directly proportional to the square of the linear dimension. This means that the value doubles for linear dimensions.

We know that:

1 m² = 10,000 cm or 1000000 mm

Which can also be written in kilometers as:

1 m² = 0.000001 km

This tells us that we can convert square kilometers into different units. Let us look at some of these conversions.

Square Inches

If we want to convert square meters into square inches, we will multiply the given number by 1,550 to get the desired results.

Square Kilometers

If we want to convert a number that is in square meters to square kilometers, then we will divide the number by 1,000,000 to get the result.

Square Feet

If the number that we want to convert is in square meters, so we will multiply by 10.763910417 to get the square feet value.

Square Miles

If we want to convert a number in square meters to square miles, then we must divide the number by 2,589,988.1103 to get the results.

Calculating the Area of Odd-shaped Objects

We can use a square meter to find odd-shaped spaces or objects too. We do this by dividing the space or object into smaller squares or rectangles. This allows us to find the area of those small squares and add them up altogether. For example, look at the following example:

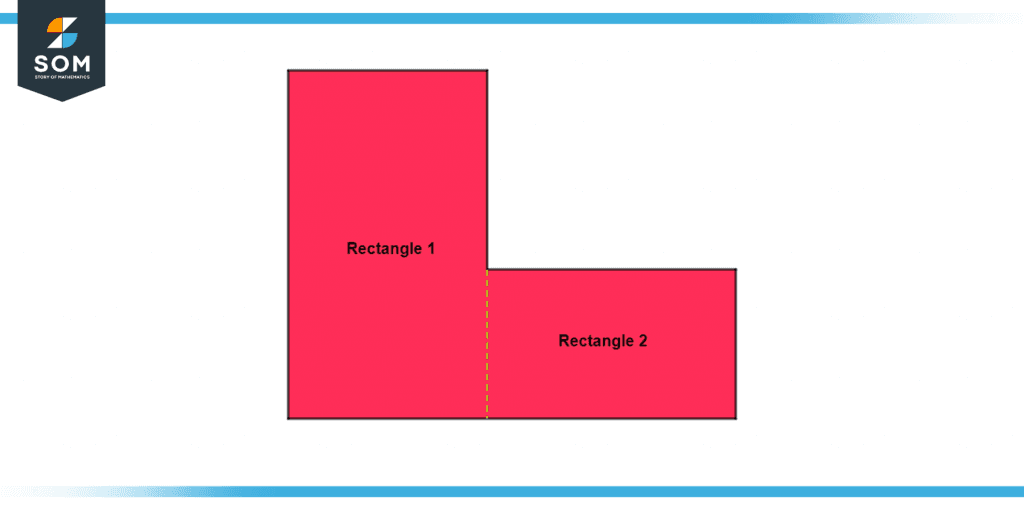
Figure 2 – An odd Shape being Divided into Small Rectangles

In this example, a room is in the L shape. To find the area, we are going to divide it into 2 rectangles and separately find their areas using the formula:

Length * Width = m²

After this, we will add both of the areas together to get the total area of the room, which is desired. Similarly, we can find the area of many other odd shapes.

Practical Applications

Some of the practical applications of the square meter in real life are given below:

• A square meter is used in real estate to find the area of land to price it accordingly. 
• Architects use it to make houses and to calculate the total material that is required. 
• Engineers use it in various fields and can use it in different technology to check the energy required for heating or cooling a space.
• It is used to find the area and other dimensional distances of a piece of land. 
• It is used to find the total energy that a solar panel can produce.
• In geometry, we use it to find the area of different shapes like squares, rectangles, parallelograms, and even a circle.

Solved Examples Involving Square Meters

Example 1

Jane’s room is A meter long, B meters broad, and the height of the room is C meters; She wants to renovate her room, so help her find how many square meters of carpet she will need for her floor and how many square meters of wallpaper she will need for her walls.

Solution

Length of Jane’s room = A

Width of Jane’s room = B

Using the formula:

Length * Width = m²

Now putting values:

A * B = m²

Now for the walls using the formula:

2h(l + b)

Now putting the values:

2C(A + B)

2CA + 2CB 

Example 2

Solve the Following:

1. A square banner has 5 cm as the length of each side. What is the total area in a square meter?
2. A square-shaped banner is being designed to display in the school corridor. Let each side of the square banner be 20m, then what will be the total area of the banner?

Solution

Part 1

As we know that:

Length of each side of the square = a = 5 cm

Area of the square = a²= 5 cm²

But we know that 1 m = 100 cm or 1 cm = 10^-2 m, so:

Area of square = (5 cm)²

Area of square = 25 cm² = 25(10^-2 m)² = 0.25 m²

Part 2

As we know:

Length of each side = 20 m

According to the formula:

Area of a square = side × side

Area of a square = 20 m × 20 m

Hence:

Area of a square= 400 sq.m

Example 3

Petra wants to convert 225 square meters in hectares. Help her out.

Solution

As we know:

1 square meter = 0.0001 hectares

So 225 square meters = 225 × 0.0001 hectares:

225 m² = 0.0225 hectares

So the value of 225 square meters, when converted into hectares, is 0.0225 hectares. 

Example 4

Show and explain how to find the area of a circle using a square meter.

Solution

To find the area of a circle, we will keep in mind the formula:

Area of a circle = πr²

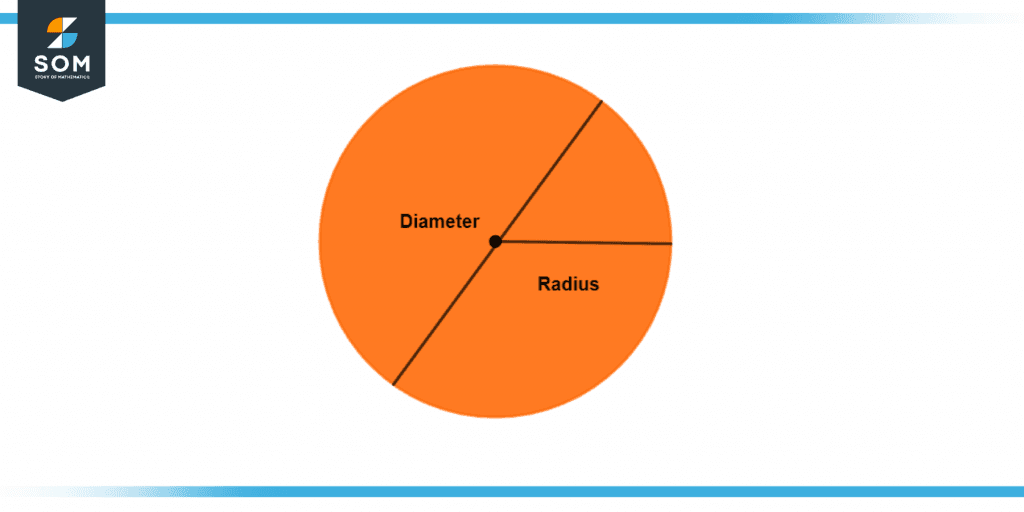
Figure 3 – Area of a Circle

Here r is the radius which, when multiplied by π, gives us the area of the circle, but when we have to use square meters, we divide the circle into triangles and semicircles and further into small squares to find the area.

Images/mathematical drawings are created with GeoGebra.

Square Measure Definition < Glossary Index > Square Number Definition