Square Number | Definition & Meaning

A square number, commonly referred to as a perfect square, is a sum that may be written as the result of multiplying one integer by that number. For instance, the number 4 is a square because 2 × 2 can be used to represent it. Other examples of square numbers include 9 (3 x 3) and 16 (4 x 4).

The square of a number is often denoted using a superscript, such as 25, for the square of 5 (5²). The process of finding the square of a number is also known as squaring the number. The depiction of the concept of square number has been provided in Figure 1 below:

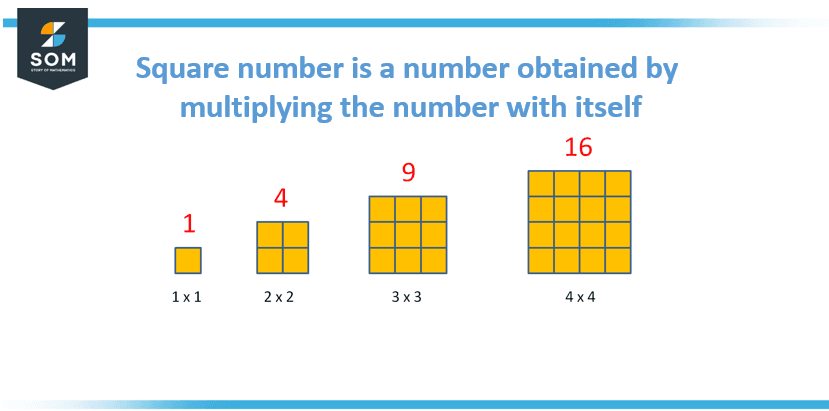
Figure 1: Concept of square numbers

The Mathematical Background of Square Number

In mathematics, the concept of a square number is closely related to the idea of exponentiation with a base of 2. Specifically, a square number can be defined as the result of raising a number to the power of 2. 

Square numbers also have certain properties that are unique to them. For example, the sum of the squares of the integers from 1 to n is given by the formula n(n+1)(2n+1)/6.

The difference between adjacent squares is also equivalent to the total digits from the lower number to the following adjacent square. For example, the difference between the squares of 4 and 5 is equal to 4 + 5 = 9.

Square numbers also play an important role in many areas of mathematics, including number theory, algebra, and geometry. For example, A square is a two-dimensional geometric object with equal sides and right angles on all four sides. The equation side x side gives the area of a square of the length of one side.

Properties of Square Number

Square numbers have several properties that make them unique and useful in mathematics. Some of these properties include:

1. The formula gives the sum of the squared values of the integers between 1 to n. n(n+1)(2n+1)/6.
2. The difference between consecutive squares is equal to the sum of the integers from the lower number to the next consecutive one. For example, the difference between the squares of 4 and 5 is equal to 4 + 5 = 9.
3. An expression for a square number is the sum of an odd number of consecutive values beginning with 1. For example, 4 is the sum of 1 + 2 + 1.
4. All square numbers are positive integers, and all positive integers have at least one square factor, which makes them a subset of positive integers.
5. A positive integer is the square root of a square number. For instance, 4 is the square root of 16.
6. The squares of consecutive integers are consecutive odd numbers.
7. An even number’s square is always even, whereas an odd number’s square must be odd.
8. A negative number’s square has always been positive.

Square numbers for counting numbers 1-12 are depicted in Figure 2 below:

Figure 2: Square numbers for numbers 1-12

Lagrange’s Four-Square Theorem

Lagrange’s four-square theorem, also known as Lagrange’s four-square identity, states that every positive integer can be represented as the sum of, at most, four square numbers.

The theorem is named after Joseph-Louis Lagrange, a French mathematician who first proposed it in 1770. The mathematical formula for Lagrange’s four-square theorem can be stated as follows:

Let n be a positive integer. Then, there exist non-negative integers w, x, y, and z such that:

n = w² + x² + y² + z²

This means that any positive integer n can be represented as the sum of at most four square numbers. For example, consider the number 12. According to Lagrange’s four-square theorem, it can be represented as the sum of, at most, four square numbers:

12 = 0² + 2² + 2² + 2²

Another example is the number 20, which can be represented as the sum of at most four square numbers:

20 = 4² + 2² + 0² + 0²

It’s important to note that Lagrange’s four-square theorem doesn’t always guarantee that a representation of four squares is possible for any given integer; in some cases, it can be represented with less than four squares.

The elaboration of computing square numbers using Lagrange’s four-square theorem has been given in Figure 3 below:

Figure 3: Computing square numbers using Lagrange’s Four-Square Theorem

Lagrange’s four-square theorem is a fundamental result in number theory and has many important implications in mathematics and cryptography. It has been used to prove other important theorems, such as Fermat’s Last Theorem for the case n = 4, and it is also used in the study of Diophantine equations.

Odd and Even Square Numbers

Odd and even square numbers refer to the property of a square number being either odd or even.

Any integer that cannot be divided by two is considered odd, meaning it leaves a remainder of 1 when divided by 2. For example, the numbers 1, 3, 5, and 7 are all odd numbers. Any number that is divisible by two is said to be even, meaning it leaves no remainder when divided by 2. For instance, even numbers include 2, 4, 6, 8, etc.

When it comes to square numbers, the property of being odd or even is determined by the number being squared. If the number being squared is even, then the resulting square number will also be even. If the number being squared is odd, then the resulting square number will also be odd. For example, the square of the even number 4 is 16, which is also an even number and the square of the odd number 3 is 9, which is also an odd number.

It’s important to note that all square numbers are positive integers, and all positive integers have at least one square factor, which makes them a subset of positive integers. The property of being an odd or even square number is useful in certain mathematical problems, and it can help identify patterns or simplify equations.

Square Number’s Relationship with Triangular Numbers

Square numbers and triangular numbers have a unique relationship, which can be expressed mathematically. A triangular number is one that may be expressed as the accumulation of a series of successive integers, starting with 1.

For example, the triangular number 6 can be represented as 1 + 2 + 3. The n^th triangular number, T_n, can be represented as the formula:

T_n = n(n+1)/2

A square number, on the other hand, is a quantity that may be described as the result of multiplying an integer on its own; for instance, 4 is a square number because it can be expressed as 2 x 2. The nth square number, S_n, can be represented as the formula:

S_n = n²

The relationship between square numbers and triangular numbers can be expressed mathematically by the equation:

S_n = T_n + (n – 1)T_n – 1

In other words, the nth square number is equal to the nth triangular number plus (n-1) times the (n-1)th triangular number.

For example, consider the 6th square number and the 6th triangular number:

S_n = 6² = 36

T_n = 6(6+1)/2 = 21

Plugging these into the equation, we get:

36 = 21 + (6-1)T₅

This holds true, so it confirms the relationship between square numbers and triangular numbers. This relationship between square numbers and triangular numbers is known as the “square pyramidal number theorem.” It’s a simple but important relationship that can be used to solve various mathematical problems, and also some interesting geometric interpretations.

Prime Factorization of Square Numbers

The prime factorization of a square number is the unique way of expressing the number as the product of prime numbers. Every composite number (a number that is not prime) can be expressed as the product of primes, and this is known as the prime factorization of the number.

When it comes to square numbers, their prime factorization can be determined by taking the prime factorization of the number being squared and then squaring each of the prime factors.

For example, consider the square number 16. The number being squared is 4, which has a prime factorization of 2 x 2. Therefore, the prime factorization of 16 is (2×2)² = 2⁴. Another example is the square number 36. The number being squared is 6, which has a prime factorization of 2 x 3. Therefore, the prime factorization of 36 is (2×3)² = 2² x 3².

It’s important to note that the prime factorization of square numbers is different from the prime factorization of the number that is being squared, as the prime factors are squared in the square numbers’ prime factorization.

Knowing the prime factorization of a square number is useful in solving mathematical problems, as well as determining the greatest common divisor or least common multiple of two numbers, and also in comprehending a number’s characteristics.

These properties can be used to identify square numbers, understand patterns in mathematical equations, and solve problems related to square numbers.

Solved Examples

Example 1 – Squaring a Number

Compute the square numbers of 4 and 5.

Solution

The square of 4 (4²) is equal to 4 multiplied by 4, or 16, and the square of 5 (5²) is equal to 5 multiplied by 5, or 25.

Example 2 – Prime Factorization of a Number

Compute the prime factorization of 60.

Solution

The prime factorization of the number 60 is 2 x 2 x 3 x 5.

All images/mathematical drawings were created with GeoGebra.

Square Meter Definition < Glossary Index > Standard Deviation Definition