JUMP TO TOPIC
Surface|Definition & Meaning
Definition
The outer boundary of any three-dimensional object is called the surface. It may be flat as in a pyramid or curved as in a sphere or cylinder. By definition, it is 2D and therefore has no thickness but does have area. The area occupied by the surface is generally called the surface area.
An object’s outermost layer.
- It’s a 2-dimensional boundary that may be flat or curved
- It has an area but still no thickness.
Figure 1 below shows the surface of a cube.
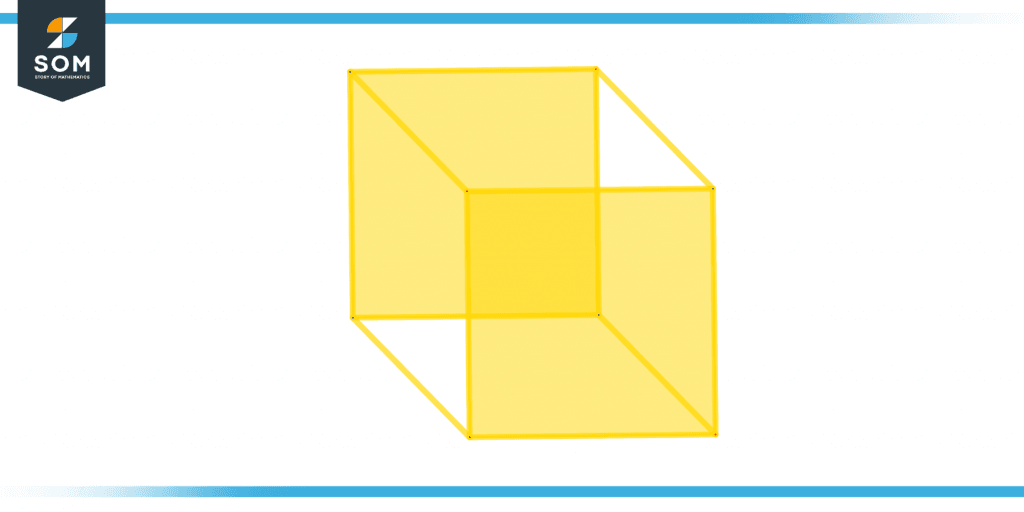
Figure 1 – Surface of a cube.
A 2-dimensional point collection (flat surface), a 3-dimensional point collection with a curve cross-section (curved surface), or the border of any 3-dimensional solid. A surface is a continuous barrier that divides a 3-dimensional space into two sections.
A sphere’s surface, for example, divides the interior from the exterior; a parallel to the horizontal divide the half-plane over it to the half-plane below it. Surfaces are frequently referred to by the name of the area they surround. However, a surface is fundamentally two-dimensional with an area, but the area it encloses has 3-dimensional with a volume.
Types of Surface
There are two types of surfaces
- Flat surface
- Curved surface
Figure 2 below shows the types of surfaces.
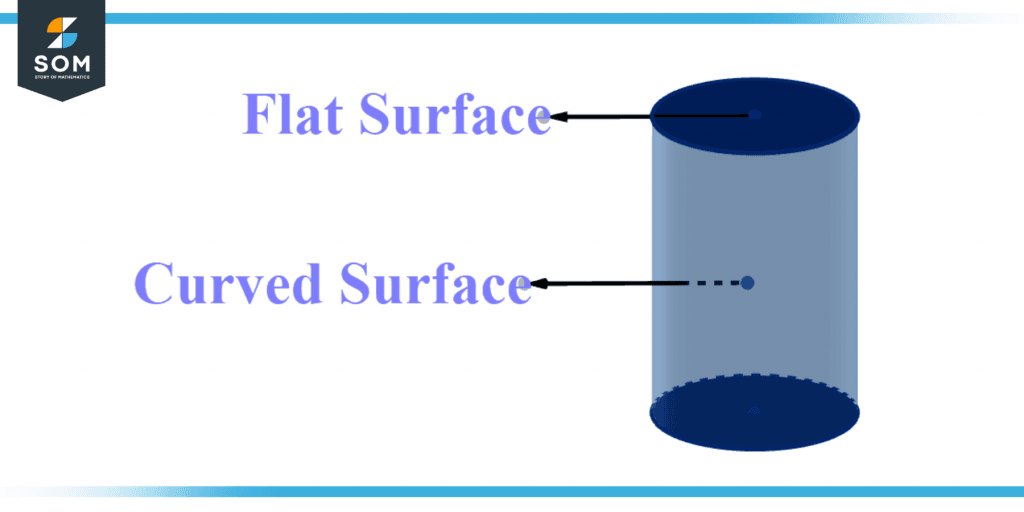
Figure 2 – Types of surfaces in a cylinder.
Flat Surface
The flat surface is another name for a flat surface. Plane geometry is concerned with flat forms that may be drawn on paper, including squares, circles, and triangles. A flat figure or plane has two dimensions: width and length.
A solid, as well as a 3D form, occupies space. The surface of a solid refers to the solid’s outer layer. So when the surface of the solid is a flat surface with really no depths or flatness, it is referred to as a flat surface. Every day, we notice a lot of flat items in our surroundings. For example, a book, desk, or dresser can have a flat surface.
Recognizing Flat Surfaces within 3D Shapes
If we look at various 3D blocks, cubes, pyramids, and prisms, we’ll see that they only have flat or plane surfaces. 3D figures and forms have flat, curved surfaces, such as cylindrical or cones. Furthermore, particular 3D objects, such as spheres, have no flat surfaces and just one curved surface. You can move an object with a flat surface. If an object has a curved surface, you can roll it along it.
The cubes have six sides, each of which is a square. The cylinders have a curved surface plus two flat surfaces that are equal circles. A spherical one has only one curved surface.
Curved Surface
A curved surface is indeed a rounded, non-flat surface. A curved surface can be found everywhere around an item. Such items have a single surface all the way around. Spheres are examples of things with curved surfaces all around.
Real-world examples of items with curved surfaces include balls, globes, eggs, pipes, domes, and so on.
There are 3D forms that solely have flat surfaces. For example, a cube, cuboid, pyramid, and prism are all 3D geometries formed out of flat surfaces. They have squares, rectangles, triangles, and parallelograms as their surfaces. They don’t have any curved surfaces. Boxes, cubes, pyramids, prisms, bricks, and other 3D structures with curved surfaces are not examples.
Area of a Surface
A three-dimensional object’s surface area is the sum of its faces. Real-world applications of surface areas include wrapping, painting, and constructing objects to get the most excellent potential design. An object’s surface area is the total area that all of its surfaces occupy.
There are two groups for the surface area:
- Total surface area
- The surface area that is laterally oriented or curved
Surface Area Types
Three-dimensional forms can have either a total surface area or a curved/lateral surface area. Although the curved and lateral area only comprises the area of either the lateral faces of the forms, the surface area encompasses the space of all of the faces of a shape. To understand the distinction between the total and curved surface area, look at the cylinder shown below.
Figure 3 below shows the area of the cylinder.
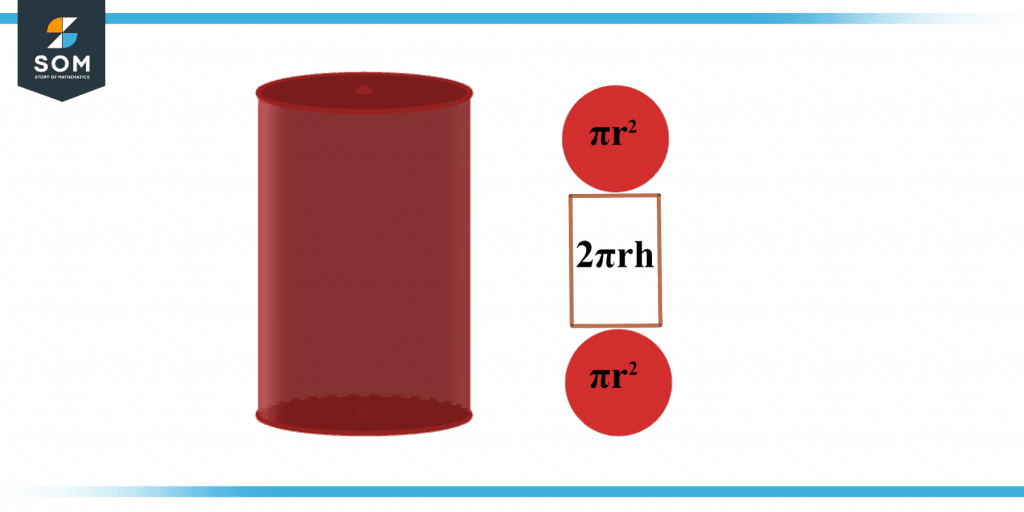
Figure 3 – Surface area of a cylinder.
Prism Surface Area
A prism is a 3D solid object made up of two congruent foundations, a polygon, and two congruent lateral sides, rectangular in shape.
Only a prism has two distinct areas: its lateral total surface area and the total lateral surface. Whereas the lateral surface area total of just a prism is the combination of both the regions of each of its lateral faces, the external overall surface area of a prism is the product of something like the main area and the area among its bases.
The prism’s lateral surface area = height × base perimeter
The prism’s total surface area = Lateral surface area of prism + area of the two bases = Lateral surface area + (2 × Base Area) = (Base perimeter × height) + (2 × Base Area).
Based on how the base of prisms is shaped, there are seven different varieties of prisms. The formulae used to calculate the overall surface area of a prism varies, just as the bases of various prisms do.
Examples of Surface
Some of the examples of surfaces are listed below
Example 1
What is the ice cream cone’s surface area if its radius and slant height are 5 and 8 inches, respectively?
Solution
Given: slant height equals 8 inches, radius = 5 inches.
Cone’s surface area is equal to pi(r + l).
= $\pi$ × 5(5 + 8)
= 3.14 × 5 × 13
= 204.1 square inches
The cone has a surface area of 204.1 inches square.
Example 2
How big is its surface area if a cube has 5 inches on each side?
Solution
Given that the cube’s sides are 5 inches long.
A cube’s surface area equals 6a2.
a =5 inches (given)
When we replace the quantities in the equation, we obtain,
= 6(5)2
= 6 (25)
= 150 square inches
The cube’s 54 inches2 of surface area.
All Images are made using GeoGebra.
