Surd|Definition & Meaning

Surds are a special class of numbers that cannot be expressed as a simple fractional number. As the above definition suggests, one of the easiest ways of defining such numbers is through the n^th root route. The following figure shows some examples of surds that are most elementary in nature. 

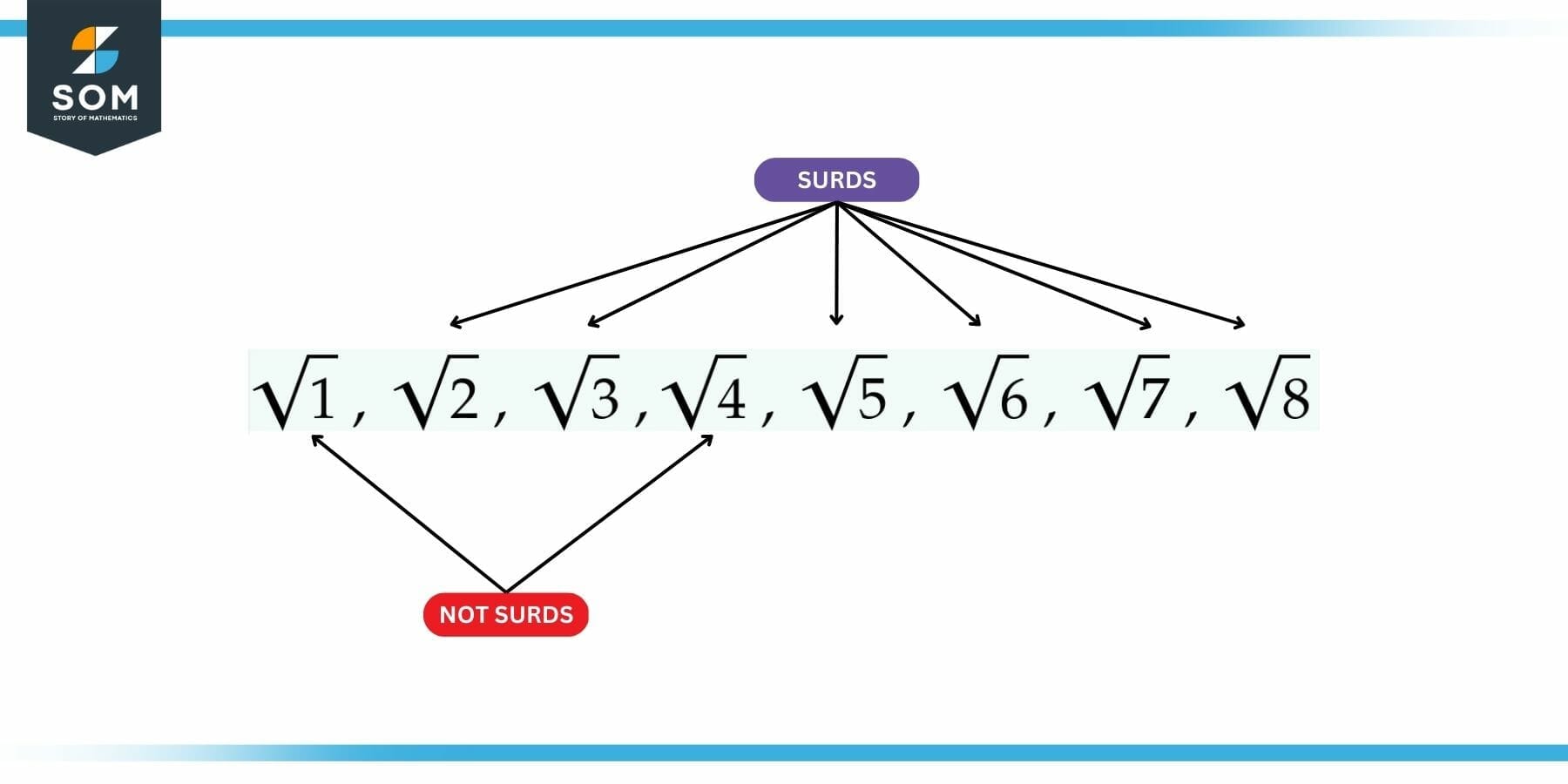
Figure 1: Some Examples of Elementary Surds

Examples of Surds

As per the example given above, we can easily explain surds with the help of some elementary roots. As a litmus test, we will see if the given root can be written without the square root. Let us consider all the above numbers one by one:

 $\sqrt{1}$ = 1 $\to$ Not Surd

 $\sqrt{2}$ $\to$ Surd

 $\sqrt{3}$ $\to$ Surd

 $\sqrt{4}$ = 2 $\to$ Not Surd

 $\sqrt{5}$ $\to$ Surd

 $\sqrt{6}$ = $\sqrt{2}$ x $\sqrt{3}$ $\to$ Surd

 $\sqrt{7}$ $\to$ Surd

 $\sqrt{8}$ = $2\sqrt{2}$ $\to$ Surd

Types of Surds

The different types of surds are as follows:

1. Simple Surds: Surds comprising of a single term are called simple surds. Examples in the figure 1 are all simple surds.
2. Pure Surds: Surds that are completely irrational and can’t be written as a fraction are termed as pure surds.
3. Similar Surds: If two or more surds have a common factor that they are called similar surds.
4. Mixed Surds: If a surd can be represented as a product of a rational and irrational number then it can be called a mixed surd.
5. Compound Surds: If a surd is made up of addition or subtraction of any two or more surds, then its called a compound surd.
6. Binomial Surds: If a surd is constituted by other simpler surds, its called a binomial surd.

The following figure summarizes all these different types:

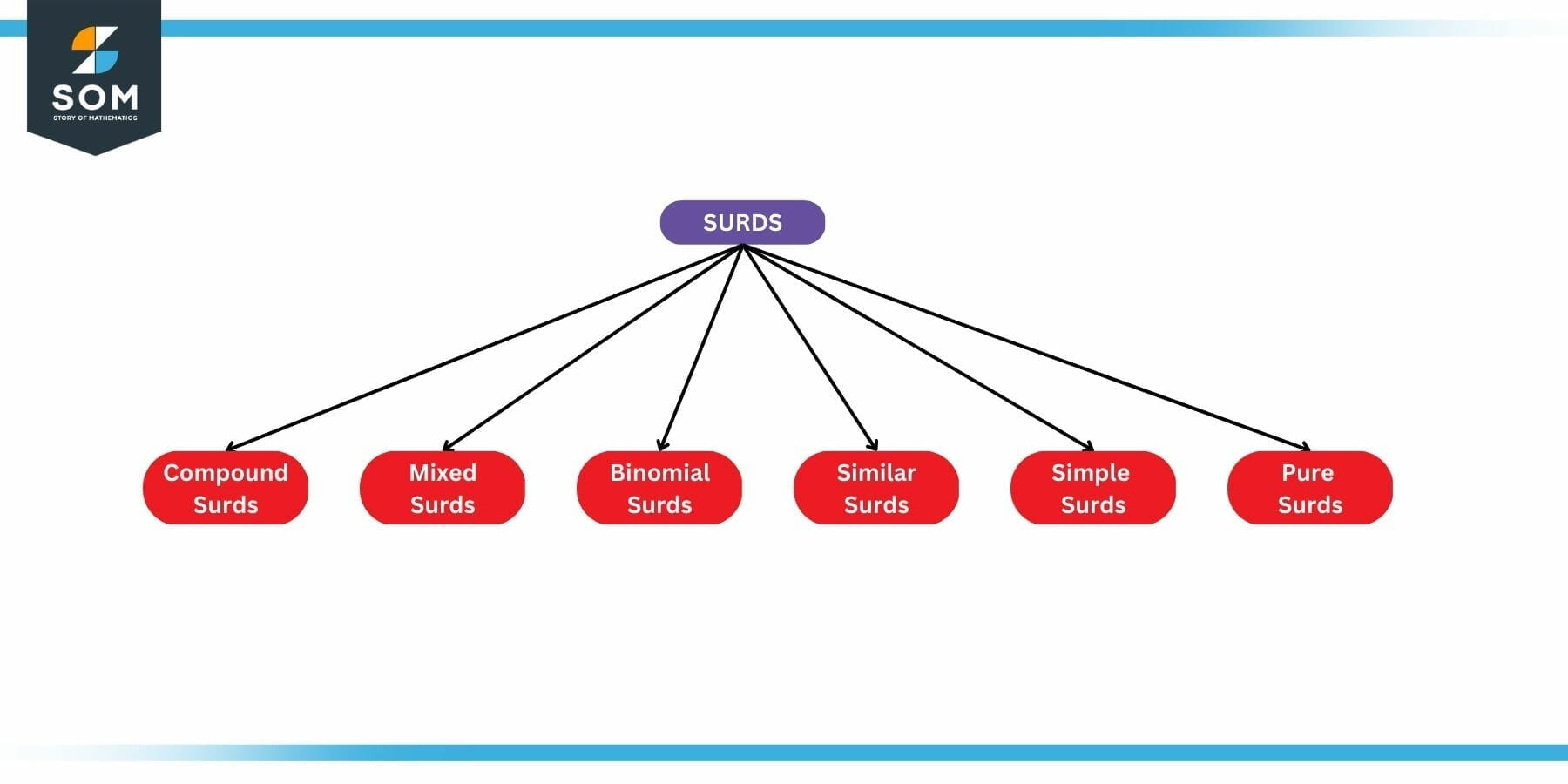
Figure 2: Types of Surds

History of Surds

The concept of surds was initially proposed by the Ancient Greeks, who studied the properties of right triangles and discovered that some length ratios could not be expressed as simple fractions. These ratios were termed as surds and were represented by the square root sign, as explained by the above example.

Explanation of Surds

A specific type of irrational number that cannot be expressed as a simple fraction is called a surd. A square root is represented by the symbol $\sqrt{}$ (square root), which is then followed by a number. Because it is a non-terminating, non-repeating decimal. For example, the surd $\sqrt{2}$ signifies the square root of 2, which cannot be expressed as a simple fraction.

The concept can also be considered by way of rational numbers. In mathematics, a number is considered to be rational if it can be expressed as the ratio of two integers. However, a number is considered irrational if it cannot be expressed as the ratio of two integers. Surds are examples of irrational numbers.

In addition to square roots, there are a number of other types of roots, including cube roots (represented by the sign ∛), fourth roots (represented by the symbol ⁴√), and so on. However, square roots are the type of surd that is most usually explored.

One of the most important features of surds is that they cannot be expressed as straightforward fractions. They differ in this sense from rational numbers, which may be expressed as simple fractions. As a result, surds cannot be expressed as decimals with a finite number of digits. Instead, they are shown as non-terminating, non-repeating decimals.

Another key feature of surds is their capacity to be combined with other surds and rational numbers to form more complex assertions. For instance, the expression $\sqrt{2}$ + $\sqrt{3}$ combines two surds to represent the sum of the square roots of 2 + 3.

To summarize, surds are irrational numbers that cannot be expressed as simple fractions. They are frequently studied in mathematics, and their symbol is (square root$\sqrt{ }$). Surds have a variety of important properties, such as the fact that they cannot be expressed as simple fractions and that they may be combined with other surds and rational numbers to form more complex assertions.

In several areas of mathematics, such as geometry, algebra, and calculus, surds are also extensively employed.

Applications of Surds

In addition to their special properties, surds have many applications in geometry, algebra, and calculus. For example:

1. Calculus: Surds are used in calculus to obtain the derivatives of functions having square roots.
2. Geometry: Surds are a tool used in geometry to calculate the lengths of the sides of right triangles. It can further be used in many real-world contexts, including construction and surveying, as right triangle side lengths may contain surds. For instance, a surd may be found in the hypotenuse of a given triangle. Another example is when calculating the area of a circle involves using the square root of pi.
3. Trigonometry: Trigonometric operations like sine, cosine, and tangent may make use of surds when computing certain angles.
4. Physical measurements: Some physical measurements, like the distance between them, may require surds if the route linking the two locations is not straight.
5. Logarithmic operations: Operations like log base 2 or log base 10 may call for surds when working with certain values.

Among many others.

Some Famous Surds

Surds are very commonly seen in mathematics. However, some of these have gained significance over time. Following are some examples:

The Golden Ratio

The golden ratio (also known as the golden number, the golden fraction, or the divine proportion), which is often symbolized by the greek letter phi ( $\phi$ ), is the ratio between two numbers defined as follows:

Golden Ratio = $\phi$ = $ \dfrac{ 1 + \sqrt{5} }{ 2 } $

This ratio is significantly associated with the Fibonacci Series. It is widely used in trading strategies, finance, and modeling. This so-called golden ratio manifests itself in many natural phenomena, including animals, plants, celestial systems etc.

Figure 3: The Golden Ratio

The Quadratic Equation

The quadratic equation, or the 2nd order polynomial, is used to model many real-world objects and phenomena. It also serves as the basis for parabolic, hyperbolic, elliptical, and circular shapes. The solution to such equations very often results in roots that are actually surds.

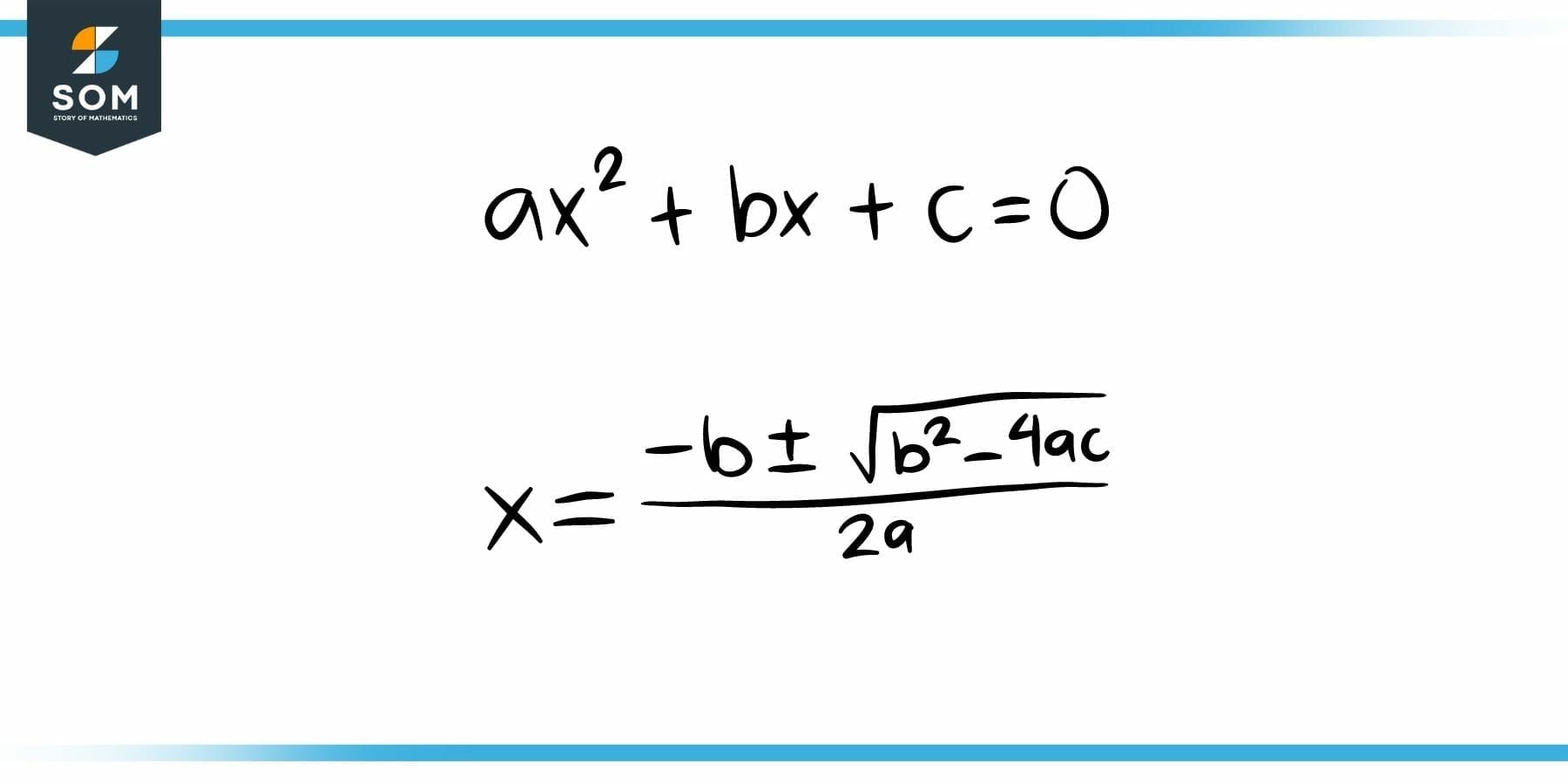
Figure 4: The Quadratic Equation

Key Features of Surds

Some key properties of surds are as follows:

• Irrationality: Since surds are irrational numbers, they cannot be expressed as simple fractions.
• Non-terminating: Surds cannot be expressed as a finite decimal since they are treated as non-terminating, non-repeating decimals.
• Simplification: Finding the optimal square roots of a surd’s values will make it easier to understand.
• Addition and subtraction: Surds can be added to and subtracted from other surds and rational numbers to form more complex statements.
• Division and Multiplication: Division and Multiplication of Surds may be made simpler by applying the exponent and square root methods.

There are quite a few others, but these are common ones you are likely to use.

Mathematical Rules for Solving Surds

Working with surds requires the ability to convert them into more basic forms. For instance, since $\sqrt{2 \times 2}$ equals $\sqrt{4}$, the surd $\sqrt{4}$ can be reduced to 2. Just as the surd $\sqrt{9}$ may be reduced to 3 since $\sqrt{3 \times 3}$ = $\sqrt{9}$.

Since surds are very common in many mathematical problems and numerical questions, some important rules may ease their solution. Following are some commonly used mathematical rules or so-called surd identities:

\[ \sqrt{x \times y} = \sqrt{x} \times \sqrt{y} \]

\[ \sqrt{ \dfrac{x}{y} } = \dfrac{ \sqrt{x} }{ \sqrt{y} } \]

\[ \dfrac{x}{\sqrt{y}} = \dfrac{ \sqrt{x} \times \sqrt{y}}{ y } \]

\[ x \sqrt{z} \pm y\sqrt{z} = ( x \pm y ) \sqrt{z} \]

Numerical Examples of Surds

(a) Multiply the surds $\sqrt{2}$ and $\sqrt{5}$.

(b) Divide the surd $\sqrt{8}$ by $\sqrt{2}$

(c) Simplify the surd $\sqrt{2} + 5 \sqrt{2}$

Solution

Part (a)

\[ \sqrt{2} \times \sqrt{5} = \sqrt{2 \times 5} = \sqrt{10} \]

Part (b)

\[ \dfrac{ \sqrt{8} }{ \sqrt{2} } = \sqrt{ \dfrac{ 8 }{ 2 } } = \sqrt{ 4 } = \pm 2 \]

Part (c)

\[ \sqrt{2} + 5 \sqrt{2} = (1 + 5) \sqrt{2} = 6 \sqrt{ 2 } \]

All images were created with GeoGebra.

Superscript Definition < Glossary Index > Surface Definition