JUMP TO TOPIC
Superscript|Definition & Meaning
Definition
A letter or number is said to be in superscript if it is smaller than and placed slightly above the rest of the text. We use superscripts to denote exponentiation (x2) and powers (2). These are pronounced “x Super 2,” “x squared,” or “x to the power 2.” It is also used in other, more advanced contexts to represent indices (not powers).
What Is Superscript?
“Superscript” refers to a number or variable written in a smaller script to the top right of another number or variable. According to this interpretation, a superscript is a superscript.
For instance, the letter I that appears in the word “5i” is a superscript. x2 is yet another example of a superscript. In this illustration, x denotes a value that cannot be determined, and the superscript is 2. In the equation x3 – xh, there are two superscripts; nevertheless, only the value directly to the left of each superscript is affected by those superscripts.
In the fields of mathematics and science, labels are written using superscripts. They are a shorthand notation employed in mathematics, and the context in which the superscript number, or variable, is used reveals the meaning of the shorthand notation.

Figure 1: Representation of superscript.
Uses of Superscript
The use of superscripts as exponents is among the most common applications of notation in mathematics. The repeated multiplication of a number can be written out more concisely using an exponent tool. As an illustration, the digit six in the number 76 instructs the reader to complete the multiplication 7∗7∗7∗7∗7∗7
Denoting derivatives is yet another typical application of superscripts. In calculus, a derivative is a method for calculating a function’s instantaneous rate of change. A superscript is a notation that provides a concise representation of the number of derivatives that need to be taken.
For instance, to differentiate f(x) twice is indicated by the notation f2(x), and to differentiate h(z) three times is indicated by the notation h3(z). Although these are the two most prevalent applications of superscripts in mathematics, they express various concepts throughout practical mathematics and science. Some examples of these concepts include isotope charge, electric charge, and contravariant tensors.
What Purpose Does the Superscript Serve in Research?
The use of superscript referencing would make it possible for scholars to recognise patterns in the body of published work that otherwise would not be readily apparent.
Difference Between Superscript and Subscript
The phrase “superscript” refers to numbers or characters printed in a lower typeface at a level higher than the main text. For example, “What is 22?” would be written in “superscript.”
“The term “subscript” refers to numbers or letters placed in a smaller typeface at a level lower than the main text. For example, “H2O” is written in a subscript.

Figure 2: Representation of the difference between subscript and superscript.
Exponent Superscripts
A “superscript” is a numerical value written above the standard line of text and, typically, in a lower point size than the surrounding text. In mathematics, the use of superscripts to express an exponent or a lifting to power is very prevalent. In mathematics, superscripts can be used for various purposes, such as calculating exponents. Superscripts can be present at the right or left of a sign or set of symbols; nevertheless, they never appear immediately above or below the symbols themselves.
When reading braille, the level change-up indicator is utilised to determine whether or not the item that comes after is in the superscript position. The next thing on the agenda is the magnitude of the level change-up indication. If an object appears immediately after the indicator that the level has changed, it is classified as belonging to either one of the following categories:
A complete number consists of the initial numeric symbol and any symbols that follow it within the numeric mode that was just established (which would include any interior decimal points, commas, separator spaces, or simple numeric fraction lines).
A complete general fraction that is surrounded by markers for fractions.A whole radical remark, wrapped among radical indications.
- A bow and arrow.
- A form is chosen at random.
- Any expression surrounded by a set of matching parentheses, brackets, or braces, whether round or square.
Any statement that is surrounded by the braille grouping indicators.
If none of those as mentioned above circumstances applies, the object in question is merely the following solitary symbol. Dots three and five serves as indicator for changing the braille level. The dots one, two, and six make up the opening braille grouping symbol, and the dots three, four, and five make up the closing braille grouping symbol.
Because each of the three symbols has a meaning associated with grade 2, the symbols must be used in the grade 1 method. Either the numeric indication or the grade 1 indicators are used to set the mode to Grade 1. The numeric mode is exited when the level change-up indicator is activated. A numeral located in the superscript position must be utilised in conjunction with the numeric indicator.
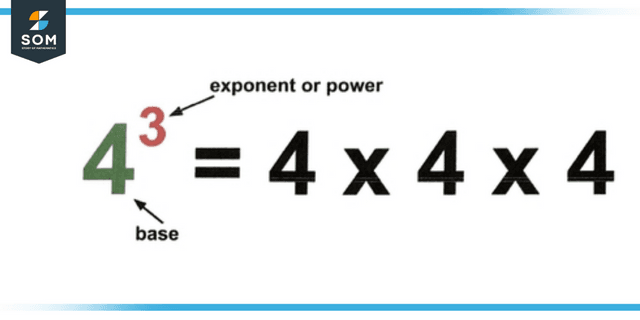
Figure 3: Representation of exponent superscript.
What Is the Proper Way to Type a Subscript?
A subscript can be typed using a keyboard if the appropriate keys are pressed. Hold down the Ctrl and Alt keys while pressing the ‘-‘ key to type a subscript on a keyboard. This will produce the subscript.
How To Write a Number That Has a Superscript?
The use of a keyboard allows for the creation of superscripts. When typing a number with a superscript keyboard, you must hold down the Control and Alt keys while concurrently pressing the plus sign key.
Examples of Superscript Usage
Example 1
Write the following term using only exponents. Simplify where possible.
(x-8 * 33)/ (4-2 * y2)
Solution
(x-8 * 33)/ (4-2 * y2)
In the above equation, the x-8 will come in the denominator and will become x8. The same is the case with 4-2. We will move it to the numerator, and it will become 42.
= (42 * 33)/ (x8 * y2)
As we know, 4 raised to power 2 is 16, and 3 raised to power 3 is 27.
16 * 27/ x8 * y2 = 432/ x8 * y2
Example 2
What is 67?
Solution
It can be written as:
6 * 6 * 6 * 6 * 6 * 6 * 6 = 279936
All images/graphs are created using GeoGebra.
