Symmetry|Definition & Meaning

What Is Symmetry?

A form or an object is said to have symmetry if it can be sectioned off into two halves that are mirror images of one another. When something is symmetrical, one half of the shape is a mirror image of the other half. 

The line of symmetry refers to the imaginary axis or line along which the image can be pleated to obtain the symmetrical halves. If you fold the figure along this line, you will get two identical halves.

If it is possible to separate a shape into two or more identical pieces that can then be reassembled in an orderly fashion, we call such a shape symmetric.

For instance, if you have a sheet of paper and are told to cut out a “heart” from it, you need to fold the paper in half, draw one-half of the heart at the fold, and then cut it out to discover that the other half of the heart exactly matches the first half. The cut-out shape of a heart is a demonstration of symmetry.

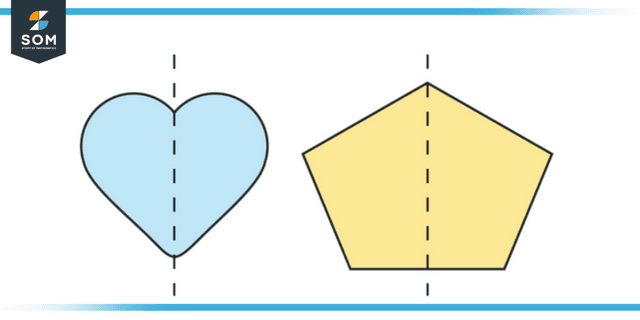
Figure 1: Representation of symmetry of different shape.

According to the mathematical definition of symmetry, “symmetry is a mirror image.” For something to be considered symmetrical, it must be possible to turn or mirror the shape so that the resultant image is equal to the original. Patterns contain symmetry in their design. It is a balanced and proportionate similarity seen in two halves of an object, indicating that one half is alike with the other part.

Additionally, it is a similarity that can be discovered in an object. We encounter symmetrical items regularly in our daily lives, in works of art, and in the built environment.

Line Symmetry

A symmetry line is a line that halves an object into two parts that are mirror images of one another. If we have a star that may fold into two halves. When an image is folded in half along its line of symmetry, the resulting halves are identical to one another when viewed from either side. The term “axis of symmetry” refers to this particular line of symmetry.

According to the direction in which it runs, the line of symmetry can be classified as either:

• Vertical Line of Symmetry
• Horizontal Line of Symmetry
• Diagonal Line of Symmetry

Vertical Line of Symmetry

A line that extends down vertically and divides an image into two parts identical to one another is called a vertical line of symmetry. For instance, if the shape can be cut along a straight line to create equal pieces. In this particular instance, the line of symmetry will be horizontal.

Horizontal Line of Symmetry

When a shape is split horizontally, i.e., sliced from right to left or vice versa, the horizontal line of symmetry separates the shape into two equal parts. For instance, if the shape can be cut horizontally in such a way that it creates two halves when the shape is split in half. When anything like this happens, the line of symmetry will be horizontal.

Diagonal Line of Symmetry

Whenever split across the diagonal corners, a shape is symmetrically divided into two halves similar to one another along a diagonal line of symmetry. For instance, we can create two halves by slicing the square shape through the middle of each corner. In this particular instance, the line of symmetry takes the form of a diagonal.

These things have one, two, or more two lines of symmetry.

• One line of symmetry
• Two lines of symmetry
• Infinite lines of symmetry

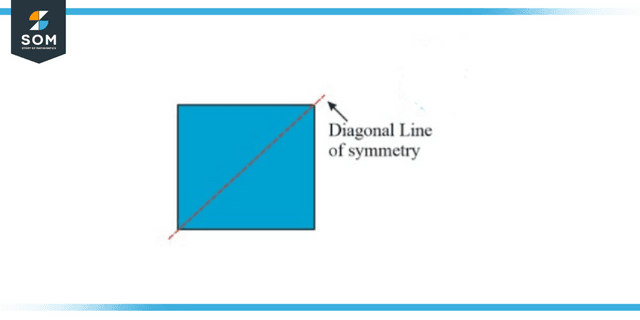
Figure 2: Representation of diagonal line of symmetry

One Line of Symmetry

Figures are only considered symmetrical about one axis if they have only one line of symmetry. It could be horizontal, it could be vertical, or it could be diagonal. For instance, the letter “A” has one line of symmetry, a line of symmetry that runs vertically through the middle of the letter.

Two Lines of Symmetry

Figures that only have symmetry about two lines of symmetry are said to have two lines of symmetry. The lines could be horizontal, vertical, or even diagonal from one another. Consider the rectangle as an example; it contains two lines of symmetry, one vertical and one horizontal.

Infinite Lines of Symmetry

Only roughly two lines of symmetry can be found in figures with an infinite number of lines of symmetry. The lines could be horizontal, vertical, or even diagonal from one another. Consider the rectangle as an example; it contains two lines of symmetry, one vertical and one horizontal.

Types of Symmetry

You can observe its symmetrical properties when you slide, turn, or flip an object. There are four distinct kinds of symmetry, each of which can be found in different contexts.

symmetry in terms of translation

• Symmetry based on rotation
• Reflexive symmetry
• Glide symmetry
• Symmetry in the Translation

Translational Symmetry

Translational symmetry is when an object is transferred from one point to another while maintaining the same orientation in both the forward and backward motion. In other words, the slide of an entity about an axis is the definition of what is known as translation symmetry.

Rotational Symmetry

It is referred to as rotational symmetry, also known as radial symmetry, when an item is rotated in a specific direction around a point.

When a shape is spun about in such a way that it retains its original form, we say that the shape possesses rotational symmetry. The order of symmetry refers to how the item coincides with itself when it is rotated. The rotational symmetry angle is the minimum angle at which the image may be rotated to coincide with itself.

There are a lot of different shapes in geometry that illustrate rotational symmetry. Examples of figures demonstrating rotational symmetry include the circle, the square, and the rectangle.

Reflexive Symmetry

One sort of symmetry is known as reflective symmetry, which is often referred to as mirror symmetry. In reflective symmetry, one half of an item mirrors the other side of the object. For illustration purposes, a human face’s left and right sides are typically identical.

Figure 3: Representation of reflexive symmetry

Glide Symmetry

The transformations of translation and reflection come together to generate the symmetry known as glide symmetry. The nature of a glide reflection is such that it is commutative, and changing the sequence in which the combinations are performed does not affect the outcome of the glide reflection.

Trivial Points About Symmetry

Mirrors within a kaleidoscope are responsible for creating visuals that feature various lines of symmetry. The number of lines of symmetry is determined by the angle at which the mirrors are placed.

We have encountered several symmetrical things in our daily lives, such as rangolis and kolams. The designs of rangoli sometimes feature outstanding examples of symmetry in their layouts. These patterns are well-known in India since they are both distinctive and symmetrical. They illustrate the colorful aspects of the scientific study of symmetry.

Examples of Symmetry

Example 1

If y= x² + 4x + 3, find the axis of symmetry of the graph of y by using the appropriate formula.

Solution

y = x² + 4x + 3 equation is given to us.

The axis of symmetry of a quadratic equation is given by the formula:

x = -b/2a

For a quadratic function in standard form y = ax² + bx + c, the axis of symmetry is a vertical line,  x = -b/2a. Here, a = 1, b = 4 and c = 3. Putting the values of a and b:

x = -(4) / (2 * 1)

= -4/2

= -2

Evidently, the axis of symmetry is at x = -2.

Example 2

If y= 5x² – 7x + 9, then find the axis of symmetry for the function y = f(x) by using the appropriate formula.

Solution

y = 5x² – 5x + 9

Now compare the given equation with the standard form:

y = ax² + bx + c,

a = 5, b = -5, c = 9

And the axis of symmetry is a vertical line:

x = -b/2a

After putting the values of a and b:

x = – (-5) / 2(5)

= 5/10

= 0.5

Therefore, the axis of symmetry is x = 1/2 or 0.5.

Example 3

Given that the axis of symmetry of the equation y = gx² – 14x – 10 is 4, find the value of g.

Solution

We are given the following:

y = gx² – 14x – 10

4 is the axis of symmetry. Since y = ax² + bx + c, the axis of symmetry is a vertical line:

x = 4

Here, a = g, b = -14, c = -10. According to what’s given:

= -b/2g = -b/2g = 4

= -(-14)/2g = 4

= 14 = 8g

g = 14/8 = 7/4

Thus, g = 7/4 or 1.75.

All images/graphs are created using GeoGebra.

Survey Definition < Glossary Index > Table Definition