Terminating Decimal|Definition & Meaning

Figure 1 shows different examples of terminating decimals.

Figure 1 – Terminating Decimals with One, Two, and Three Decimal Digits

Conversion From Fraction to Decimal Form

To convert a fraction into decimal form, the numerator(dividend) is divided by the denominator(divisor). Figure 2 shows the conversion of the fraction 1/8 into decimal form by long division, giving the quotient as 0.125. 

Figure 2 – Process of Converting a Fraction into Decimal Form by Long Division

Rational Numbers

A rational number can be written as u/v where v ≠ 0.  The form u / v is also known as a fraction. The numerator u and denominator v are integers, but the denominator is non-zero.

If a rational number is divided, the answer will always be in decimal form. This decimal form can be a terminating or a repeating decimal. Some examples of rational numbers include 1/5, 2/7, 9/4, and 1/7. These fractions can be written in decimal form as:

1/5 = 0.2

2/7 ≅ 0.29

9/4 = 2.25

1/7 ≅ 0.142857

The approximation “≅” sign indicates that the decimal digits are rounded off or approximated.

The set of rational numbers, usually denoted by Q, is a subset of real numbers R. The integers Z, natural numbers N, and whole numbers W are the subset of the rational numbers as every integer, natural number, and whole number can be written in the form of u/v.

Non-terminating and Recurring Decimal

A non-terminating and recurring decimal is a rational number whose decimal digits go on forever, and there is a repetitive pattern in the decimal digits. A bar is placed on top of the repeating decimal digits.

For example, 10/3 is a non-terminating and recurring decimal equal to 3.333… which can also be written as 3.$\bar{3}$.

Standard Form

For a rational number, the standard form is the simplified form of u/v. It means that the divisor and the dividend have no common factors other than one.

For example, the rational number 100/40 has 10 as the common factor. Dividing the numerator and denominator by 10 gives:

100/40 = 10/4

The fraction 10/4 still has 2 as the common factor. Dividing 10/4 by 2 gives:

10/4 = 5/2

Hence, the standard form of 100/40 is 5/2, which is a terminating decimal equal to 2.5.

Types of Fractions

There are two types of fractions: proper and improper fractions.

Proper Fractions

Proper fractions are the type of fractions whose numerator is smaller than its denominator. For example, 6/10, 3/20, and 8/15 are proper fractions whose decimal forms are:

6/10 = 0.6

3/20 = 0.15

8/15 = 0.53

All the above proper fractions are terminating decimals.

Improper Fractions

Improper fractions are the fractions whose numerator is greater than its denominator. For example, 50/16, 14/8, and 66/12 are improper fractions that can be written in decimal forms as:

50/16 = 3.125

14/8 = 1.75

66/12 = 5.5

All the above decimals are terminating. Figure 3 shows examples of proper and improper fractions with their terminating decimal forms. But not all proper and improper fractions are terminating decimals.

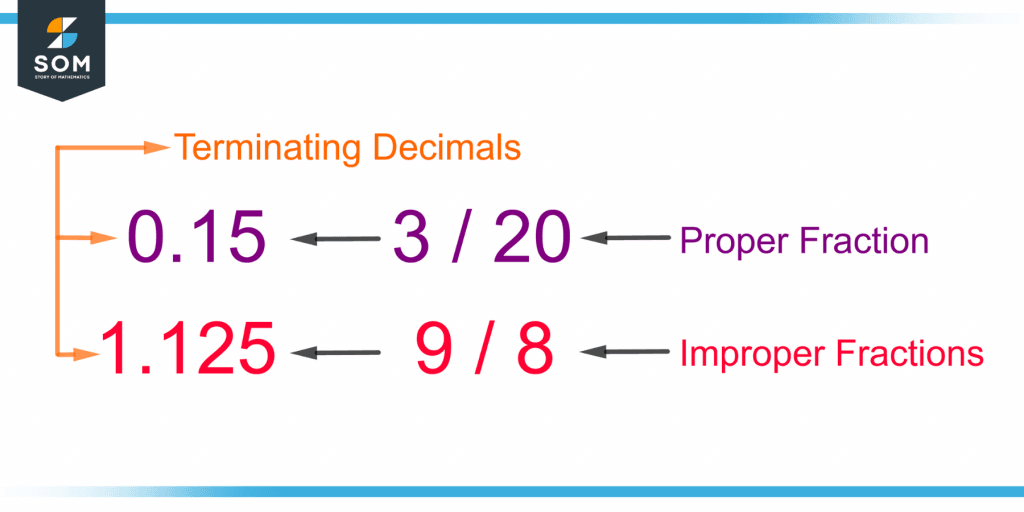
Figure 3 – Proper and Improper Fractions as Terminating Decimals

Arithmetic Operations on Terminating Decimals

The different arithmetic operations that can be performed on terminating decimals are addition, subtraction, multiplication, and division.

Addition

Two or more terminating decimals can be added by aligning the decimal points vertically. The empty spaces are filled with zeros. The numbers are added simply as any other addition. The decimal point in the obtained sum is placed vertically, similar to the decimal addends.

Subtraction

One terminating decimal is subtracted from the other by the same vertical alignment of the decimal points. The subtraction is carried out with zeros assumed in the empty place. The decimal is placed in the same position as in two decimals being subtracted.

Figure 4 shows the addition and subtraction of two terminating decimals.

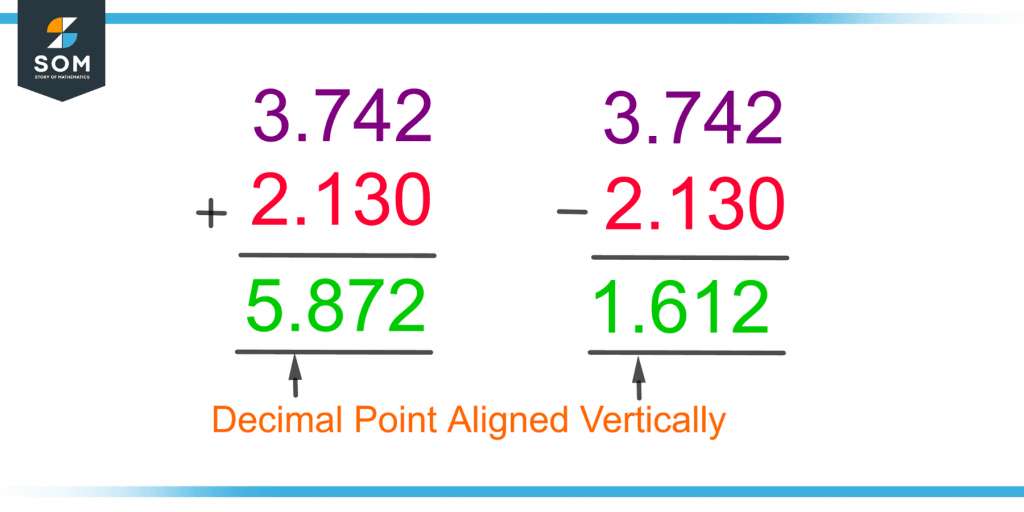
Figure 4 – Addition and Subtraction of Two Terminating Decimals

Multiplication

The multiplication of two decimal numbers is carried out by considering that there is no decimal point in the numbers. After the product is attained, the number of decimal digits of both decimal numbers is counted.

Starting from the right of the product and going towards the left, the decimal point is placed according to the total number of decimal places in the multiplicand and the multiplier.

Figure 5 shows the multiplication of two terminating decimal numbers.

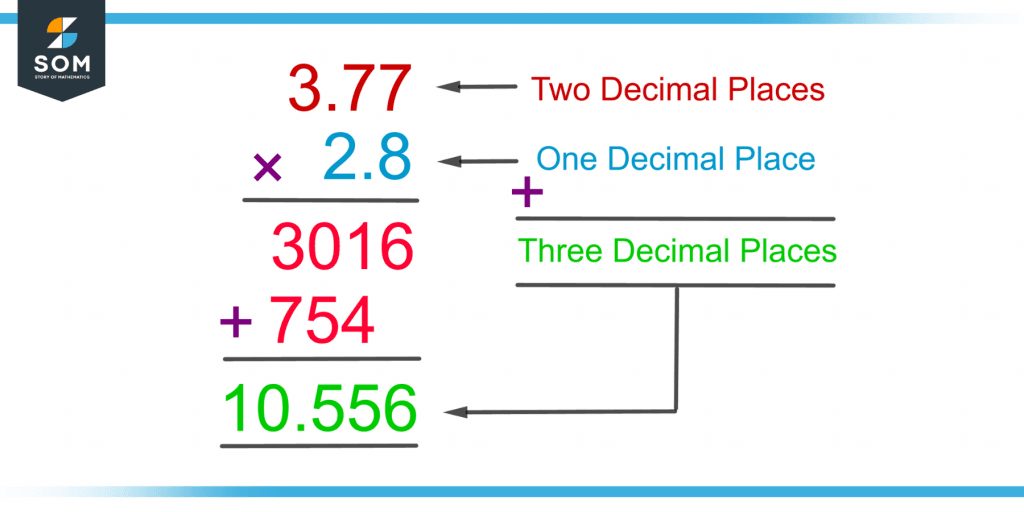
Figure 5 – Multiplication of Two Terminating Decimals

Division

The division of two terminating decimal numbers is performed by converting the divisor into a whole number.

This is done by moving the decimal point in the divisor to the right, making it a whole number. Also, the dividend’s decimal point is moved the same number of places as the divisor. To move the decimal point to the right means to multiply the number by 10 or 100.

Then, the dividend is divided by the divisor by the same long division method. The decimal point in the quotient is placed above the dividend’s decimal point.

For example, in 33.856/2.3, 33.856 is the dividend, and 2.3 is the divisor. The divisor is multiplied by 10 to remove the decimal point as:

2.3 ✕ 10 = 23

Similarly, the dividend is also multiplied by 10 to balance the fraction as:

33.856 ✕ 10 = 338.56

The long division of 338.56/23 is shown in figure 6.

Figure 6 – Division of Two Terminating Decimals

Rounding Off Terminating Decimals

A rounded-off decimal is close to its original value. The terminating decimals are rounded off to a certain degree of accuracy. Rounding off terminating decimals helps to estimate the result faster and in an easier way. For example, a student’s percentage is usually rounded off to estimate a student’s performance in a class.

A terminating decimal can be rounded off to the tenths, hundredths, or even thousandths place. It can also be rounded to a whole number by rounding it off to the tens or hundreds place. To round up or down to a certain place, e.g., the tenth or hundredth place, the number following the place is checked.

Rounding Up

If the number following or next to a certain place, e.g., the tenth place, is 5 or greater than 5, the decimal is rounded up.

For example, in the terminating decimal 35.27, 2 is in the tenth place, and 7 is in the hundredth place. To round this decimal to the tenth place, the number next to the tenth place, i.e., 7, is checked. As it is greater than 5, the decimal is rounded up. So, the number becomes 35.3.

A decimal can also be rounded to the hundredth place. In the number 42.685, 8 is in the hundredth place. To round it off to the hundredth place, the number next to the hundredth place, i.e., 5, is checked. As it is 5, so the decimal is rounded up. The decimal becomes 42.69.

Rounding Down

If the number next to a certain place, e.g., the thousandth place, is less than 5, the decimal is rounded down.

For example, in the terminating decimal, 64.8652, the number 5 is in the thousandth place. To round it to the thousandth place, the number following the thousandth place, i.e., 2, is checked. As it is less than 5, the decimal is rounded down. So, the decimal becomes 64.865.

Properties of Terminating Decimal

The following are the properties of a terminating decimal:

The result of the multiplication of a terminating decimal with another terminating decimal is always a terminating decimal.

The terminating decimal remains the same if both the numerator and denominator are multiplied by the same number in its fraction form.

If a zero is added to a terminating decimal, the result will be the terminating decimal.

Irrational Numbers

The numbers which cannot be written in u/v form are known as irrational numbers. For example, $\sqrt{2}$, $\sqrt{7}$, and $\sqrt{1.6}$ are all irrational numbers.

Non-terminating and Non-recurring Decimal

Irrational numbers are non-terminating and non-recurring. It means that they can be written in infinite decimal digits, and no repetition in a digit pattern is observed. For example, the Euler’s number “e” equal to 2.7182818… is a non-terminating and non-recurring irrational decimal.

Examples of Terminating Decimals

Example 1

Which of the following numbers are terminating decimals?

1.25, $\sqrt{5}$, 2.14

Calculate the sum and product of the two terminating decimals.

Solution

The terminating decimals are 1.25 and 2.14 as $\sqrt{5}$ is equal to 2.23606797… The sum and the product of 1.25 and 2.14 are calculated in figure 7.

Figure 7 – Example of Addition and Multiplication of Two Terminating Decimals

Hence, the sum of 1.25 and 2.14 is 3.39, and their product is 2.6750.

Example 2

Round off the terminating decimal 82.68 to the tenth place, 73.542 to the hundredth place, and 27.8359 to the thousandth place. Are they rounded up or down?

Solution

The number 82.68 is rounded to the tenth place, i.e., 6 as 82.7, as the number following the tenth place, i.e., 8, is greater than 5. It is rounded up.

The number 73.542 is rounded to the hundredth place, i.e., 4 as 73.54 as the number following the hundredth place, i.e., 2 is less than 5. It is rounded down.

The number 27.8359 is rounded to the thousandth place, i.e., 5 as 27.836 as the number following the thousandth place, i.e., 9 is greater than 5. It is rounded up.

All the images are created using GeoGebra.

Term Definition < Glossary Index > Tessellation Definition