Tessellation|Definition & Meaning

Definition

Tessellation refers to covering a given surface with a pattern of flat shapes (either repeating or non-repeating) in such a way that no shape overlaps another, and there’s no gap between any two shapes. Real-life examples include the pattern of a brick wall (its surface is tessellated rectangles) and many types of flooring, which is why tessellation is sometimes also called tiling.

Figure 1 – Triangle-based tessellation.

As shown in the figure above, triangles can be used to make a tessellated pattern. But you can also make them by mixing different geometric shapes (e.g., hexagons and squares), to make tessellating patterns. The only rule is that all of the sides must fit together perfectly, with no empty spaces or overlap.

What It Means

The word “tessellation” originates from the Latin verb tessellate, which translates to “to pave,” or the word “tessella,” which refers to a little, rectangular stone. There is evidence that tessellations were used in a variety of ancient cultures across the world.

They frequently exhibit certain qualities that are tied to their place of origin in some way. Tessellations had been tracked all the way back to the ancient civilizations, where they were first discovered (around 4000 BC).

Tessellations, which are miniature quadrilaterals used in computer games and in the construction of mosaics, were exploited by the ancient Greeks. The Alhambra Palace in Granada, which is in the southern region of Spain, is an example of a Muslim edifice that hints at the presence of tessellations. In addition, the tessellations that are used in architecture may be seen at Fatehpur Sikri.

These days, tessellations are employed for the floors, walls, and ceilings that are found inside buildings. They are used rather frequently in works of art, patterns for clothing, designs for pottery, and blown glass windows.

Deep Dive Into Tessellation

Tessellations are regular patterns created by the repetition and seamless joining of flat forms. The forms themselves need not be identical, but the patterns should be repeated. Tiling is another term for tessellation.

The name “tessellation” comes from the Greek word “tesseres” which translates to “four.” This phrase means the four corners of a square, which was the first form to be tiled.

The term “tessellation” refers to a collection of two-dimensional shapes that are seamless and completely interconnected with one another. Floor tiles provide a common example of geometrical patterns that can be found in real life. However, why are certain forms able to tessellate while others are not?

A pattern that is created by repeatedly using the same regular polygon is called a regular tessellation. A polygon is said to be regular if all its internal angles and sides are the same measurement.

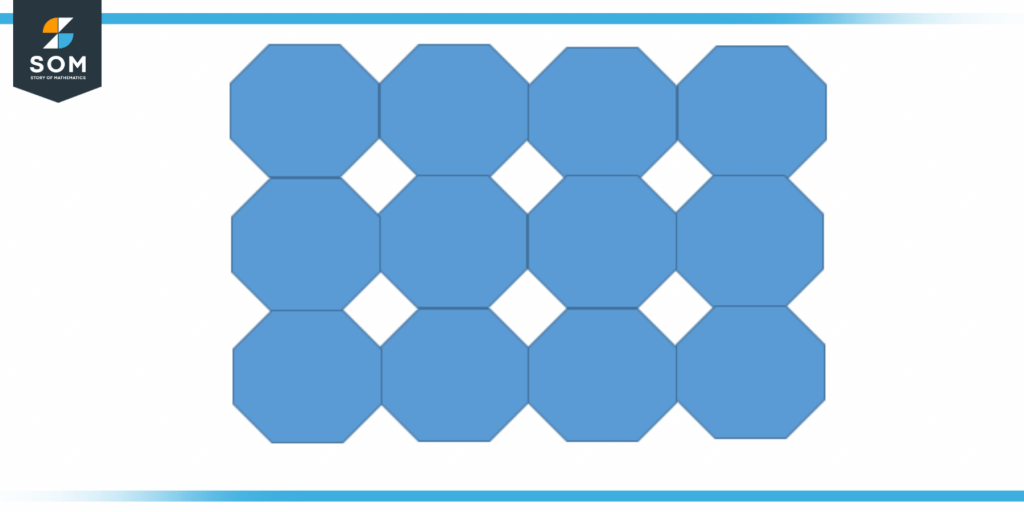
Figure 2 – Hexagon-Square paired semi-regular tessellation

It follows that there are only three distinct types of regular tessellations: those constructed from squares, equilateral triangles, and hexagons.

The point where two shapes meet, also known as the corner point, is referred to as the vertex. You can give a name to a tessellation by focusing on the vertex and noting the side of all the structures that converge at the vertex at the same time.

When two or even more polygons meet at a point in a tessellation, or when two or even more polygons meet at a certain vertex, the inner angles should add up to 360°. Only triangles, squares, and hexagons, which are the only shapes with equal sides and angles, can make a tessellation on their own.

There are only three types of shapes that can make tessellation patterns by themselves. These are squares, hexagons, and equilateral triangles.

This happens because these shapes can fit together without any gaps, and they will all look the same in the pattern. A honeycomb is an example of an everyday object with a hexagonal tessellation pattern.

Figure 3 – Irregular tessellation

Here in the figure above, the recurring circular shape is repeating one after the other. However, they leave gaps between them, so it’s not a regular tessellation.

Evidently, some shapes, like circles, can’t tessellate because they don’t fit together perfectly. They might be components of a tessellation, and the spaces between them could be seen as a different kind of shape. This is called an irregular tessellation.

This is also true of a pentagonal tessellation, in which pentagons can fit together, but only when they change size and shape. Regular pentagons that are all the same can’t make tessellations on their own.

Tessellation in Real Life

Tessellations and the various ways that they can be employed in building design because of their malleability and potential application in the visual arts and built environment, tessellations are an essential component of the mathematical discipline of mathematics. One artist, MC Escher, who was from the Netherlands, is known for incorporating a lot of intricate tessellations into his work.

Tessellations are utilized extensively in regular things, particularly in the construction of walls and structures. They are a component of a branch of mathematics that frequently gives the impression that it is simple to understand, but research shows that they are, in fact, quite hard.

Classification of Tessellation

A structure that is created by repeatedly using a regular polygon is referred to as a normal tessellation. Consider the fact that all the angles and aspects of a regular polygon are the same. There are three different shapes that can be used to create regular tessellations: an evenly spaced triangle, a rectangular shape, or a hexagon.

Geometric shapes can be given names based on the machines that were used to create them. You will start by picking a vertex from within the pattern. A vertex is a nook within a polygon, so keep in mind what this means. It makes no difference which vertex you choose to use. After that, select the polygons that surround it based on the total number of facets that each one possesses.

Example Problem on Tessellation Patterns

Explain how a regular polygon can form a pattern that tessellates.

Solution

Let’s get some work in and call it that. First, we pick a vertex from within the pattern to work with. After that, we consider the number of polygons that converge at that vertex. There is a total of six. Every polygon can be represented as a triangle.

Because each triangle has three sides, this kind of tessellation is referred to as a 3.3.3 tessellation (see Figure 1, though due to slight drawing errors, it’s not a regular tessellation). Each number 3 denotes a triangle whose three sides converge at the apex.

Tessellations that are made up of or contain a greater number of regular polygons are referred to as semi-regular tessellations (see the Hexagon-square pair in Figure 2).

When we concentrate on the geometric shapes, we will notice that the pattern is produced by moving the triangle around the components of the hexagons in a certain way. The method we devised for giving names to tessellations leads us to the conclusion that this is a 3.3.6 tessellation. The six trees make up the hexagon, while the two triangles are made up of the trees themselves.

All the figures above are created on GeoGebra.