Theorem|Definition & Meaning

Mathematics is all about theorems. A proposition established as true by rigorous proof, a specific type of logical reasoning, is known as a theorem. The graphical elaboration on the concept of the theorem has been depicted in Figure 1 below: 

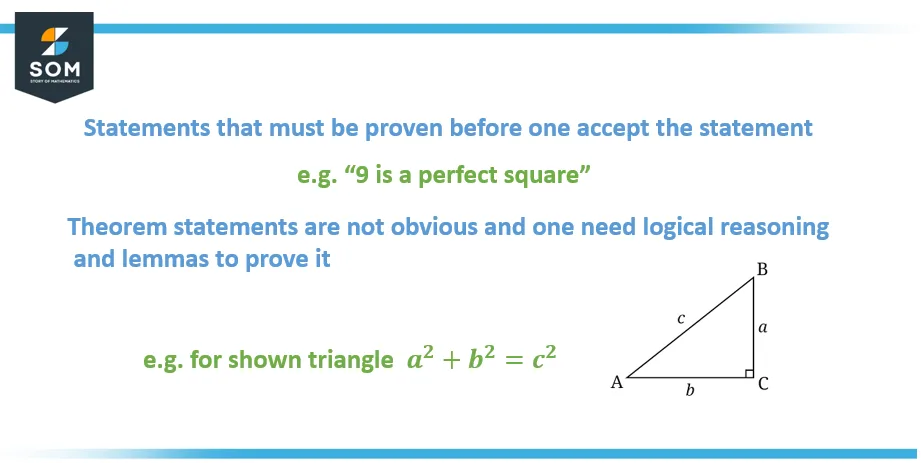
Figure 1: The concept of the theorem

Alternatively, a theorem is a strong logical argument that begins with assumptions we already know to be true and proceeds in manageable steps, each step building upon the one before it, which is the foundation of rigorous proof. If it is impossible for the first argument to be untrue while the second is true, then one statement follows from the other.

As an illustrative example, it follows that “Socrates is mortal” also follows from the statements “All Greeks are mortal, and Socrates is a Greek” because it is impossible for either assertion to be true without the other.

As a result, if we begin with statements that we already know to be true, then every statement that comes after must also be true. Once a theorem has been established, its authenticity is known for certain. A theorem can be disregarded by simply not understanding what it states.

Note that the argument used to prove a theorem is logical, and it shows that the theorem follows logically from the axioms and another theorem that has already been proven using the logical system’s inference rules.

Related Terminology

The goal of mathematics is to prove theorems. In pure mathematics, we examine issues that intrigue us on their own terms, seeking solutions by building on our existing knowledge and establishing theorems.

Depending on their significance or their connections to other theorems, theorems may go by a variety of names; lemma, corollary, Proposition, etc.

Lemma

A lemma is a theorem that is largely proven as a prelude to the proof of another theorem.

Corollary

A corollary is a theorem that naturally results from another theorem. When they are first introduced, theorems are frequently referred to as propositions.

Proposition

A mathematical statement that can either be true or false, such as “4 is greater than 5,” “an infinite set exists,” or “11 is prime,” is referred to as a proposition. Although there are several exceptions, mathematical logic can typically classify a claim as true or false given enough information (e.g., “This statement is false”).

One of the examples of the elaboration of Pythagoras’ theorem is depicted in Figure 2 below:

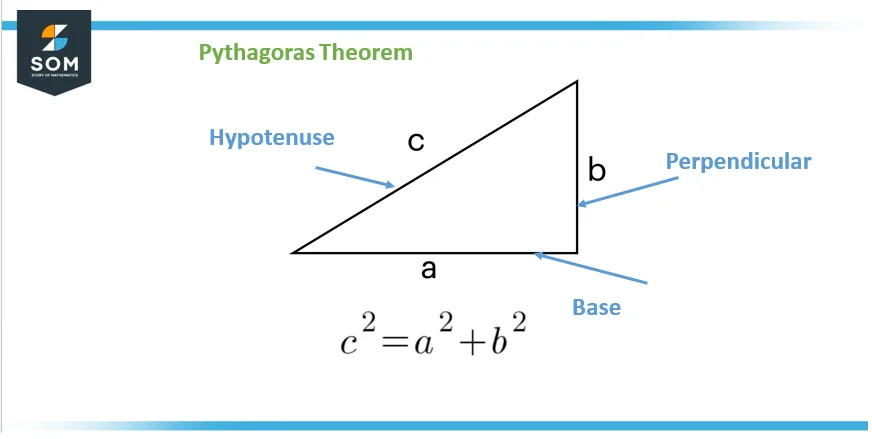
Figure 2: Pythagoras’ theorem

Axiom

A statement that is assumed to be true is referred to as an axiom, postulate, or assumption. It is used as the foundation for future deductive reasoning and argument.

Hypothesis

A hypothesis is a theory that could explain a law or another set of observations, and theories frequently take the shape of mathematical models, which are mathematical systems with structures designed to as nearly as possible mirror the behavior of the phenomena under study.

Theory

What one may refer to as a “theory” in daily life is completely unrelated to this. Our everyday, non-technical definition of “theory”—a basic hypothesis that may be tested—is considerably closer to this definition than the one used in science.

A student may have a “theory” about how to achieve a good grade, for instance, while a detective may have one about who did the murder.

In the scientific sense, these are not “theories” at all! A full scientific theory is never developed by one person alone since they are just too huge and complex. A scientific theory is a vast body of knowledge that combines numerous rigorous hypotheses and mathematical models and weaves them into an understandable explanation for the facts and laws that are readily apparent.

Theorems are proved, not theories. Before a theorem is proven, it is referred to as a conjecture in mathematics. Only thoroughly investigated hypotheses can be included in a scientific theory. A theory in science only contains well-founded assurance.

In mathematics, “theory” is used in a way related to “scientific theory,” indicating something like “the study of.” For instance, “knot theory” does not signify “a hypothesis about knots” but rather “the mathematical study of knots”; it is only a colloquial term for all of the relevant books, papers, theorems, and other works.

A mathematical theory comprises lemmas, theorems, and corollaries, as opposed to scientific theories, which are made up of tried-and-true assumptions and mathematical models. Both refer to disciplines of study in which a great deal is known, yet there is still more to learn; both are perpetually unfinished in the sense that there are constantly new theorems to be proved and new hypotheses to be verified.

Scientific Theory

We search for a collection of principles that offer a unified explanation for the numerous laws and facts we’ve gathered while testing and improving our hypotheses until we have a very high level of confidence in them.

We refer to a scientific theory as this level of a thorough explanation of a certain component of reality that includes numerous well-tested hypotheses and mathematical models and explains the various facts and laws we have observed.

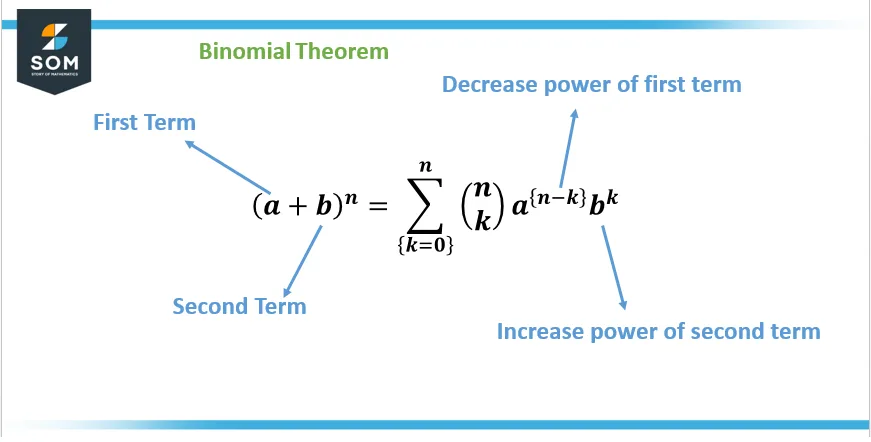
Figure 3: Binomial theorem

Applying Theorems to Real Problems

The process of applying theorems we can prove about the mathematical models to derive conclusions about the relevant real-world phenomenon is known as applied mathematics. Alternatively, Applied mathematics is the cornerstone of scientific knowledge.

Analyses can help us in the sciences to identify both facts and laws. A law is an assertion concerning the consistency of the facts as they are observed, such as “things fall when dropped.”

In order to create mathematical models that duplicate the data, scientists must make thorough observations about the world. A scientific model can be tested by predicting the outcomes of an observation using the model, then performing the observation and comparing the outcomes.

The model has to be improved if it cannot correctly predict the result of the observation; however, if the prediction of the model fits the observed, the model is compatible with the observation.

Although consistency with sufficiently repeated observations indicates that a model is a plausible option for an explanation of the phenomena, consistency with observation does not ensure that the model will always match the facts for every subsequent observation. A model is evaluated and improved over time, with further information being added via additional observations and tests.

Examples of Theorems in Mathematics

Give examples of any four theorems in mathematics and define their statements.

Solution

Following are four mathematical theorems and their definitions:

1. Euclidean geometry: This theorem states that “two parallel lines never intersect.”
2. Law of Cosines: This theorem states that “in a triangle, the square of the length of a side is equal to the sum of the squares of the lengths of the other two sides minus twice the product of the lengths of those two sides multiplied by the cosine of the angle between them.’
3. The Binomial Theorem: This theorem states that “the expansion of $(a+b)^n$, where a and b are constants and n is a non-negative integer, is given by the sum of the terms (n choose k) $a^{(n-k)}b^k$, where k ranges from 0 to n.
4. Fermat’s Last Theorem: This theorem states that “there are no non-zero integers x, y, and z that satisfy the equation $x^n$ + $y^n$ = $z^n$, where n is an integer greater than 2

All images/mathematical drawings were created with GeoGebra.

Tessellation Definition < Glossary Index > Thrice Definition