JUMP TO TOPIC
Thrice|Definition & Meaning
Definition
Three times any value is called “thrice” that value. It is a quick way of saying, “the product of multiplying x by 3 is y,” where we just say, “thrice x is y” or “y is thrice x.” For example, since 5 x 3 is 15, we can say that 15 is thrice 3. Sometimes, we also use the word tripled, as in “y is x tripled.”
What Does Thrice Mean?
In mathematical terms, thrice means multiplying any number with a quantity of three. Such terminologies are used in mathematical word problems in which relationships of multiple expressions are described. It simply means to add a given quantity three times with itself. Similar notions like once, twice, etc., are also used to represent such a relationship.
Thrice is a numerical term that is known as a multiplicative number used to represent a repetition of quantity.
Whenever an event or occasion happens thrice, it means the event is repeating itself the third time. This should not be confused with twice, which means two times; as they say, you should always think not twice but thrice before making a judgment or decision.
Thrice can also be used to indicate something is three times the size compared to another thing or if the value is three times or the intensity of something happening a third time in a row.

Figure 1 – The size of Jupiter is thrice that of Earth
The Origin of Thrice
Different numerical terms have different functions, but thrice and other multiplicative numbers like once and twice perform the same functions, but it should first be clear where these terms originate from.
The majority of mathematical expressions contain Latin or Ancient English bases. The words once, twice, and thrice all have Ancient English origins.
Once refers to an adjective meaning that comes from the medieval English letter “ones” and the ancient English letter “anes” (of one). It is frequently used to indicate periodicity, which is the occurrence of a phenomenon once and only once.
Once can also be employed to denote an earlier occurrence. For instance, “He was once a polite student.”. Here Once told us that the youngster used to be polite, but that isn’t the case now.
The second term twice or originally called ‘twise,’ is a combination of the ancient English words “twiges” and the medieval English words “twies” and “twizes.”
Since it is now clear what once and twice are, it becomes easy to predict what comes after that. If one follows the argument of the prior discussion, saying that thrice comes after twice would not be a bad answer; in fact, it is the right one. Just like the origin of once and twice, thrice comes from the same background and holds the exact meanings as did the previous two.
The use of the term thrice has now been relatively out of date, as compared to once and twice, but it is still fairly used in American and British literature.
Sometimes you could find thrice being used to denote a deliberately comedic or antique stereotype. Also, these terms come in handy as they are one word shorter than their counterpart, such as twice being used two times and thrice being used as three times; it becomes easy to just use the short form for better and fluent conversation. Despite being rarely used, you may come across words like thrice big or thrice removed in your daily life routine.
Other Types of Numerical Terms
Other than the multiplicative terms, there are many other numerical terms that are used in mathematics, some of which are
Cardinal Numbers
The numbers that are used to represent a quantity are cardinal numbers, such as one, two, and three. These distinct terms are used occasionally in our daily routines. As they represent simple quantities, their names are derived from ancient English vocabulary.
Collective Numerals
When we are obliged to represent sets and groups, we use collective numerals, such as twins, triplets, quadruplets, etc. Collective numbers have many subcategories, but the most common ones are the ones described above.
The music industry also uses these terms with a slight change as a duo, trio, and quartet. Other common terms used in our routines are dozen, pairs, etc., which are extensively combined with day-to-day belongings.
Composite Numerals
Such Numbers represent the origin of something or what it is composed of. As the name suggests, they are used to denote composition. It illustrates the concept that the item is made of a single term, two terms, or maybe even three terms. We call them unary, binary, ternary, and quaternary, and the list goes on. The most common one is binary, as it is used in every computer program.
Multiplicative Numbers
Once, twice, and thrice are multiplicative numbers, and we have discussed them thoroughly in the previous section. They are used to represent a repetition of something.
Some other common numerical terms are ordinal numbers, partitive numbers, ranking numbers, and reproductive numbers. All of these terms have distinct functionality and a distinct set of words contained in them.
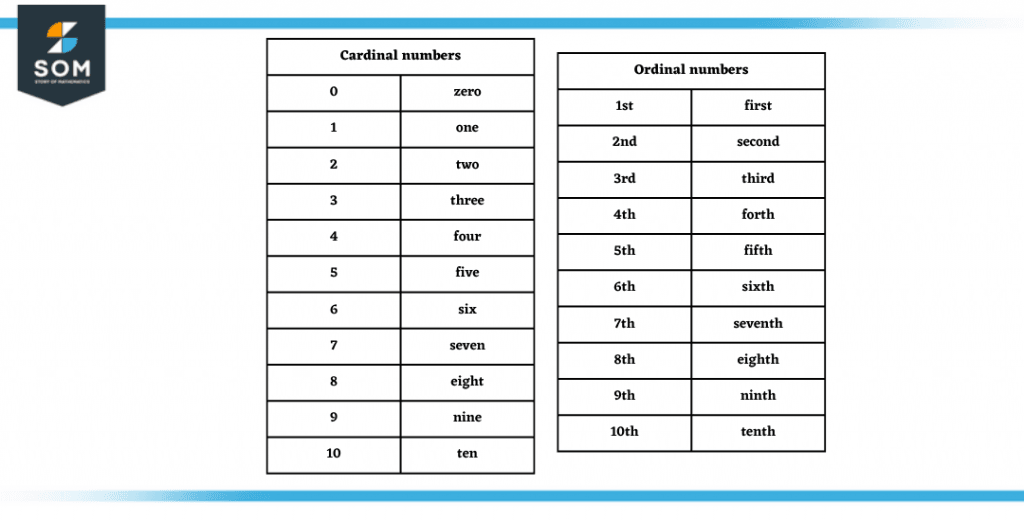
Figure 2 – Cardinal and Ordinal numeral systems
What Comes After Thrice?
Now we are much more aware of the different numerical terms, their functions, and the type of terms once, twice, and thrice. But one thing that is still missing is what comes after thrice.
Usually, the counting ends at thrice since there is not much available to follow it in succession. Also, according to the world dictionary, thrice has no successor. But a few terms have been known to be the continuation of thrice. The terms include quince, quarce, fourice, frice, and quadrice. All of these terms are claimed to represent four times.
Since these terms are yet to be officially announced by the world dictionary, nothing can be confirmed of which of these will lead its way of becoming the next in line of thrice. We are aware of the fact that the term thrice is used very rarely, so such a word having a successor will also have a hard time getting used to, which might be the reason it is not considered a term in the numerical system.
In fact, if you say four times, five times, etc., instead of those terms, it sounds easy to say and even easier for the listener to understand it.
Solved Example Involving the Term “Thrice”
A coin is tossed thrice (three times). Find the probability of getting one head in the three tosses.
Solution
The coin is tossed thrice, which means it is flipped three times in a row. A coin has two sides, heads and tails.
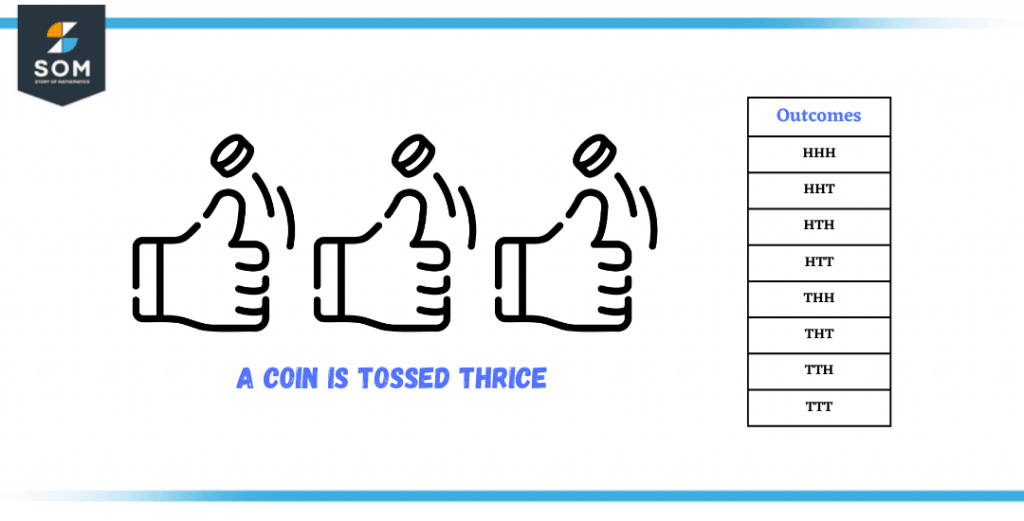
Figure 3 – Example of a coin being tossed thrice
After three tosses, the possible outcomes are:
S = {H,H,H},{H,H,T},{H,T,H},{H,T,T},{T,H,H},{T,H,T},{T,T,H},{T,T,T}
From the above sequence, only once are there no heads in the combination.
And the probability of getting a head is 1/2.
So the total probability of getting at least one head is:
= $\left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right)$
= $\left(\dfrac{1}{2}\right)^3$
= $\dfrac{1}{8}$
So there is one out of 8 times that there would be no head, so subtracting it from 1 gives:
= $\dfrac{(8-1)}{8}$
= $\dfrac{7}{8}$
Thus the probability of getting a head at least once is $\dfrac{7}{8}$.
All images are created using GeoGebra.
