JUMP TO TOPIC
Transformation|Definition & Meaning
Definition
In geometry, a transformation is when we manipulate or change a shape by either rotating(Turning), flipping, translating (sliding), or rescaling it. It is possible to denote these in the form of equations involving the object’s coordinates. Note that transformations are not limited to the field of geometry and extend to several other basic and advanced branches of mathematics.

Figure 1 – Rotation and Reflection Transformation
A new perspective on geometry was introduced in the 19th century by Felix Klein, called transformational geometry. Through the use of transformations, any image in a coordinate plane can be altered. By applying the principles of transformations to video games, we can better understand their graphics.It is important to know how to identify the transformations, understand the rules that govern the transformations of functions, and examine the different types of transformations that we may encounter.
Transformations in Maths
Transformations are functions that map to themselves, i.e., f: X → X. An image X is formed by transforming the pre-image X. As part of this transformation, you can perform any or a combination of operations such as dilation, rotation, reflection, and translation.
In translation, a function is moved along a specific direction, in rotation, a function is rotated around a point, in reflection, the function is reflected in its mirror image, and in dilation, the function is scaled. The concept of transformation in Math explains how two-dimensional figures are moved around a coordinate plane as they rotate.
What are the Different Types of Transformations?
The four most common types of transformation are dilation, translation, rotation, and reflection. If we define a transformation as rotation about a point, reflection over a line, and translation along a vector, we can rotate about any point, reflect over any line, and translate along any vector.
The images in these cases are rigid transformations where the pre-image is congruent to the image. This type of transformation is also called an isometric transformation. Dilation is non-isometric and can take place at any point. In this case, the image is the same as its pre-image.
| Transformation | Function | Result |
| Rotation | A pre-image is rotated or turned around an axis | Size and shape remain the same |
| Reflection | Produces a mirror image by flipping the pre-image | Size, shape, or orientation remain the same |
| Translation | Moves or slides the pre-image. | Size and shape remain the same. Only a change in direction |
| Dilation | Stretches or shrinks pre-images | This function allows you to expand or contract the shape |
Transformation Rules
Suppose we have a function f(x). When you use a coordinate grid, you can measure the movement by using the x-axis and y-axis. Following are some rules that can be applied to the graph of functions for transformations of functions.
The representation of transformations can be either algebraic or graphic. Algebraic functions often involve transformations. It is possible to obtain a graph by applying the formula of the transformation in graphical functions, and by doing so we can move the graph around rather than tabulating the coordinate values of the plot to obtain the graph by transforming the basic or parent function.
Algebraic equations are visualized and learned more easily with the help of transformations.
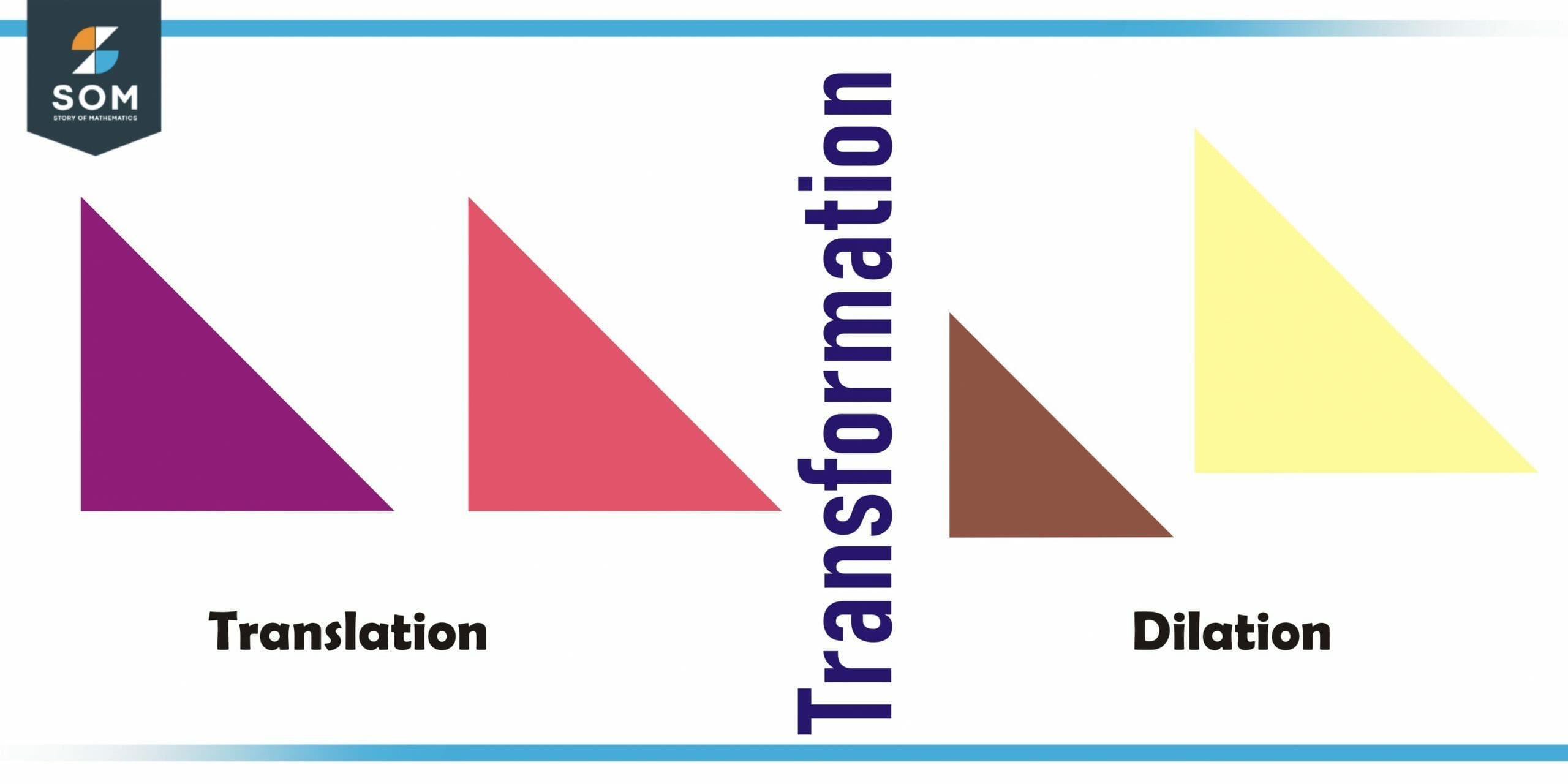
Figure 2 – Translation and Dilation Transformation
Translation Transformation
Two–dimensional shapes slide when they are translated. Translations move shapes up, down, or sideways without changing their appearance. As a result of the translations, the shape is created by a series of points which are all translated in the same distance and the same direction at each point.
How to Describe Translations
Translations are described in terms of column vectors. For example (2/-4), this means that translate the shape 2 squares to the right and 3 squares down. (-4/3) this means that translate the shape 4 squares to the left and 3 squares to the up.
In vectors (a/b) a represents horizontal movement, and b represents vertical movement. A positive value of a indicates a rightward movement, while a negative value of b indicates a leftward movement. When b is positive, the movement is upward, and when b is negative, the movement is downward.
Reflection Transformation
The axis of reflection or line of reflection flips all the points of an object. Whenever an image is reflected, it retains the same shape and size as the original. Transformations of this type are known as isometric transformations. They are facing opposite directions, which means they are laterally inverted.
Coordination Plane Reflection
Let’s examine how the coordinate plane reflects points and shapes. When the points are reflected over different lines of reflection, it will be helpful to note the pattern of the coordinates.
- The image of (a, b) is the point (a, -b) if it is reflected on the x-axis
- The image of (a, b) is the point (-a, b) if it is reflected on the y-axis
- The image of (a, b) is the point (b, a) if its reflection is on the line y = x.
- An image of (a, b) can be found at the point (-b, a) if it is reflected on the line y = -x.
The Geometry Reflection
An image and its original are congruent when a reflection occurs, which is usually referred to as a flip. Performing a geometry reflection requires a line of reflection; the figures are oriented in opposite directions.
Rotation Transformation
When an object is rotated about a fixed point, it is considered a transformation. Rotation is either in a clockwise manner or anti-clockwise. The center of rotation is a fixed point at which rotation occurs. It is the angle of rotation that determines how much rotation is made.
Dilation Transformation
A dilation is a form of transformation that involves resizing an object by altering its size. As a result of dilation, the objects can be made larger or smaller in size. “Scale factor” is the term used to describe this transformation.
- It is known as enlargement when a dilation results in a larger image.
- Reduction occurs when a dilation produces a smaller image.
An Example of a Reflection
It is possible to combine transformations of shapes, as there are five different types. Reflection and translation of a polygon produce an image that appears apart from its preimage and is mirrored. By enlarging and shearing a rectangle, it appears as a larger parallelogram.
The point (-3, 2) Where is the point now if it is reflected over the x-axis?
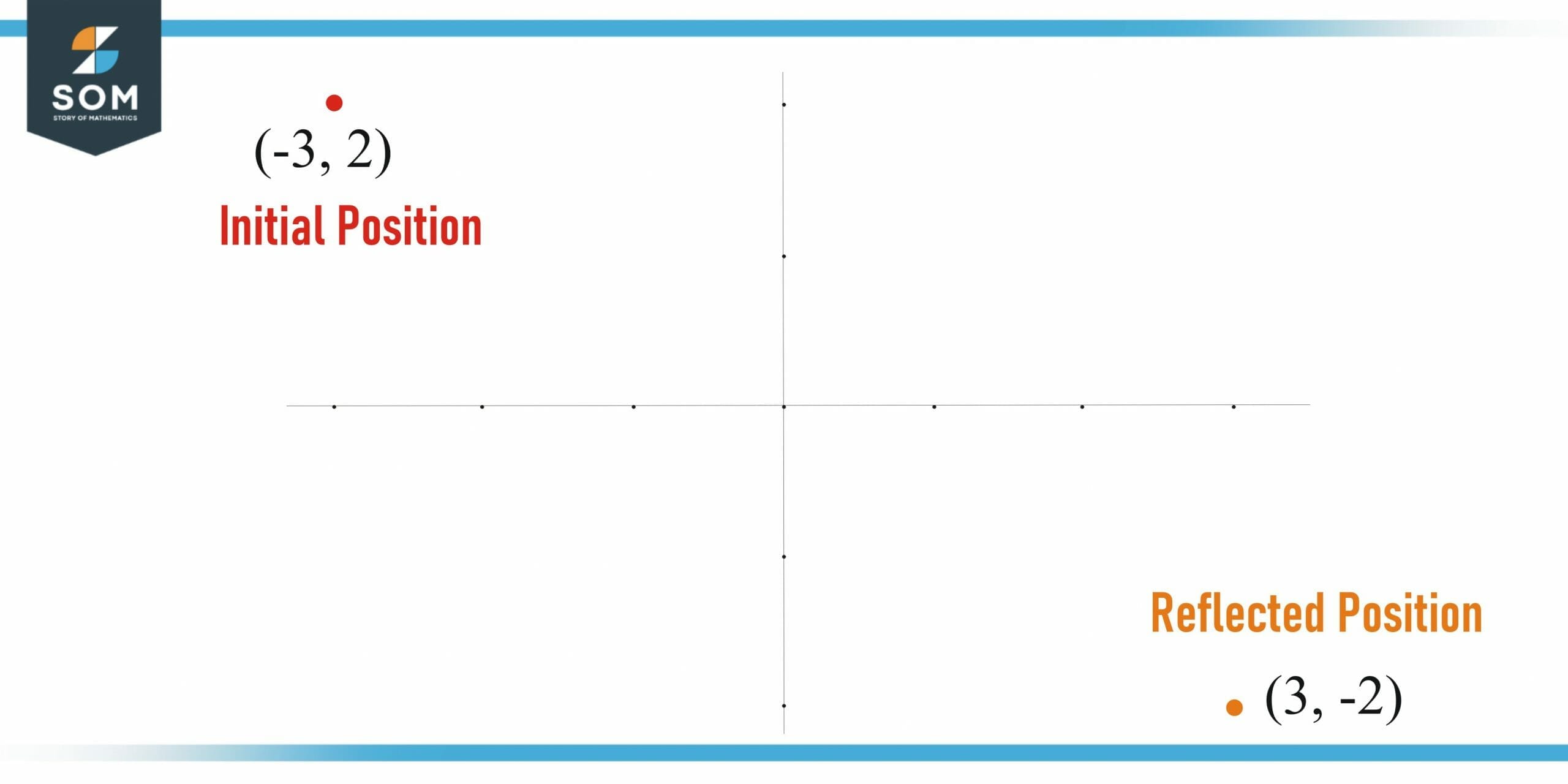
Figure 3 – Reflection of a point
Solution
As in reflection, (x, y) = (x, -y), so the point (-3, 2) will be (3, -2) after reflection.
All images were created with GeoGebra.
