Transpose (Matrix)|Definition & Meaning

One of the most used methods in linear algebra is the transpose of a matrix. This method can be achieved by interchanging the rows with the columns and each column with the rows of the given matrix. In other words, flipping a matrix over its diagonals will carry out the transposition of that matrix.

Before going into detail about the transpose of a matrix, let’s first learn the basic concepts of a matrix. 

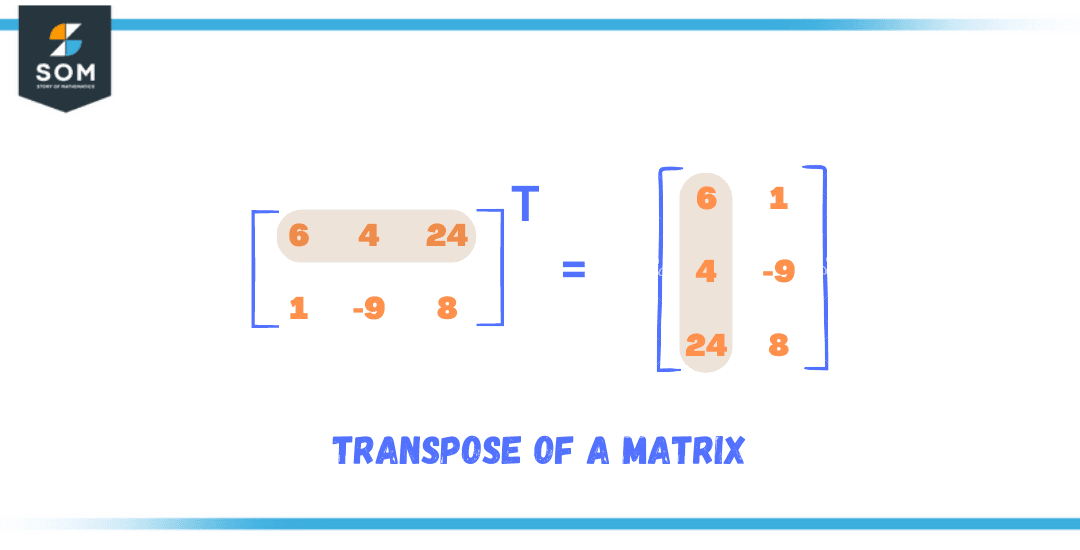
Figure 1 – Transpose of a Matrix

What Is a Matrix?

A matrix is a modified form of a table with rows and columns of numerical data or mathematical functions arranged in rectangular arrays. Since the number of rows and columns can vary, the matrices are divided into many types. The simplest form of a matrix contains one row and one column:

$\begin{bmatrix} 1 \end{bmatrix}$

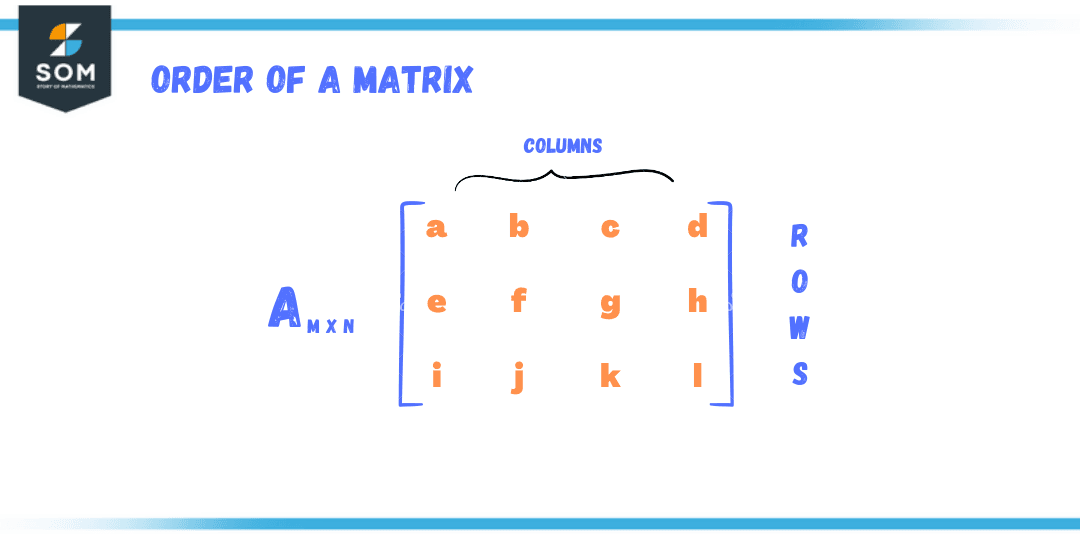
Figure 2 – Order of a Matrix A

In practical mathematics, matrices have multiple rows and columns, like the one given below:

A = $\begin{bmatrix} 1 & 2 \\ a & b \\ x & y \end{bmatrix}_{3\times 2}$

In the above matrix, there are a total of 3 rows and 2 columns. This defines the order of a matrix, i.e., 3 x 2. Thus the total number of elements is 6.

A row is defined by the horizontal array, whereas the vertical array is comprehended as the column.

Let’s take a look at another form of a matrix:

B = $\begin{bmatrix} 1 & 2 & 3\\ a & b & c \end{bmatrix}_{2\times 3}$

As you can see, there is a visual difference in both matrices A and B, as there are a greater number of rows in matrix A than in matrix B. Such a matrix having more rows than columns is known as a vertical matrix, whereas matrix B has a greater number of columns than A, which makes it a horizontal matrix.

Let’s suppose we have a situation in which every element of matrix A is present in matrix B, and both have the same number of elements. Then are these matrices equivalent? To answer this question, a formula has been provided, which is stated as:

A = $\begin{pmatrix} a_{ij} \end{pmatrix}_{m\times n}$ and B = $\begin{pmatrix} b_{ij} \end{pmatrix}_{r\times s}$

For A and B to be equivalent, the following points have to be considered,

• m = r and n = s such that the order must be the same for the two matrices.
• For $a_{ij} = b_{ij}$, every value of i and j must be equal.

What Is the Transpose of a Matrix?

In matrix nomenclature, transpose is a procedure that switches the horizontal and vertical arrays of a matrix. This feels like reversing a matrix over its diagonal. It is characterized using a tick or a capital superscript “T” after the matrix or its title, e.g., A’ or A$^T$ where A is any matrix.

The general form of a transposition goes by this statement:

If A = $\begin{pmatrix} a_{ij} \end{pmatrix}_{m\times n}$ then A’ = $\begin{pmatrix} a_{ij} \end{pmatrix}_{n\times m}$

Thus a transpose of a matrix can also be stated as a method of converting all the rows into the corresponding columns of a given matrix and vice-versa.

How To Find the Transpose of a Matrix?

Interchange the rows and columns sound quite straightforward, but that’s not it. Let’s say we have a matrix of order 2×3 which means that it contains 2 rows and 3 columns, and the total number of elements is 6.

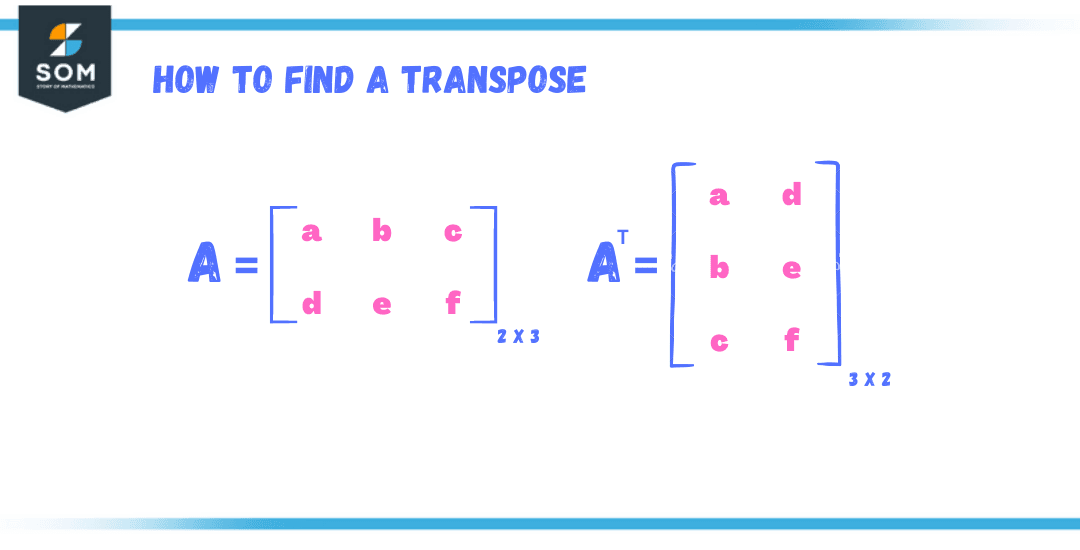
Figure 3 – How to find the transpose of a Matrix

The process of the transpose of a matrix starts by taking the first row and sliding it onto the first column of a new matrix. The new matrix will thus contain one column with all the row elements of the previous matrix.

Similarly, the second row of the given matrix will be mapped as the second column of the new matrix, with all the elements remaining the same.  Thus the new matrix now has a total of 3 rows and 2 columns, defining a new order 3×2 for the new matrix.

Properties of a Matrix Transpose

The properties of matrix transpose can be better understood by taking two matrices of equal order. Let those matrices be A and B; then their transpose properties can be defined as follows,

Double Transpose

Double transpose means taking the transpose of a transposed matrix. This results in a matrix that is exactly equal to the original one. Such as, the transpose of matrix A is A’, and the transpose of A’  will be (A’)’, which is equal to matrix A.

The concept behind this property is that every element of A that is $a_{ij}$ gets flipped to $a_{ji}$ when the first transpose is taken. Thus making A’. Now, if another transpose is taken, the element $a_{ij}$ gets flipped back to $a_{ij}$, which was the element of the original matrix A.

Let’s say we have a matrix Z:

Z = $\begin{bmatrix} 20 & 12 & 6\\ 9 & 7 & 0 \\ 3 & 89 & 20 \end{bmatrix}$

Then:

Z’ = $\begin{bmatrix} 20 & 9 & 3\\ 12 & 7 & 89 \\ 6 & 0 & 20 \end{bmatrix}$

And:

(Z’)’ = $\begin{bmatrix} 20 & 12 & 6\\ 9 & 7 & 0 \\ 3 & 89 & 20 \end{bmatrix}$ = Z

Addition of Transposed Matrices

Adding two individually transposed matrices is the same as adding the matrices and then taking the transpose of their sum. It is more like a distributive property of matrices.

To prove that (A + B)’ = A’ + B’, let’s say we have two matrices, A and B:

A = $\begin{bmatrix} 2 & -3 & 8\\ 21 & 6 & -6 \\ 4 & -33 & 19 \end{bmatrix}$ and B =  $\begin{bmatrix} 1 & -29 & -8\\ 2 & 0  & 3 \\ 17 & 15 & 4 \end{bmatrix}$

Then:

A + B = A = $\begin{bmatrix} 2 & -3 & 8\\ 21 & 6 & -6 \\ 4 & -33 & 19 \end{bmatrix}$ + B =  $\begin{bmatrix} 1 & -29 & -8\\ 2 & 0  & 3 \\ 17 & 15 & 4 \end{bmatrix}$ = $\begin{bmatrix} 3 & -32 & 0\\ 23 & 6 & -3 \\ 21 & -18 & 23\end{bmatrix}$

(A + B)’ = $\begin{bmatrix} 3 & 23 & 21 \\ -32 & 6 & -18 \\ 0 & -3 & 23\end{bmatrix}$

Now:

A’ + B’ = $\begin{bmatrix} 2 & 21 & 4 \\ -3 & 6 & -33  \\ 8 & -6 & 19 \end{bmatrix} +  \begin{bmatrix} 1 & 2 & 17 \\ -29 & 0 & 15  \\ -8 & 3 & 4 \end{bmatrix} = \begin{bmatrix} 3 & 23 & 21 \\ -32 & 6 & -18  \\ 0 & -3 & 23 \end{bmatrix}$

Thus Proved that (A + B)’ = A’ + B’.

Multiplying a Constant

It is the same as the addition of transposed matrices, meaning that if a constant is multiplied by a matrix and then the transpose is taken, this will be equal to multiplying the constant with the transposed matrix as:

(kA)’ = kA’

Multiplication Property

Multiplying two matrices and then taking their transpose is equal to multiplying two transposed matrices but in reverse order such as:

(AB)’ = B’A’

Solved Example of Transpose of a Matrix

For the given matrices A and B, prove that (AB)’ = B’A’.

A = $\begin{bmatrix} 9 & 8 \\ 2 & -3 \end{bmatrix}$ and B = $\begin{bmatrix} 4 & 2 \\ 1 & 0 \end{bmatrix}$

Solution

First, we will find the left-hand side:

A $\times$ B = $\begin{bmatrix} 44 & 18 \\ 5 & 4 \end{bmatrix}$ $\Rightarrow$ (AB)’ = $\begin{bmatrix} 44 & 5 \\ 18 & 4 \end{bmatrix}$

B’A’ = $\begin{bmatrix} 4 & 1 \\ 2 & 0 \end{bmatrix} \begin{bmatrix} 9 & 2 \\ 8 & -3 \end{bmatrix}$

= $\begin{bmatrix} 44 & 5 \\ 18 & 4 \end{bmatrix}$ = (AB)’

Therefore, (AB)’ = B’A’.

A’B’ =$\begin{bmatrix} 9 & 2 \\ 8 & -3 \end{bmatrix} \begin{bmatrix} 4 & 1 \\ 2 & 0 \end{bmatrix} = \begin{bmatrix} 40 & 9 \\ 26 & 8 \end{bmatrix}$

This shows that (AB)’ $\ne$ A’B’.

All images are created using GeoGebra.

Transformation Definition < Glossary Index > Transversal Definition