Transversal|Definition & Meaning

What Is a Transversal?

In the field of geometry, a transversal line is a line that travels through two other lines within the same plane at two different points. In the Euclidean plane,  transversals are an essential component in the process of producing parallelism between two or more additional straight lines. It meets two lines at different spots where they overlap. The intersection that results from the Transversal creates several angles. These are called corresponding angles, co-interior angles, alternative interior angles, and alternate exterior angles.

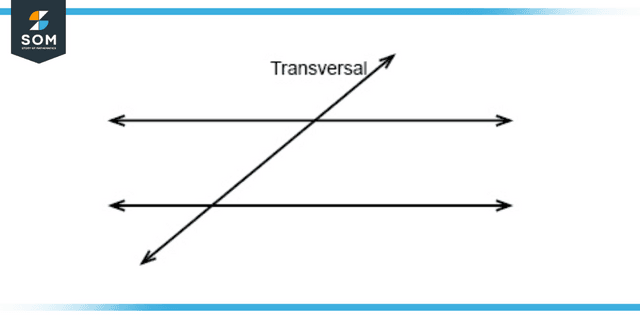
Figure 1: Representation of transversal line.

Transversal and Transversal lines

In the field of mathematics, a transversal is any line that, at distinct locations, intersects two other straight lines. In the following diagram, the line labeled “L” is a transversal line that crosses the lines labeled “L1” and “L2” at two separate locations. Within the realm of lines that are parallel and lines that are transverse, a transversal line is what joins two parallel lines.

Transversal Angles

A transversal creates several different angles, including sides and angles, exterior angles of inclination, pairs of points of intersection, pairs of alternate interior angles, pairs of alternate exterior angles, and the pair of interior angles that are on the same side of the Transversal. Each of these angles can be further broken down into additional subtypes. Every one of these angles can be determined in either scenario, which can refer to lines that are parallel or not parallel.

Angles Formed by Parallel Lines and Transversals

When lines or transversal cuts over two parallel lines, the angles created as a result have the same measure. Therefore, the angles produced by the first line intersecting the transversal produce angles equivalent to their corresponding angles produced by the second line intersecting the Transversal.

Angles Formed by Non-Parallel Lines and Transversals

If a transversal intersects two lines that are not parallel, the resulting angles have no connection to one another, even though they are both the result of the same event. They are not identical to one another, as is the case with parallel lines, but they all correspond to one another. In the same way, there is no connection between the interior, exterior, laterally opposing, and successive angles when a transversal cuts over the intersection of two lines that are not parallel to one another.

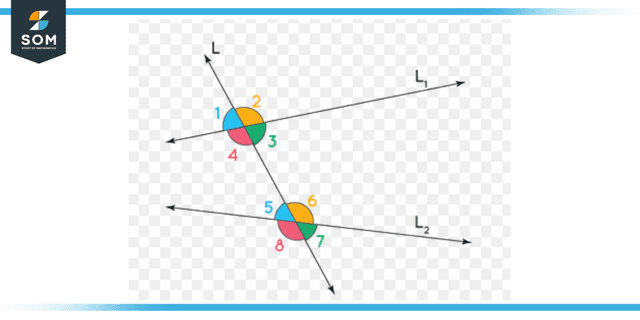
Figure 2: Representation of angles formed by non-parallel lines.

Alternate Interior and Exterior Angles

The angles produced when a transversal crosses two coplanar lines are alternate interior angles. They are on the exact same side of the parallel lines as the parallel lines. However, they are on opposing sides of the Transversal.

The Transversal cuts it through two coplanar lines at two different places, then continues on to the third point. The values of these angles indicate whether or not the two lines presented here are parallel to one another. If these angles are the same as one another, then the lines that the Transversal cuts through will parallel.

Alternate external angles are the pair of angles produced on the exterior side of the parallel lines and the opposite side of the Transversal. These angles can only be generated when the parallel lines and Transversal are drawn in opposing directions.

Properties of Transversal

The following characteristics can be specified whenever the intersection of two parallel lines produces a transversal.

• The measure of each angle formed by a pair of similar angles is the same for each Transversal that cuts two parallel lines.
• When a transversal cuts 2 parallel lines, the inner angles of each pair of alternating lines are the same.
• Each combination of interior angles situated on the same side of a transversal is considered supplemental if a transversal intersects two parallel lines.

Transversal Theorem

Several theorems, including the following, have been defined for Transversal:

• If a transversal cuts through two parallel lines, then the angle formed by each matching pair of those lines is the same.
• Two lines are considered parallel if a transversal cuts across them in such a way that a pair of angles formed by the intersection are proportional to one another.
• Two lines are considered parallel if a transversal cuts through them so that a pair of alternate interior angles are proportional to one another.
• A transversal is said to have supplemental interior angles for any pair of internal angles that are on the exact same side of the Transversal when it meets two parallel lines.

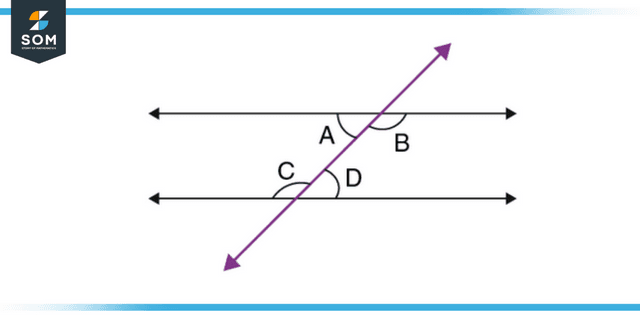
Figure 3: Representation of supplemental interior angles.

How Exactly Can One Recognize a Transversal?

Because it crosses two or more lines at different points, the Transversal is easy to spot and identify.

What Is the Graphic Representation of Transversal?

In mathematics, there is no one particular symbol that may be used to represent a transversal.

How Do You Label a Transversal?

A transversal can be labeled the same way as other lines in geometry, which means we can use the alphabet. For instance, line PQ represents the Transversal of lines AB and CD.

Examples of Transversal

Example 1

Three archers shot arrows that hit a tree. Arrow X and arrow Y are parallel to the ground, and arrow Z goes across the other two arrows. If arrows X and Y make a larger angle of 140°, then at what angle the third archer launched arrow Z?

Solution

Let’s consider the angle that arrow Z is making is A then,

140° + A = 180°

A = 180° – 140°

A = 40°

Example 2

Consider a transverse intersecting two parallel lines, A and B. The point where it intersects line A is at an angle of 75°, and the point where it intersects point B is unknown. Determine the angle at which the transverse is intersecting point B.

Solution

Finding the angle by using the property of parallel lines cutting by a transversal. Using alternate interior angle property to find the unknown angle.

B + 75° = 180°

B = 180° – 75°

B = 105°

All images/graphs are created using GeoGebra.

Transpose Matrix Definition < Glossary Index > Trapezium Definition