Trapezium|Definition & Meaning

What Is Trapezium?

A trapezium is a quadrilateral with convex sides and one pair of parallel sides. If you were to draw a trapezium on a flat piece of paper, it would look like a table. A quadrilateral is a four-sided polygon with four corners according to Euclidean geometry. Since there are four sides, four angles, and four vertices in a trapezoid, the trapezium has the same properties.  

The trapezium shape is ubiquitous in nature and architecture. The trapezium rule extensively uses trapezoids by dividing the area under a curve into a set number of trapezoids and then evaluating the area of each trapezoid.

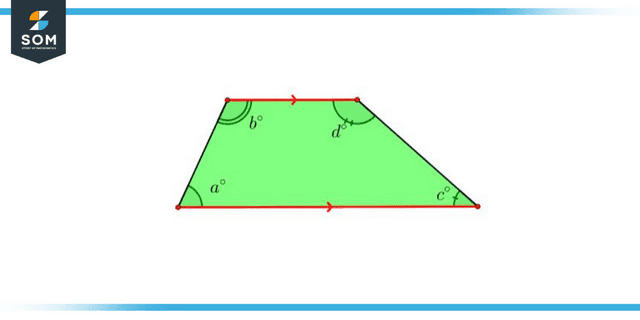
Figure 1: Allied Angle of Trapezium

The Shape of a Trapezium

As a quadrilateral, the trapezium has one set of parallel sides. Trapeziums have bases for their parallel sides and legs for their non-parallel sides. You may also hear this shape referred to as a trapezoid. The parallelogram is a trapezoid with parallel sides.

Types of Trapezium

There are three basic type of the trapezium:

1. The isosceles trapezium
2. Right Trapezium
3. Scalene

The Isosceles Trapezium

It is referred to as an isosceles trapezium when either the legs of the trapezium or the unparallel sides are of the same length.

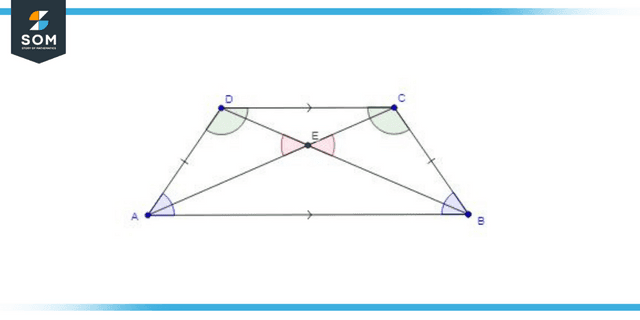
Figure 2: Isosceles Trapezium

Right Trapezium

A trapezium is considered right (or correct) when it has at least two right angles close to one another.

Scalene Trapezium

The term “scalene trapezium” refers to a trapezium in which each side and angle is of a distinct measurement.

Irregular Trapezium

As is common knowledge, a trapezium accurately has one set of parallel sides, whereas the remaining two do not share a parallel relationship. Now, the other two non-parallel sides of a regular trapezium will be equal, whereas the other two non-parallel opposing sides of an irregular trapezium will not be equal.

Characteristics of the Trapezium

The following is a list of significant characteristics that a trapezium possesses:

1. Only one pair of the trapezium’s opposite sides are parallel at any given time.
2. The diagonals cross over one another.
3. The parallel sides of the trapezium are only equal to each other, except for the isosceles trapezium.
4. The line that unites the midpoints of the sides that are not parallel is also always parallel to the base or the sides that are parallel, and its length is equal to half of the total length of the sides.
5. The legs or sides that are not parallel in an isosceles trapezium are congruent.
6. The whole amount of the trapezium’s inner angles added together equals 360 degrees. e., ∠A + ∠B + ∠C + ∠D = 360°
7. The combined degrees of the two nearby angles add up to 180 degrees. This indicates that the two angles that are adjacent to one another are complementary.

Area of Trapezium

You may calculate the area of a trapezium by calculating the average of both bases of the trapezium and multiplying that number by the height of the trapezium. Therefore, the formula for the area of the trapezium is as follows:

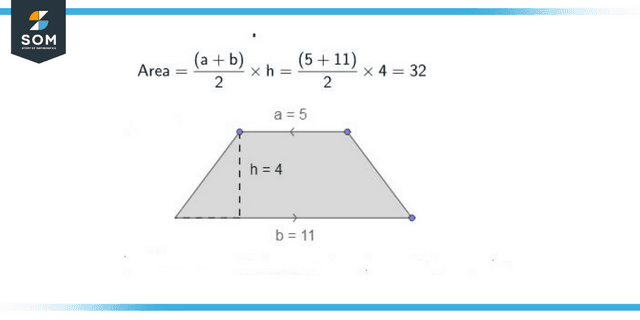
Figure 3: Area of Trapezium

We can calculate the area of a trapezium as follows:

A = [h (a + b) / 2] square units

Where the foundations are “a” and “b,” and “h” denotes the altitude, also known as height.

Length of the Trapezium’s Perimeter

To calculate the trapezium’s perimeter, sum up all the side lengths. As a result, the formula for determining the perimeter of a trapezium is as follows:

P is the trapezium’s perimeter = a+ b + c + d

Where,

The edges of the trapezium are labeled “a,” “b,” “c,” and “d,” respectively.

Trapezium and Trapezoid

The trapezium is a polygon with four sides and a two-dimensional shape with precisely one set of parallel sides perpendicular to each other.

In addition to having four sides, a trapezoid has one pair of parallel sides that run in the opposite direction from one another. The two sides parallel to one another are known as the bases, while the other two are referred to as the legs.

Even though the meanings of both words might vary depending on the country, both are equivalent in general mathematics.

How To Calculate the Angles of a Trapezoid?

In a regular or isosceles trapezium, the sets of angles enclosed by line segments are all the same size. Additionally, we know that the total of any quadrilateral’s internal angles is always equal to 360 degrees.

Therefore, if an angle, let’s call it x, is given between one side that is parallel and another side that is not parallel, then taking double this angle and subtracting it from 360 will produce the sum of two angles that are generated on the side that is opposite x. After the sum has been computed, the measurement of the last angle can be obtained by dividing it by two and taking the result.

Solved Problems With Trapezoids

Example 1

Find the parameter of a trapezium with sides; 7 cm, 6 cm, 2 cm, and 2 cm.

Solution

The parameter of a trapezium is the sum of all the sides of the respective shape. Therefore, the answer is as follows:

P = a + b + c + d

P = 7 + 6 + 2 + 2

P = 17 cm

Example 2

An isosceles trapezium has a perimeter of 48 cm, where the sides are two times greater than one another. Find the dimensions of the shape.

Solution

P = a + b + c + d

Here:

b = d

a = 2.c

c = 4

Insert values into the formula:

P = (2.c) + d + 4 + d

48 = 8 + 2d + 4

2d = 36

d = 18 cm

Thus, b = d = 18 cm, a = 8 cm, and c = 4 cm.

If all the dimensions are added up, the answer matches the left side of the equation, i.e., 18 + 18 + 8 + 4 = 48 cm.

All mathematical drawings and images were created with GeoGebra.

Transversal Definition < Glossary Index > Tree Definition