JUMP TO TOPIC
Undecagon|Definition & Meaning
Definition
An undecagon is an 11-sided polygon referred to as a hendecagon or an undecagon. Regular undecagons have all sides the same length and vertices that are evenly placed around a circle.
Visualizing an Undecagon
Undecagon has 11 sides and 11 angles, all of the sides and angles are equal. It also has 11 vertices.
Figure 1 below shows an 11-sided polygon ABCDEFGHIJK. This 11-sided polygon is an undecagon.
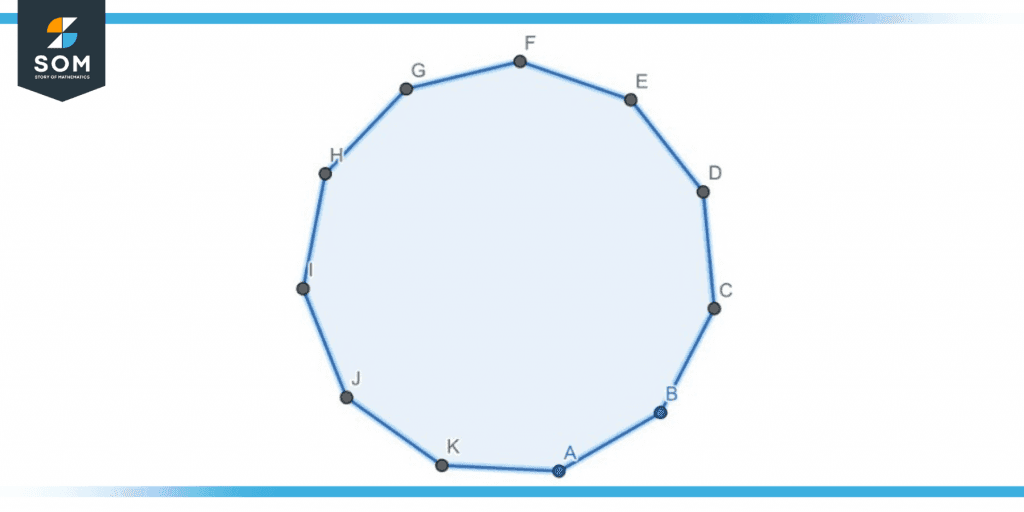
Figure 1 – Diagram of an undecagon.
What Is a Polygon?
A polygon is a geometric object with two dimensions and a finite number of sides. A polygon’s sides are made up of segments of straight lines that are joined endlessly. As a result, a polygon’s line segments are referred to as its sides or edges.
Vertex or corners refer to the intersection of two line segments when an angle is created. Having three sides makes a triangle a polygon. A circle is a planar figure but isn’t considered a polygon because it’s curved and lacks sides and angles. So, while all polygons are two-dimensional forms, not all two-dimensional figures are polygons.
A minimum of three line segments must be connected end to end to create a closed figure. As a result, a polygon having at least three sides is known as a triangle and is also known as a 3-gon. An n-gon is a polygon with n sides.
The following Figure shows a polygon:
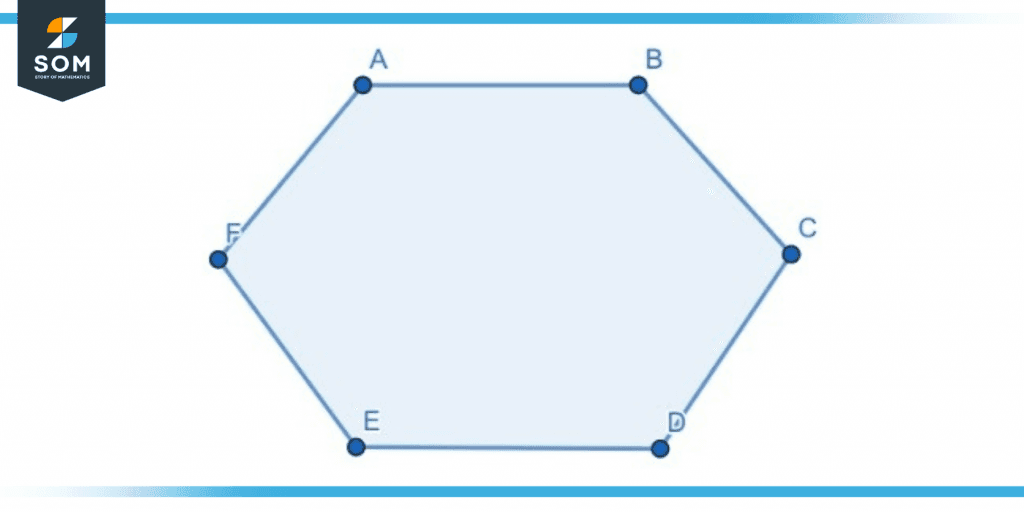
Figure 2 – Representation of a regular polygon.
Characteristics of Regular Undecagon
Below are some characteristics of a regular undecagon.
- Interior angle:
An undecagon has an interior angle of 147°. The formula $\frac{180n-360}{n}$ is used to determine the interior angle of a regular polygon, n=11, for an undecagon. You can look at the interior angles in Figure 3. - Exterior angle:
The outer angle of an undecagon is 33°. Because it is the case that the exterior angle and interior angle constitute a linear pair, we may use the formula 180-interior angle to get the exterior angle of a normal undecagon. You can see the exterior angle in Figure 3. - Area:
The approximate area of an undecagon is $9.365s^{2}$, in which S is the length of a side. There are several ways to determine the precise area of an undecagon or any other polygon. - The number of diagonals in an undecagon:
Forty-four diagonals make up an undecagon. The total number of unique diagonals that may be formed from all vertices. We calculate the number of diagonals by the formula: Diagonal = $\frac{1}{2n(n-3)}$. - Number of Triangles:
Nine triangles make up an undecagon. The number of triangles formed when the diagonals are drawn from a specific vertex. We can find the number of triangles in an undecagon by using the formula n-25. - Sum of Interior Angles:
The sum of interior angles in an undecagon is 1620°. This can be found using the formula: Interior Angle = 180(n-2) - Hendecagonal Prism:
In this instance, the hendecagonal prism is convex in geometry, created by cubic sides, two regular polygonal tops, and two undecagons. Thus, it has 11 squares and two undecagons as its faces. Eleven rectangular sides and two hendecagonal bases make up the hendecagonal prism.
The following figure 3 displays the interior and exterior angles of a regular undecagon:
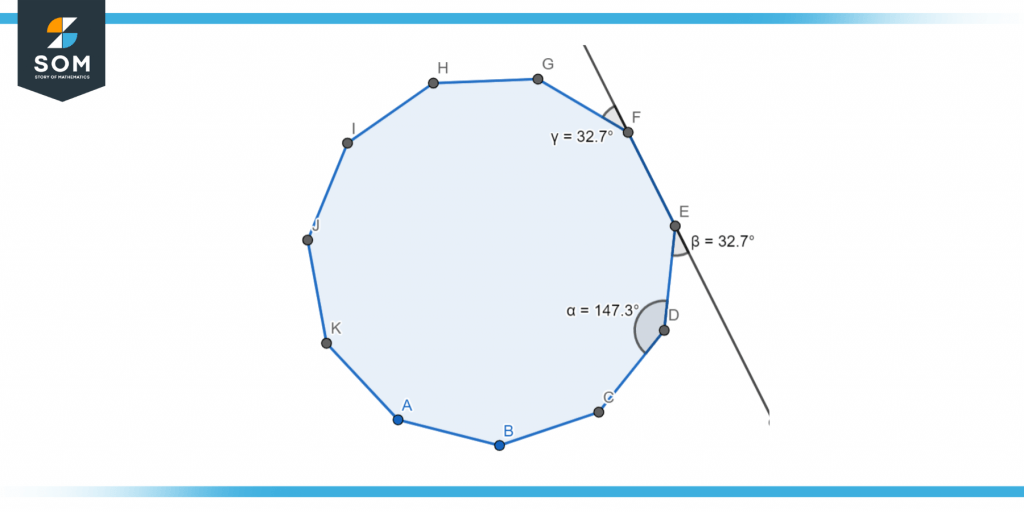
Figure 3 – Diagram showing the interior and exterior angles of an undecagon.
Perimeter and Area of Undecagon
Perimeter of Undecagon
The perimeter of a form is the space surrounding its edge. Find the perimeter of various forms by summing the lengths of their sides. The perimeter of the undecagon is Perimeter = 11 x sides.
Area of Undecagon
The area is the entire space occupied by a flat (2-D) surface or an object’s form. On a sheet of paper, draw a square using a pencil. It has two dimensions. The area of a form on paper is the area that it occupies.
The area of an undecagon can be found using the formula A = side x side x 9.336.
How Is Undecagon Used in Coinage?
Along with the Indian 2-rupee currency and several other less common coins from other countries, the Canadian dollar coin, known as the loonie, resembles but is not a replica of a standard hendecagonal prism. In reality, a loonie’s cross-section is a Reuleaux hendecagon.
Over the years, other commemorative and specimen-set editions of the coin have been produced, each featuring a unique design in place of the loon on the reverse. The coin has an 11-sided Reuleaux polygonal shape. Its 11 sides and 26.5 mm diameter matched those of the Susan B, which was already in circulation.
Examples of Undecagon
Here are a few solved examples of an undecagon to understand, which would help you further understand the concept.
Example 1
A regular undecagon marked in a circle has a side length of 8 meters; calculate the perimeter and the area of the circle in which it is marked.
Solution
It requires the perimeter P:
Side Length = 8m
We can get the result by the formula: P = 11 x sides. When we put the values in the formula, we get:
P = 11 x 8m = 88m
Now to find the area of the undecagon, we use the formula: A = side x side x 9.366. After putting in all the values, we get the area as A = 599.424$m^{2}$
Example 2
Calculate the area of a regular undecagon, knowing that the side is 20 cm and the inclination measures 34.8cm.
Solution
It requires the area of an undecagon regular whose sides are:
Length of a side = 20 cm
To calculate the area apply the formula A = side x side x 9.366. After inputting the values in the equation, we get the area as A = 3746.4 $cm^{2}$
Example 3
Calculate the area and perimeter of a regular undecagon having a length of sides of 5cm.
Solution
We can find the perimeter quickly using the formula P = 11 x sides. The perimeter we get is P = 5 x 11 = 55cm. Now to find the area, we use the formula A = side x side x 9.366.
We input the values in the formula and get the area of the undecagon as A = 234.15$cm^{2}$.
All images/tables are made using GeoGebra.
