Unary Operation|Definition & Meaning

Unary operations in mathematics are the type of operations that have only one input and one output. In other words, such operators just transform a number into another one through some kind of mapping which may be one-to-one or one-to-many. 

Some examples of unary operators include additive or multiplicative inverse, absolute operator, factorial, trigonometric operators, etc. The following figure depicts the basic concept.

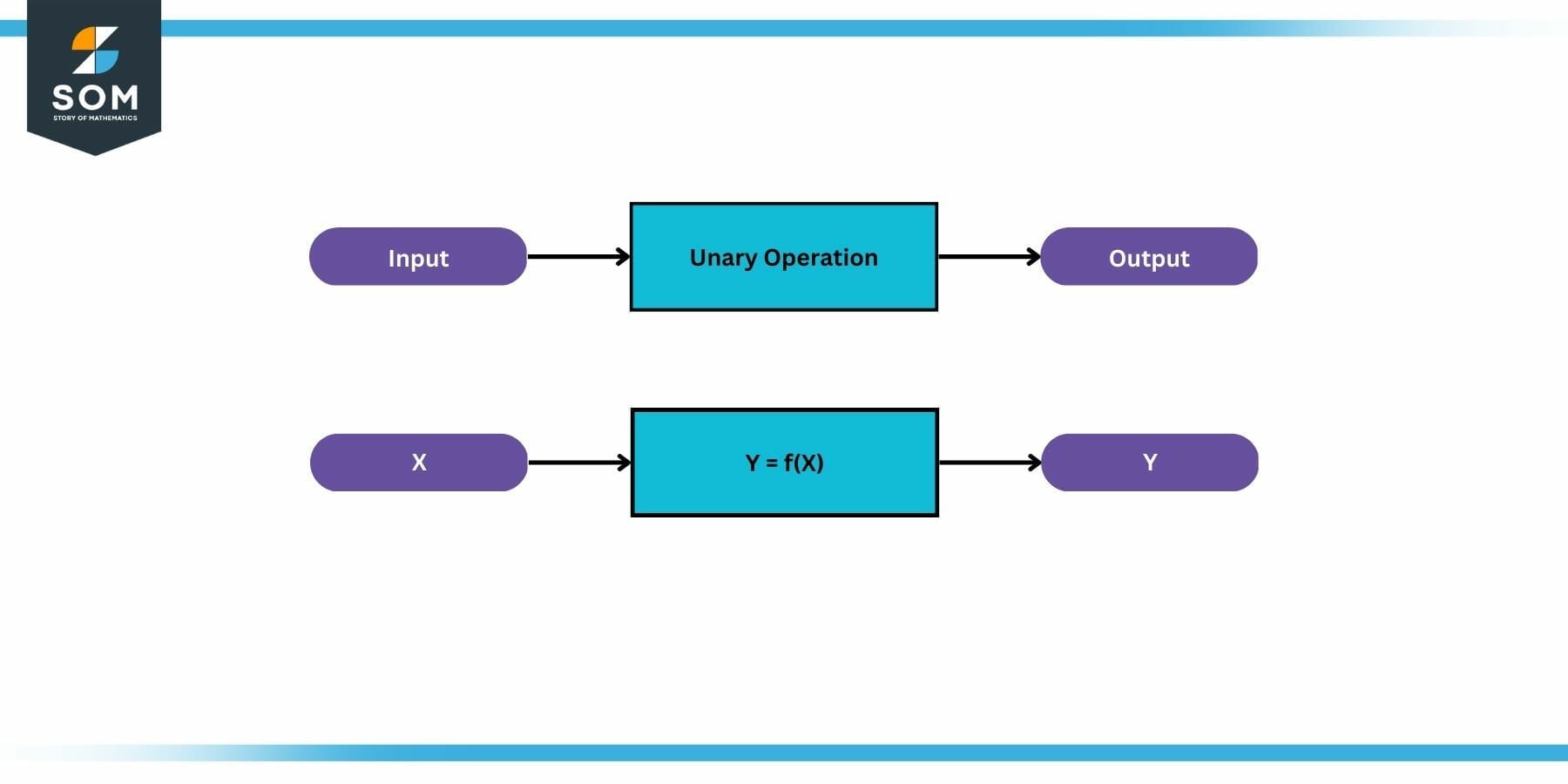
Figure 1: Unary Operation

Explanation of Unary Operation

The concept of unary operation is so simple that it is very self-explanatory. In this article, we will try to develop an understanding of the key concepts related to such operators through examples.

This will not only help us construct an in-depth intuitive foundation but also program our minds for solving unary operation-related problems simultaneously.

There are a lot of unary operations in use in all areas of science, technology, engineering, and mathematics.

For the sake of structure, we have classified them broadly into three categories, namely numeric unary operations, matrix unary operations, and programming unary operations. Some of the most commonly used unary operations are listed below:

1. Numeric Unary Operations

• Absolute Value
• Multiplicative Inverse
• Additive Inverse or Negation
• Trigonometric Operations
• Factorial
• Square Root, Cube Root, etc.
• Square, cube, etc.
• Hyperbolic Operations
• Logarithms

2. Matrix Unary Operations

• Matrix Transpose
• Adjoint of a Matrix
• Determinant of a Matrix
• Inverse of a Matrix

3. Programming Unary Operations

• 1s Complement
• 2s Complement
• Increment
• Decrement
• Logical Negation

Examples of Unary Operations

Now that we have summarized a comprehensive list of unary operations that are commonly used in the field, we can dive deeper into the understanding of these operators through examples. Lets consider them one by one.

1. Numeric Unary Operations

As listed earlier, there are numerous numeric operators. The following diagram shows some of these:

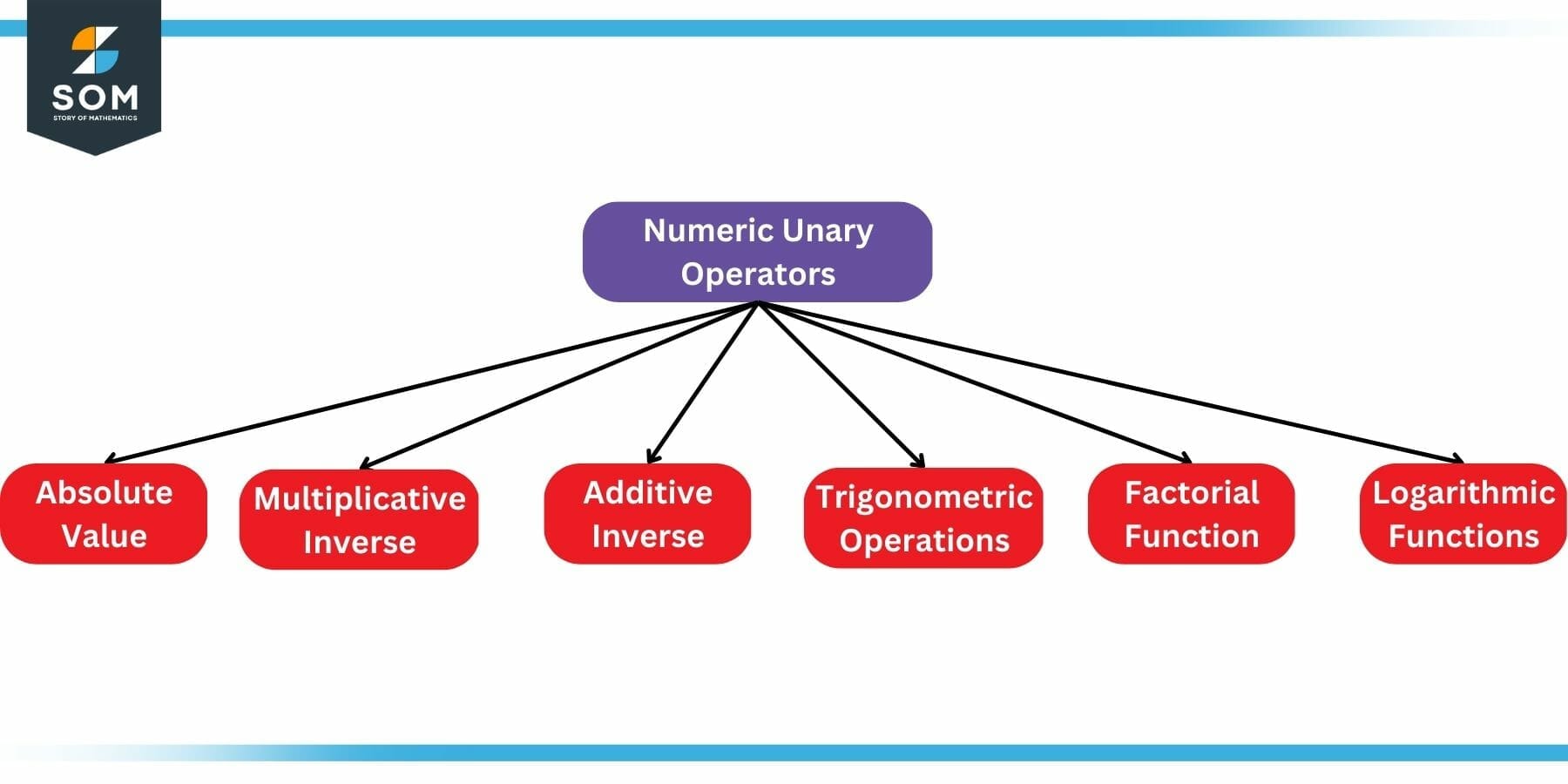
Figure 2: Numeric Unary Operations

(a) Absolute Value: This operator simply removes the negative sign. For example, the absolute value of +10 is +10, and the absolute value of -10 is also +10.

(b) Multiplicative Inverse: This operator is also called a reciprocal operator. It converts the number into its multiplicative inverse. This means that if a number is multiplied by its multiplicative inverse, the result would be 1. For example, the multiplicative inverse of 10 is 1/10, and that of 20 is 1/20.

(c) Additive Inverse or Negation: This operator is also called the negation operator. It converts the number into its additive inverse, meaning that if a number is added into its additive inverse, the result would be 0. For example, the additive inverse of 10 is -10, and that of 20 is -20.

(d) Trigonometric Operations: Trigonometric ratios are most common in geometry. They can be defined as the unary operations on an angle. There are six such ratios by definition, including sine, cosine, tangent, and their inverses, namely secant, co-secant, and co-tangent. They operate on angles only. For example, the sine of 30 degrees is equal to 0.5.

(e) Factorial: Factorial of a positive number is defined as the multiplication of that number with all positive numbers that are smaller than it. For example factorial of the number 4 is equal to 4 x 3 x 2 x 1, which is equal to 24.

(f) Square Root: Square root is a unary operation that calculates such a number that the square of that number returns the original one. For example, the square root of 4 is 2.

(g) Square: Square is a unary operation that returns the multiplication of the number by itself. For example, the square of 2 is equal to 2×2, which equals 4.

(h) Logarithms: Logarithms are used in solving exponents. They are defined as the exponent that raises a base to achieve the input number. For example, the logarithm of 100 on base 10 equals 2. This means that 10, raised to the power of 2, will result in 100.

2. Matrix Unary Operations

Matrices have their own set of unary operations. The following figure summarizes them:

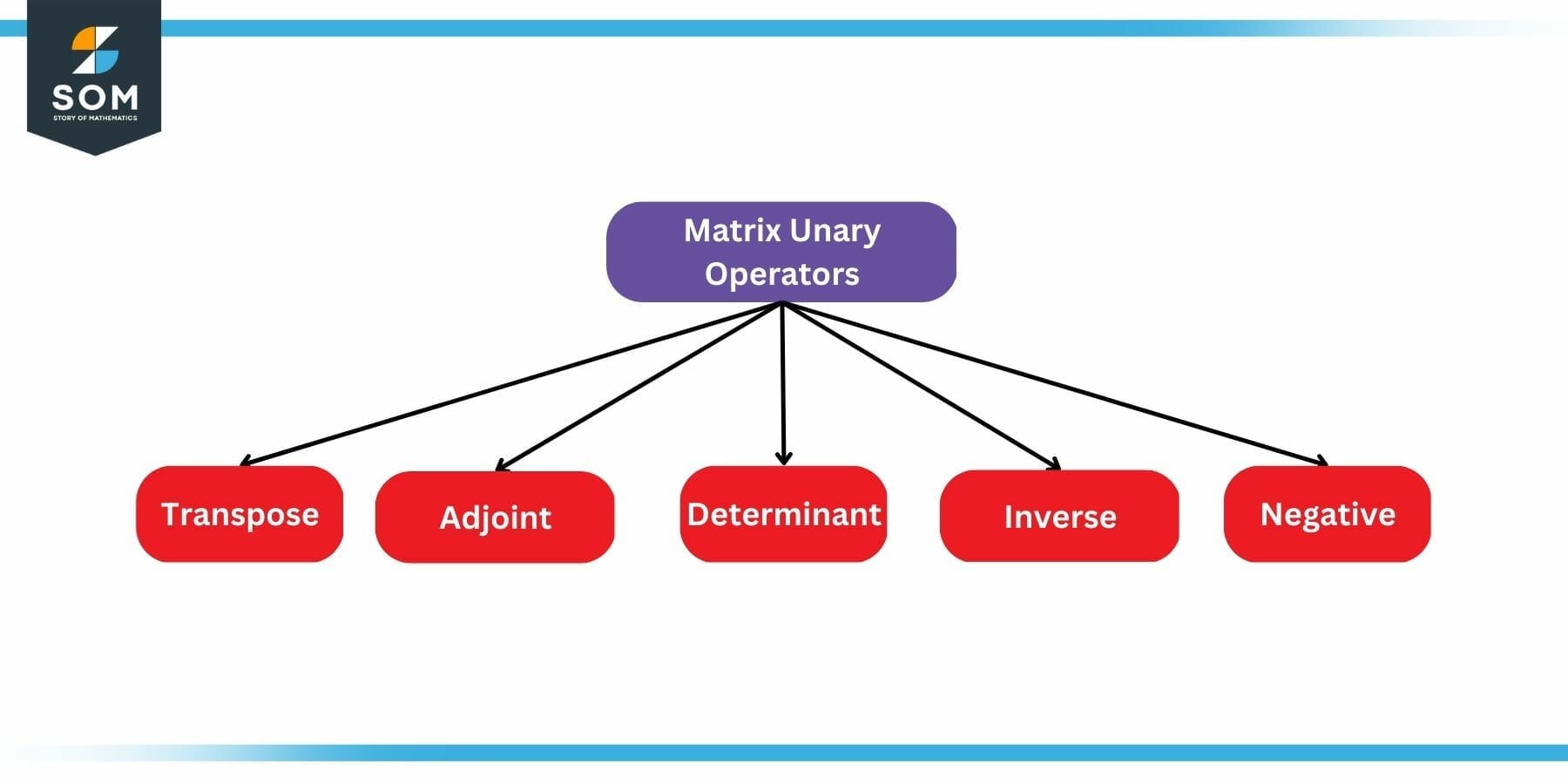
Figure 3: Matrix Unary Operations

Matrix Transpose: Transpose of a matrix is obtained by interchanging its rows and columns.

Adjoint of a Matrix: Adjoint of a 2×2 matrix is defined as the matrix obtained by interchanging the values on the main diagonal while multiplying off-diagonal values with -1.

Determinant of a Matrix: The determinant of a 2×2 matrix is a unary operation that is defined as the multiple of diagonal entries minus the multiple of non-diagonal entries.

Inverse of a Matrix: Inverse of a 2×2 matrix is a unary operation defined as the ratio of the adjoint of the matrix to the determinant of the same matrix.

3. Programming Unary Operations

Programming languages help us build usable software on a higher level. However, they are fundamentally just some mathematical operations. Some unary operations are commonly used in this domain, which are summarized in the figure below:

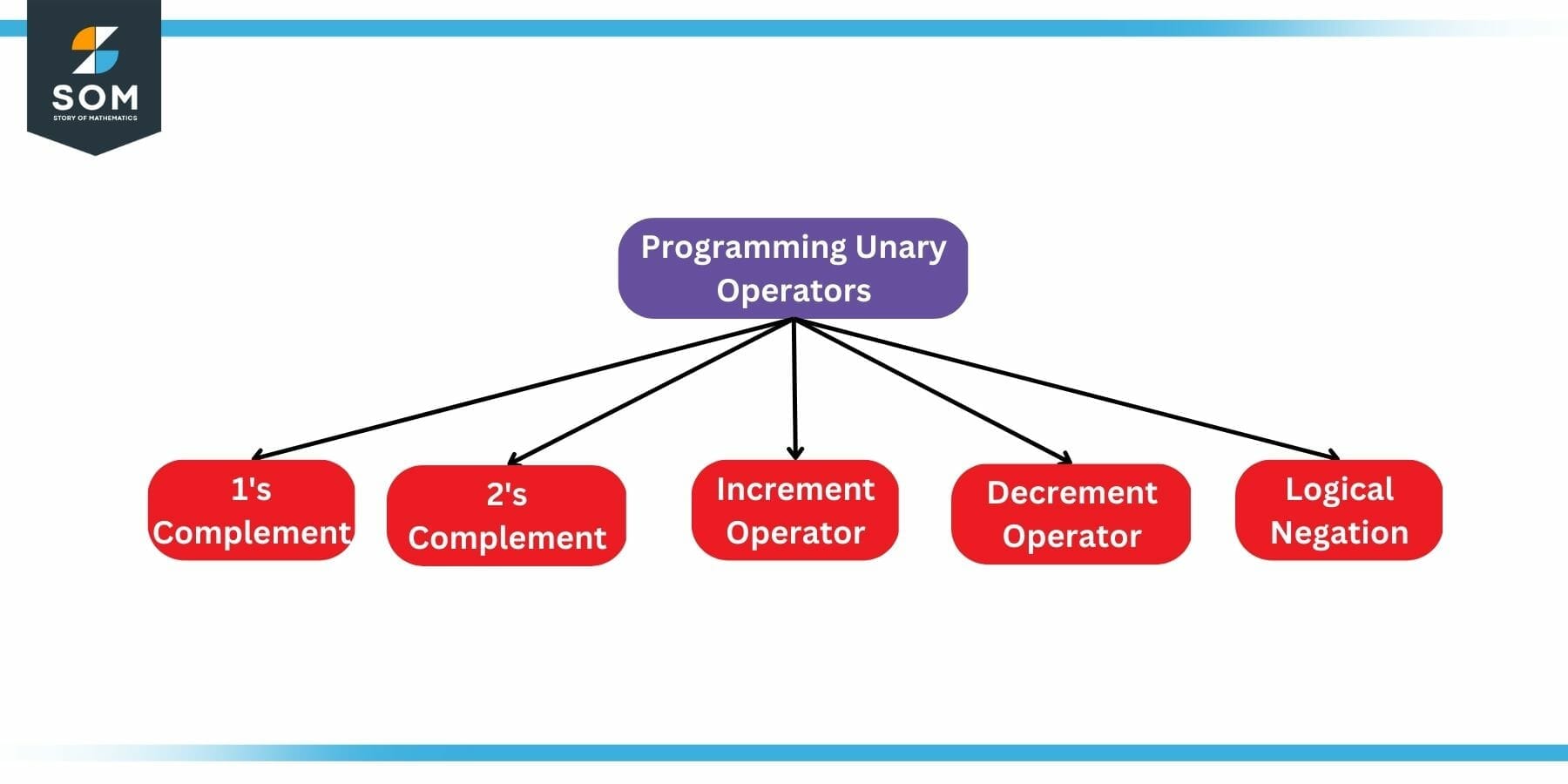
Figure 4: Programming Unary Operations

(a) 1s Complement: 1’s complement is used for subtraction purposes in the domain of the binary number system. It is a unary operation. To find the one’s complement of a given binary number, we simply invert all values. For example, to find the 1’s complement of a binary number (1010101), we invert it, which returns (0101010), which is the 1’s complement of the original number.

(b) 2s Complement: 2’s complement is also used for subtraction purposes in the domain of the binary number system. It is a unary operation. To find the one’s complement of a given binary number, we simply invert all values and add 1 to the 1’s complement. For example, to find the 2’s complement of a binary number (1010101), we invert it, which returns (0101010) + 1 = (0101011), which is the 2’s complement of the original number.

(c) Increment: Increment operation is a unary operation that adds one to the input number. For example, incrementing a number 4 would return 4+1 = 5 as the output

(d) Decrement: Decrement operation is a unary operation that subtracts one from the input number. For example, decrementing a number 4 would return 4-1 = 3 as the output

Numerical Examples of Unary Operations

Example 1

Find the absolute value of -100.

Solution

Absolute value of -100 = -1(-100) = 100.

Example 2

Find the additive inverse of 21.

Solution

Additive inverse of 21 = -1(21) = -21.

Example 3

Find the multiplicative inverse of 5.

Solution

Multiplicative inverse of 21 = -1/5.

All images were created with GeoGebra.

Twice Definition < Glossary Index > Undecagon Definition