Twice|Definition & Meaning

The mathematical operation known as “twice” is the product of a number being multiplied by 2. It is utilized to determine the value that is twofold that of a specific integer. The expression “twice the number x” is what the symbol “2x” stands for. 

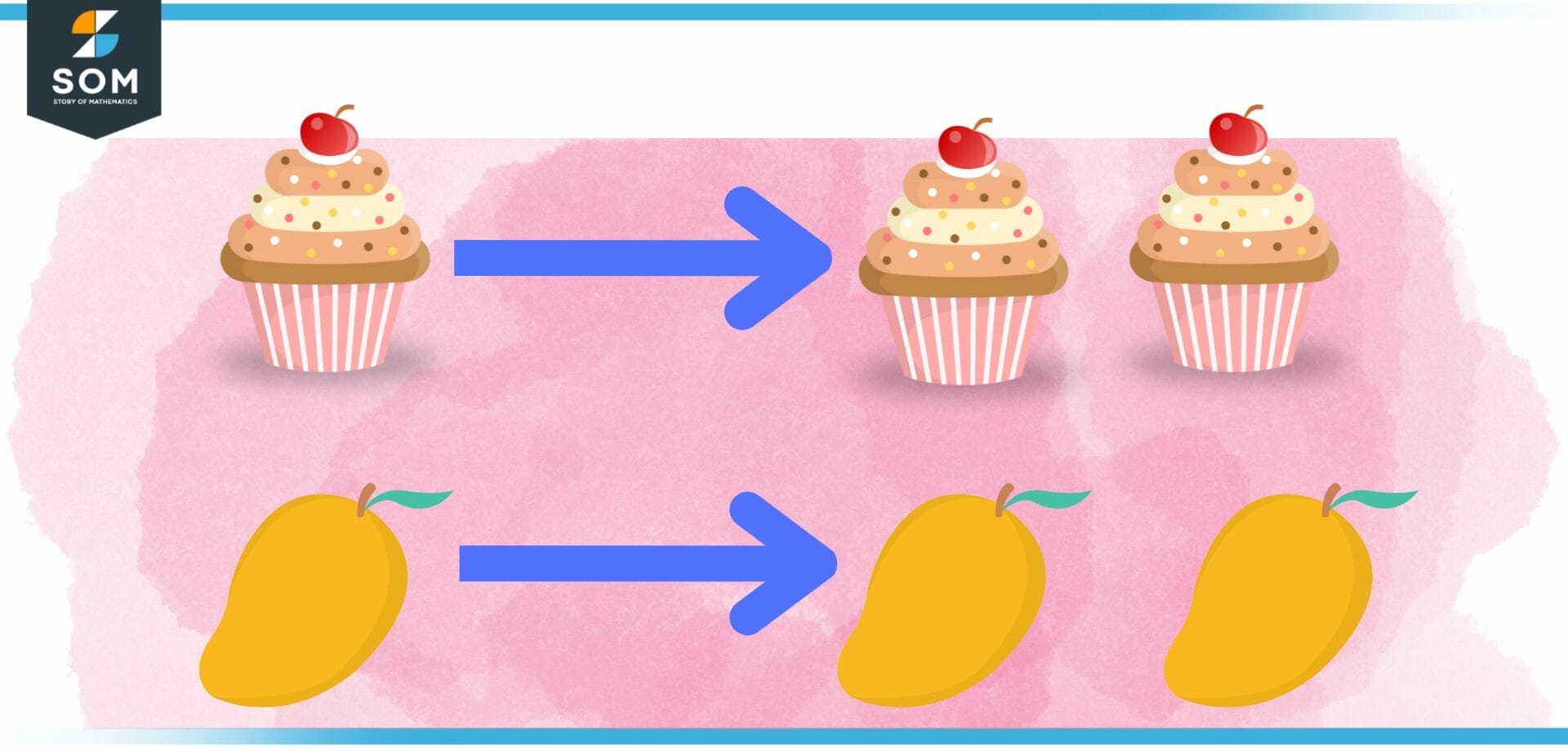
Figure 1 – Twice of cake and Mangoes

Because it is equivalent to two times the value of the number that is being given, it is sometimes referred to as double or two times the number. If you already know a number, for example, 5, and you want to find out how many times that number is, you would multiply 5 by 2, which would give you the answer 10.

Consider it in terms of the sum obtained by adding the number to itself. This is still another way to think about it. For instance, if you have a number a, the expression “twice a” can also be represented as x + x, which indicates adding the number a to itself. In this case, “twice a” refers to the product of the two numbers.

This is due to the fact that adding a number to itself after multiplying it by 2 is the same as multiplying it by 2.

Imagine that you already have four chocolate bars in your possession, and then someone gives you another four of them. You went from having four chocolate bars to have eight of them in your possession. Because four plus four equals eight, eight is the same as four times, which means you have twice as many chocolate bars as you did before.

The idea of “twice” is significant in the field of mathematics since it is applied in a wide variety of subfields, such as arithmetic, algebra, geometry, calculus, probability, and statistics, to name a few of these subfields. For example, in math, the word “twice” can be used to figure out how much anything is multiplied by two.

In algebra, it is possible to utilize it to solve equations and find variables that are unknown. Calculus requires it to be done in order to determine a function’s derivative.

1. Fundamental arithmetic: The most fundamental aspect of arithmetic is the concept of “twice,” which is a fundamental building block of arithmetic and is utilized in several calculations that are performed on a daily basis, such as determining half of a number or calculating twice as much of something.
2. Algebra: In algebra, the idea of “twice” is employed to solve equations and find variables that are unknown. When trying to solve mathematical issues involving variables, having a solid understanding of the properties of “twice” is absolutely necessary.
3. Geometry: In geometry, the term “twice” is utilized in the process of determining the diameter of a circle, which is equal to the length of the radius multiplied by two. This is but one illustration of how the idea of “twice” can be applied in different ways to different geometric problems.
4. Calculus: The idea of “twice” is used in calculus to locate the value of a function’s derivative, which may be discovered by applying the definition of the function. In order to solve calculus issues and determine the rate of change of a function, it is essential to have a solid understanding of the properties of the “twice.”
5. Probability and statistics: In the fields of probability and statistics, the expected value of a random variable can be determined by taking the average of all of the potential values. This average is frequently calculated as the sum of the probabilities multiplied by two.

As a whole, the idea of “twice” is a fundamental building element of mathematics, and it is employed in a variety of contexts throughout the field of study. To achieve success in mathematical studies and in the solving of problems that occur in the real world, it is vital to have a solid understanding of its properties and applications.

Twice Differentiable

• Twice differentiable refers to the function’s twofold derivative.
• The existence of a function’s second derivative is evidenced by the fact that the function can be differentiated twice.
• The function’s maximum and minimum values can be determined once it has been shown to be twice differentiable.
• The function reaches its maximum value when y = b if f”(y) is less than zero at that point.
• The function has reached its minimum value when the variable y = b if and only if f”(y) is greater than zero at that point.

Properties of Twice

It is essential to have a solid understanding of numerous fundamental aspects of the mathematical concept of “twice,” including the following:

1. Commutativity: Commutativity states that the result of multiplying a number by 2 is unaffected by the sequence in which the multiplication is performed. For example, 2 x a = a x 2.
2. Associativity: When multiplying by 2, it does not matter how you put the numbers together; the result will always be the same. For example, (2 x a) x b = 2 x (a x b).
3. Distributivity: The concept of distributivity states that multiplying a number by 2 and then adding it to another number has the same result as first multiplying each number by 2 and then adding the products of those two multiplications. For instance, 2 x (a + b) = 2a+ 2b.
4. Identity: The sum obtained by multiplying two numbers together is equal to zero. Hence the number 0 serves as the identity for this operation. This indicates that the answer is 0 when 2 is multiplied by 0.
5. Inverse: The inverse of multiplying a number by 2 is dividing it by 2. This indicates that if you divide a number by 2, you will end up with the same number that you started with. For instance, a = 2 x b, then b = a / 2.

Because of these features, we are able to simplify and find solutions to mathematical problems that include the “twice.” Acquiring a fundamental familiarity with the features that “twice” possesses is necessary for success in a wide variety of mathematical endeavors, including but not limited to arithmetic, algebra, geometry, and others.

Near Twice

A number that is very close to twice is referred to as a near twice. For instance, the sum 8 + 7 is considered to be close to the Twice number 7 + 7, which is the reason why it is near twice. A number that is close to twice might be expressed as twice plus one, twice plus two, or twice minus one.

For example, what is 4 plus 3? 4 equals 3 minus 1.

Therefore, 4 plus 3 can be represented as in the figure:

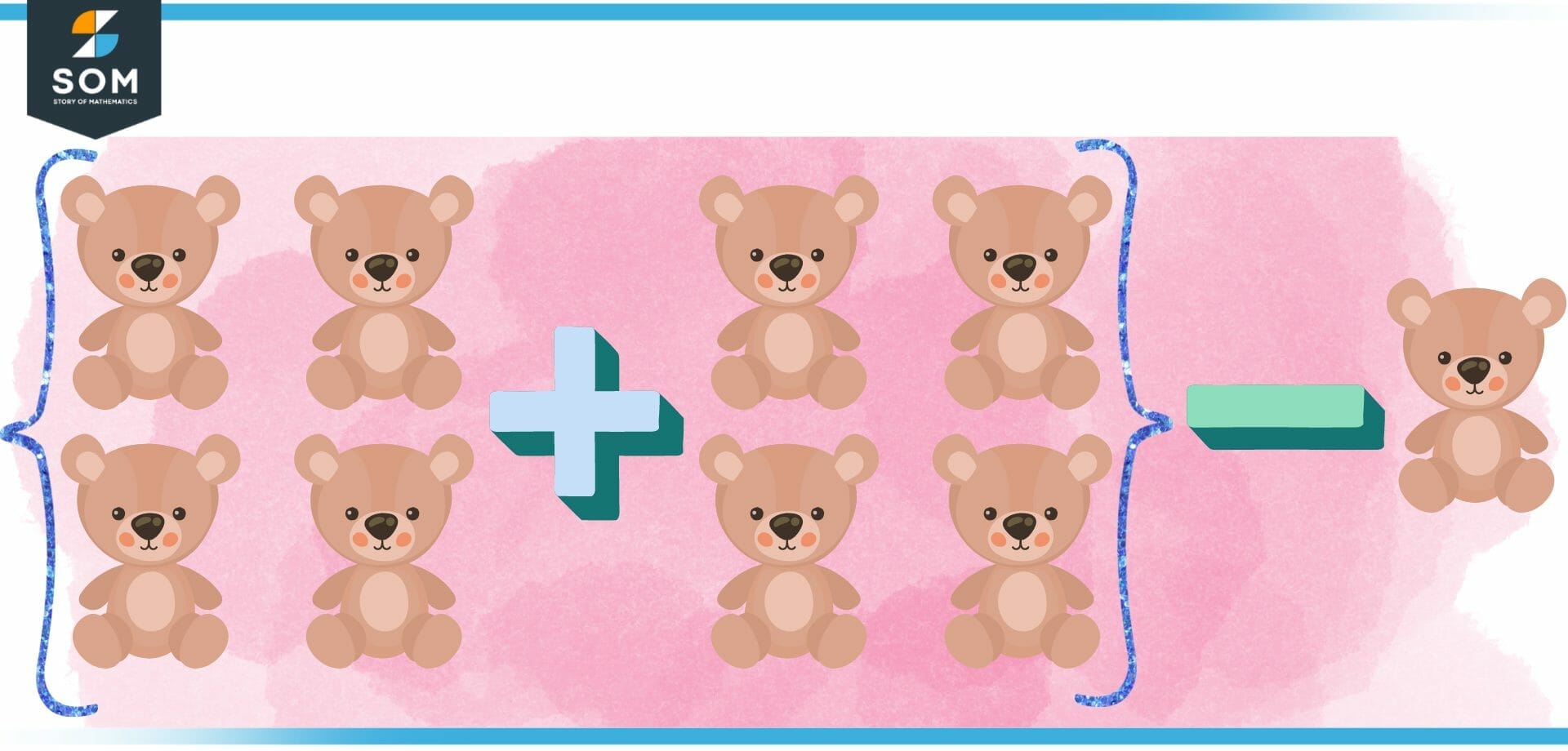
Figure 2 – Graphical depiction of near twice

We are aware that the answer to “twice of 4” is “8.”

Therefore, the required sum is 7, which may be calculated as 8 minus one or 7 total. Therefore, 4 plus 3 equals 7.

It is also possible to refer to “Twice plus 1” and “Twice minus 1” as “near Twice.”

You might also apply it to the numbers that are not directly adjacent to one another in the list.

Twice  in Subtraction

Using Twice, we can quickly and easily subtract two numbers.

For example, evaluate 12 − 6.

It is common knowledge that 6+6=12. Therefore, 12 is twice as much as 6.

12 – 6 = 6

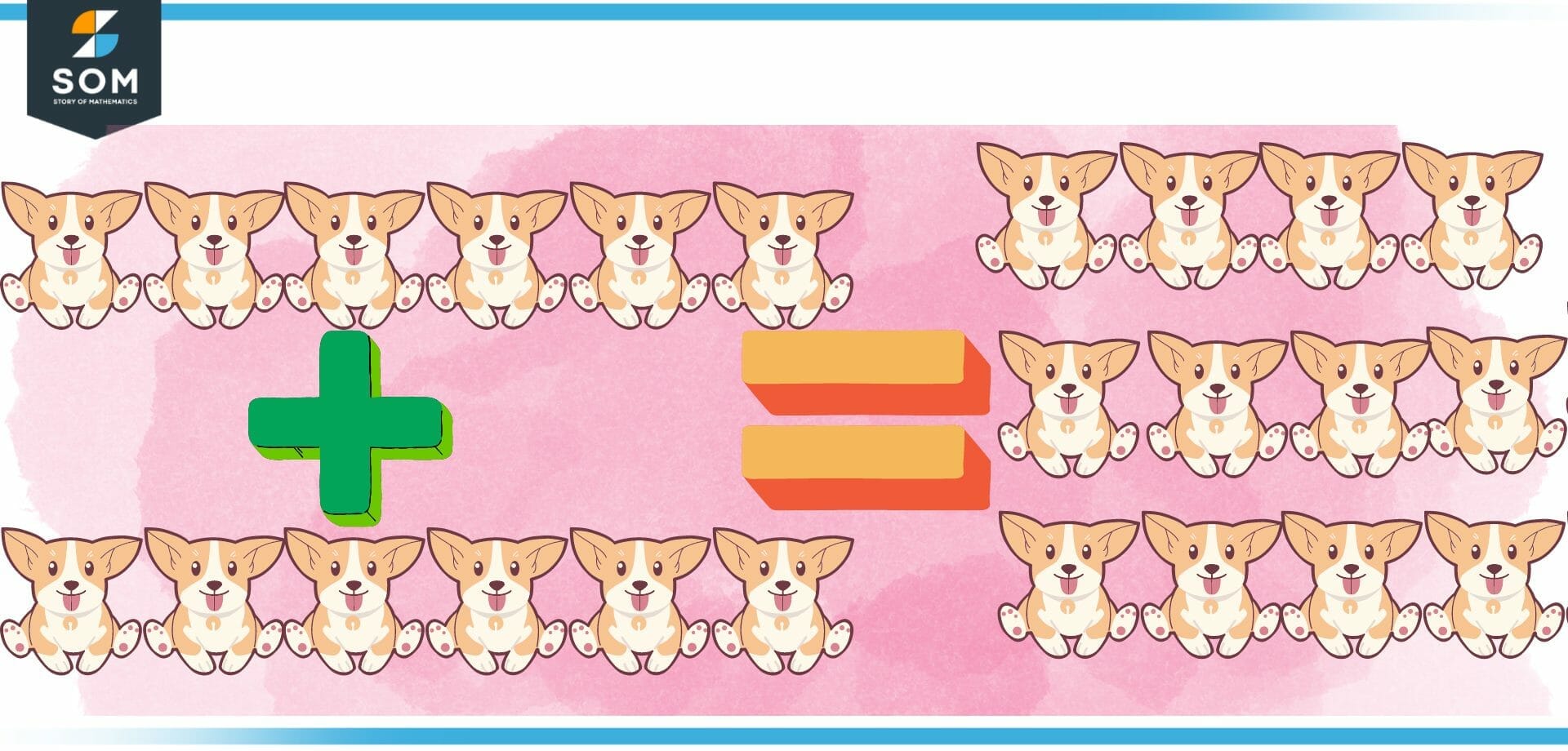
Figure 3 – Graphical representation of how adding six twice results in twelve.

One example might be: If we subtract 6 from 12, we get the amount that is still available is 6.

Advanced Concepts of  Twice

In addition to the fundamental characteristics of the word “twice,” it is essential to have a firm grasp on the following advanced mathematical principles that are connected to the process of multiplying numbers by two:

Higher-Order Derivatives: The idea of “twice” can be expanded to include higher-order derivatives, such as the third derivative and beyond. In mathematics, a function is said to be n times differentiable if it can be differentiated in n different ways.

1. The Taylor Collection: A representation of a function in the form of an infinite series is known as a Taylor series. This type of representation of a function is useful for approximating the value of a function close to a particular point. In a Taylor series, the coefficients are determined by the derivatives of a function, including the function’s second derivatives.
2. Matrix Operations: The idea of “twice” can also be extended to matrices, where it is used to represent scalar multiplication. This can be done by extending the concept of “twice” to matrices. This makes it possible to conduct an analysis of linear transformations in two-dimensional or higher-dimensional spaces, including rotations and scalings, for example.
3. Differential Equations: Differential equations are mathematical equations that describe the behavior of a function over time. Differential equations are a type of partial differential equation. When modeling physical processes with different forms of differential equations, such as the wave equation and the heat equation, the second derivative of a function is one of the derivatives that is utilized.
4. Optimization: Optimization refers to the process of determining either the highest possible value or the lowest possible value of a function. Because of the smoothness of their behavior, functions that are twice differentiable are frequently utilized in optimization issues. This is because the study of maximum and minimum values is made possible by the behavior of the function.

These advanced concepts provide for a greater knowledge of a variety of mathematical phenomena and their applications, and they highlight the diversity and importance of the concept of “twice” in mathematics.

Conclusion

In conclusion, the idea of “twice” functions as an essential mathematical process that may be applied in a wide variety of contexts. Understanding the fundamental properties of “twice,” such as commutativity, associativity, distributivity, identity, and inverse, is essential in many areas of mathematics, including arithmetic, algebra, and geometry.

In addition, more advanced ideas like higher-order derivatives, Taylor series, matrix operations, differential equations, and optimization all rely on the idea of “twice” and provide a deeper understanding of a variety of mathematical phenomena and their applications. These ideas can be found in advanced concepts.

In mathematics, the importance of the idea of “twice” cannot be exaggerated, and it is essential to the study and application of mathematics in a wide variety of fields and contexts.

Examples of Twice

Example 1

Determine 22 +27, keeping in mind the idea of “twice.”?

Solution

27 can be written as 22 + 5, so:

22 + 27 = 22 +22 + 5

= (22 + 22) + 5

= 44 + 5

= 49

Example 2

Joe possesses twice as many candies as Jack, who in turn possesses twice as many candies as Lily, and Lily possesses twice as many candies as Harry. What is the total number of sweets that Joe possesses if Harry has two candies?

Solution

It looks like Harry has 2 candies. Therefore, Lily has 4

Lily has a total of four candies. So, Jack has a total of 8

Jack has a total of eight candies. So, Joe is 16.

As a result, Joe has a total of 16 candies.

All images/mathematical drawings were created with GeoGebra.

Trend Line Definition < Glossary Index > Unary Operation Definition