Unit of Measurement|Definition & Meaning

Any quantity that can be measured is called a physical quantity. To measure a physical quantity, two things are needed. The first one is the unit of measurement that sets a reference amount of that physical quantity. The second one is the numerical magnitude that defines how many multiples of a physical quantity are being measured with reference to the unit of measurement.

Explanation of Unit of Measurement

The following figure describes this concept with the help of an example of the measurement of a flour bag:

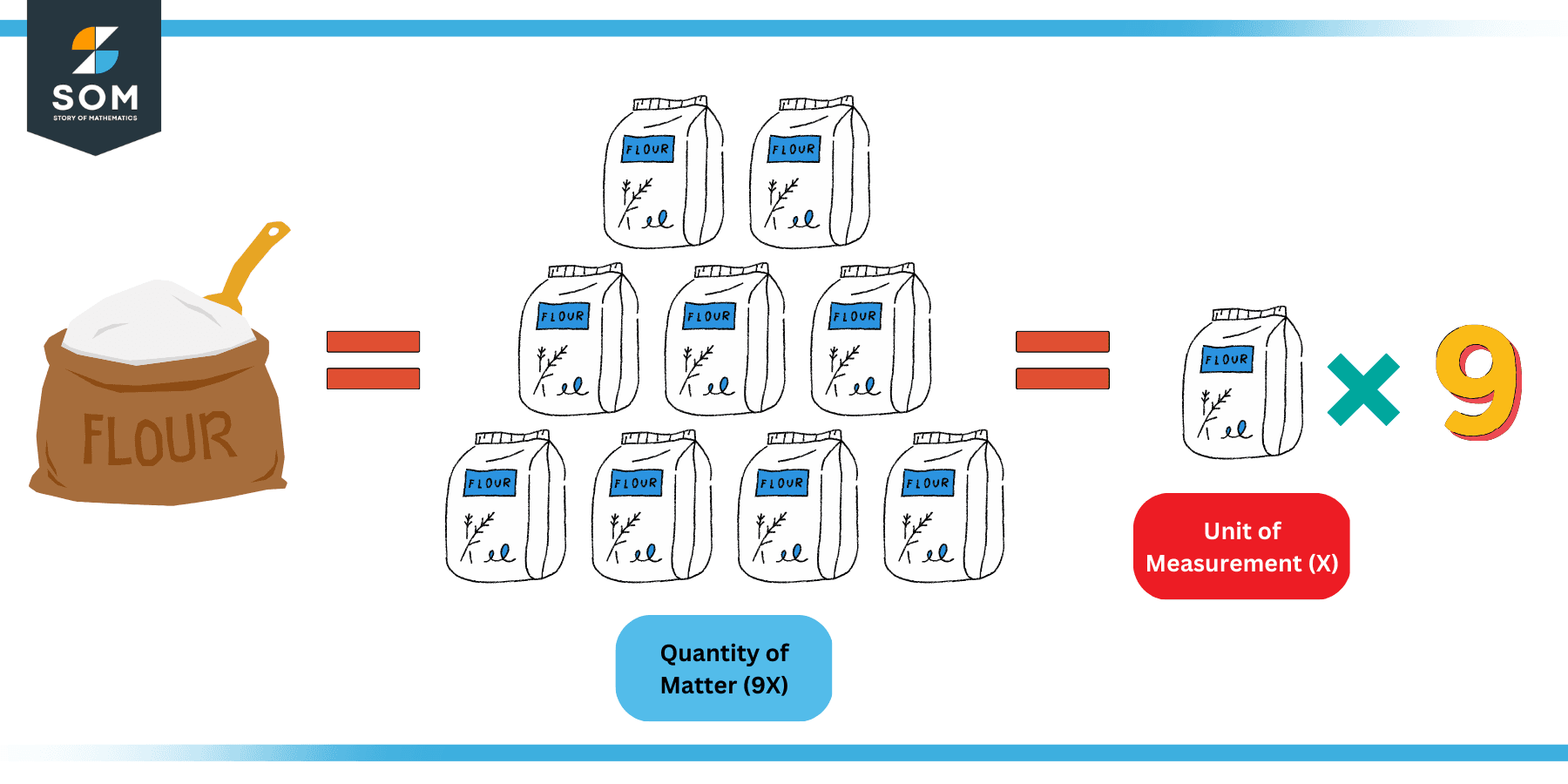
Figure 1: Flour Example of Unit of Measurement

Suppose that you wanted to measure a bigger bag of flour that you have in your store. Now you also have a 1kg bag of flour available with you in the same store. For the sake of simplicity, let us assume that the 1 kg bag is your reference and you choose it as your unit of measurement.

Now to measure the amount of flour available with you, you simply compare the available amount with the standard that you have set (that is 1kg bag). As the figure shows, you find out that you have an equivalent to nine 1kg bags of flour bags.

In this example, the smaller 1kg bag served as your unit of measurement while the number 9 represented the magnitude of the measurement.

The above unit that you defined can’t be used universally since the 1kg bag you used may lose its weight over time, and there is a chance that everybody may not be comfortable using your unit of measurement for theirs. This, indeed, has been the main problem with such units.

Over the rich history of mankind, many units have been devised for many physical quantities in different parts of the world. Naturally, these different units of measurement have caused many problems in terms of global trade and interoperability.

Therefore, the international community felt the need to develop a standardized set of units of measurement to be used worldwide.

The worldwide acceptable units of the measurement system, known as the international system of units, define some basic units of some basic quantities. In fact, there are only seven such units. These units are called base units, and the physical quantities that these units measure are called base quantities.

The units of all other physical quantities can be derived from these seven base units. These are called derived units, and the physical quantities that they measure are consequently called derived physical quantities in this context. The following figure shows these seven base units.

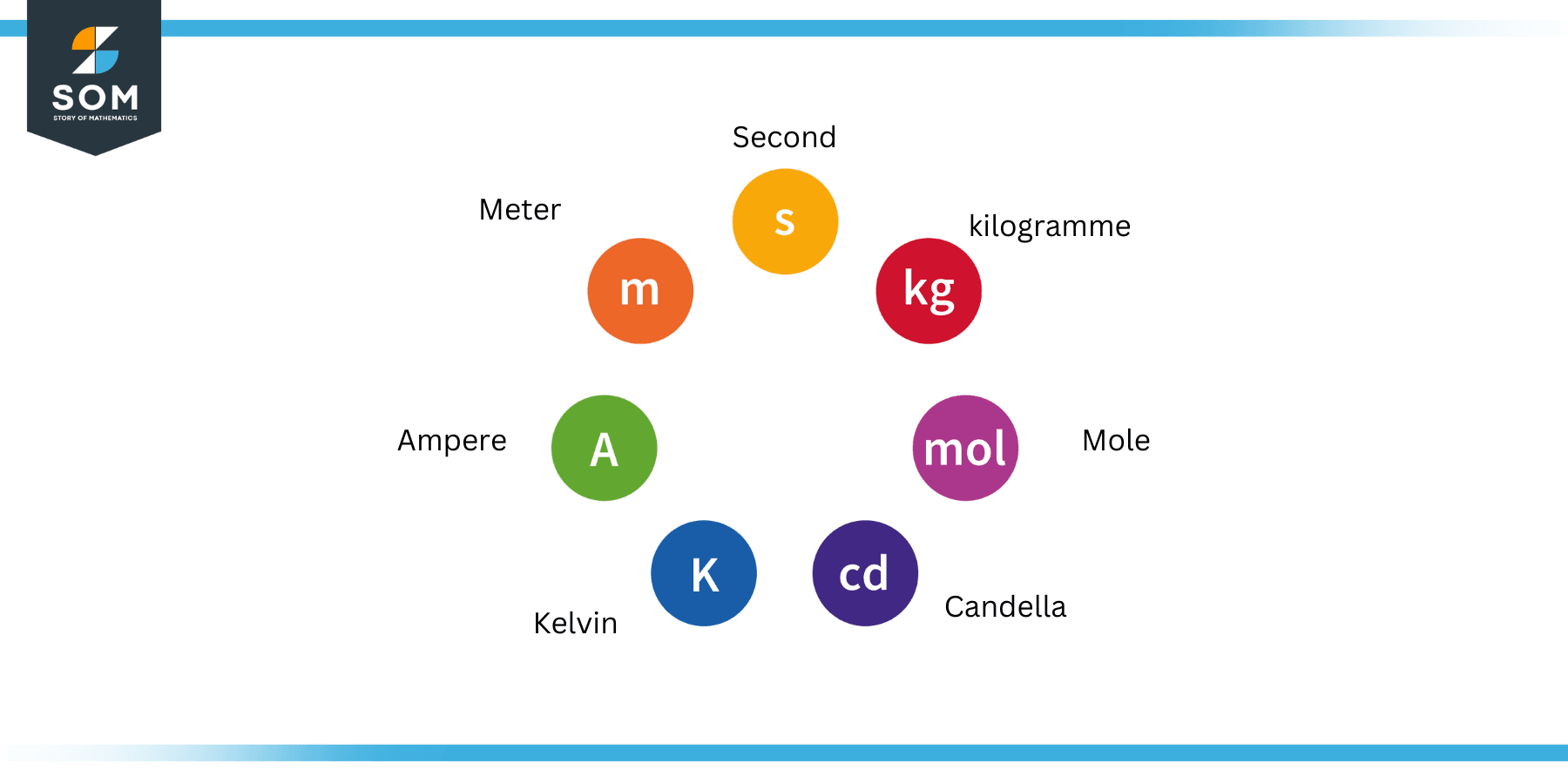
Figure 2: The Seven Base Units of Measurement

These units include second, meter, kilogram, candela, ampere, kelvin, and mole. They are used to measure time, distance, mass, the intensity of light, electric current, temperature, and quantity of matter.

Each of these base units is actually standardized. One second, for example, is defined as the time equivalent of 9,192,631,770 cycles or wavelengths emitted by the cesium-133 atom when one of its electrons jumps from one energy level to another level. This is why we often hear that the cesium clock is the standard clock.

Similarly, one meter is defined as the distance traveled by a photon of light in the vacuum during a time equal to 299,792,458th part of the standard second. Again, we are being very specific here.

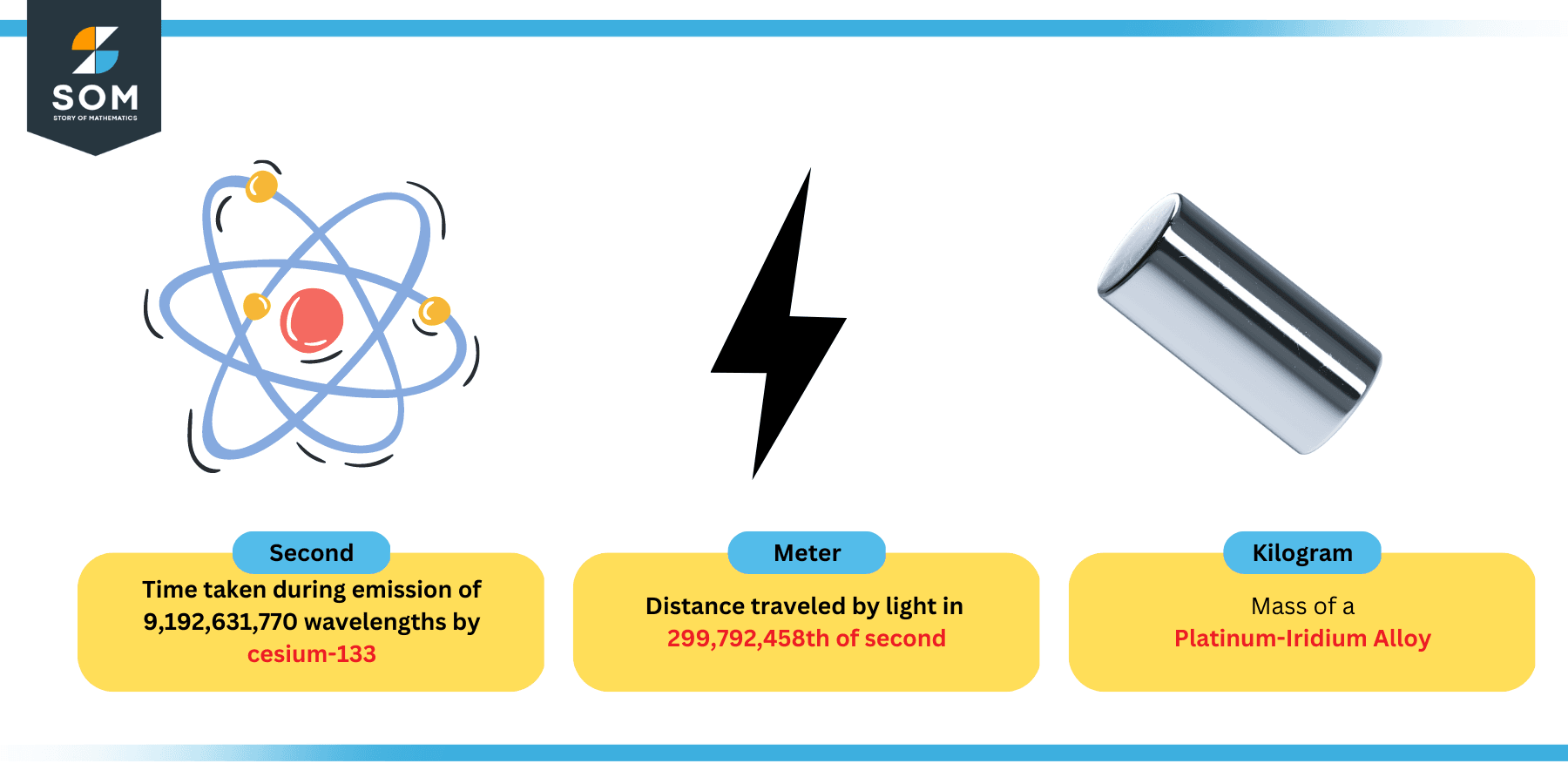
Figure 3: Definitions of second, meter, and kilogram

One kilogram is defined as the mass of a special piece of alloy made of platinum-iridium kept securely at the international bureau of weights and measures.

Prefixes of Units of Measurement

Sometimes or for some measurements, the standard units defined by the international community are either too large or too small for the purpose of measurement. For example, what if you wanted to measure the mass of one of your hair.

Now kilogram is not a suitable unit since its mass is very small compared to the mass defined by a kilogram. Similarly, what if you wanted to measure your age? We all know that seconds is a very small unit for this purpose.

To resolve this issue, prefixes were introduced. These are the multiples added to the units to make them larger or smaller as per the requirement of the application. Let us consider the example of prefixes of meter for simplicity and understanding.

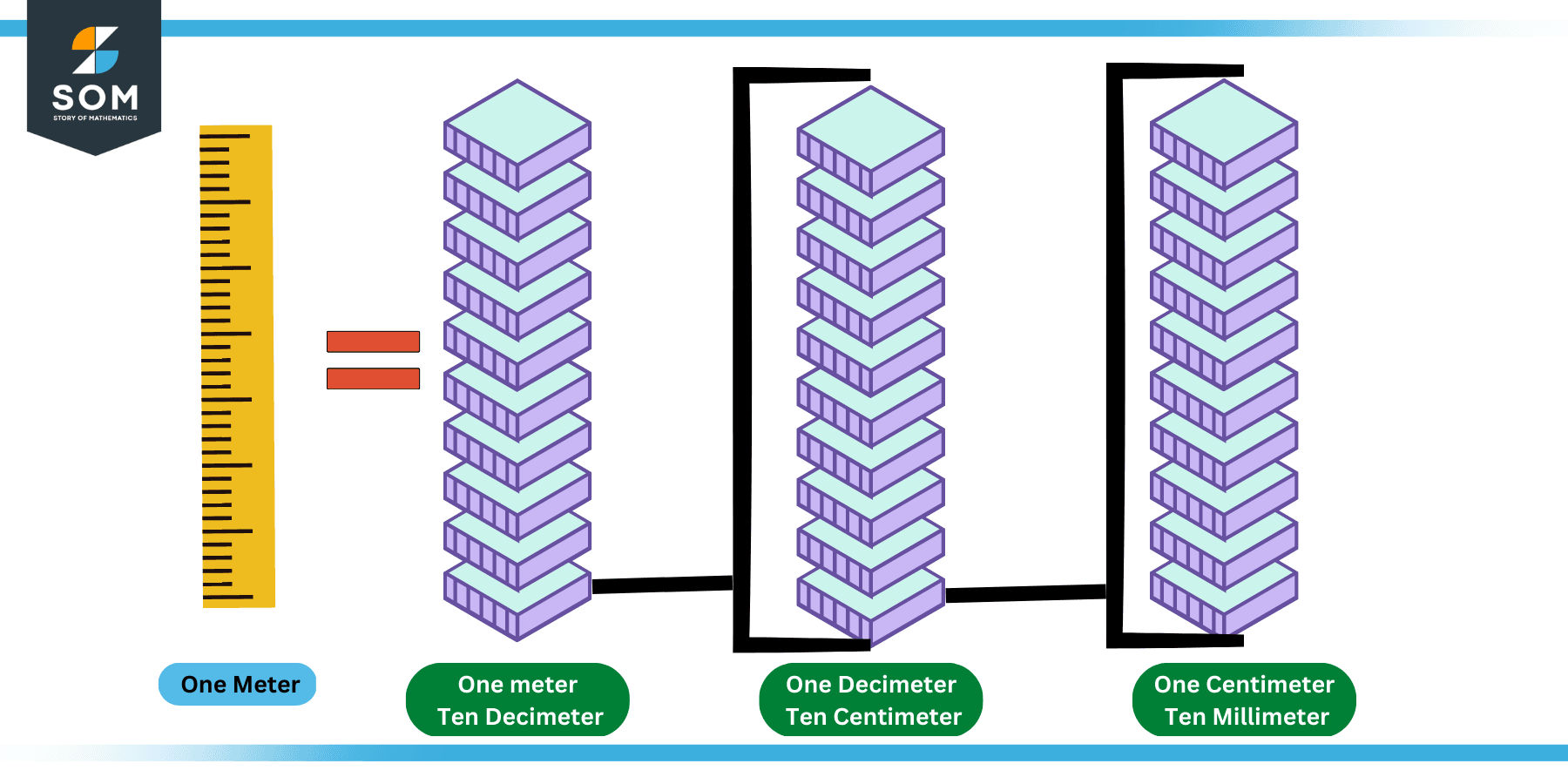
Figure 4: Prefixes of Meter

We have all heard about millimeters, centimeters, and decimeters. These are the prefixes that reduce the size of the meter by 1/1000, 1/100, and 1/10 of the original scale for the purpose of measurement of smaller distances. It can also be noticed that:

1 meter = 10 decimeter = 100 centimeter = 1000 millimeter

Similarly, we have also often used or heard of kilometers. One kilometer is equal to 1000 meters, and it is used to measure larger distances.

Derived Units of Measurement

As we mentioned earlier, many units of different physical quantities can be derived based on the standard base units (seven) given above. Now let us see how we do this. Consider the example of speed. Now we know that speed is defined as the distance covered in unit time. Mathematically:

\[ \text{Speed} = \dfrac{ \text{Distance} }{ \text{Time} } \]

Now to find its derived units, we simply plug in the units of distance and time in the above formula like so:

\[ \text{Unit of Speed} = \dfrac{ 1 \text{ meter} }{ 1 \text{ second} } \]

This implies that:

Unit of Speed = 1 meter / second

Hence, the unit of speed is 1 meter per second, written as 1 m/s. You can see how simple it is to derive or define new units based on our existing system.

Numerical Problems

Part (a): Convert 100 millimeters into centimeters.

Part (b): Convert 1 kilometer into decimeters.

Part (c): Derive the unit of a physical quantity X = (mass)(length).

Solution to Part (a)

Since:

1 meter = 1000 millimeter

1 meter = 100 centimeter

1000 millimeter = 100 centimeter

Dividing both sides by 10:

100 millimeter = 10 centimeter

Which is the required solution.

Solution to Part (b)

Since:

1 kilometer = 1000 meter

1 meter = 10 decimeter

So:

1 kilometer = 1000 x 10 decimeter = 10000 decimeter

Which is the required solution.

Solution to Part (c)

From the definition of physical quantity:

X = (mass)(length)

Its unit can be derived by plugging in the standard units of mass and length:

Unit of X = (unit of mass)(unit of length)

Unit of X = (1 kilogram)(1 meter)

Unit of X = 1 kilogram meter

Which can be symbolized by 1 kgm.

All images/mathematical drawings were created with GeoGebra.