JUMP TO TOPIC
Upper Bound|Definition & Meaning
Definition
For a given set of data, the upper bound is such a large value (not necessarily within the set) that all other values are either less than or equal to it. For example, in the set {50, 30, 25, 100, 3}, all numbers from 100 and onward are valid upper bounds. The upper bound tells us that our result cannot be bigger than it, which is useful when we are dealing with uncertain behavior.
What Is an Upper Bound?
An upper bound in mathematics is simply the highest value that a set of numbers or variables can attain. It’s like a ceiling on the maximum value that can be reached, and every value in the set has to be less than or equal to this upper bound.
The concept of an upper bound works hands in hand with that of a lower bound, which is the minimum value in the set. The two bounds together create the range of values that the set can take.
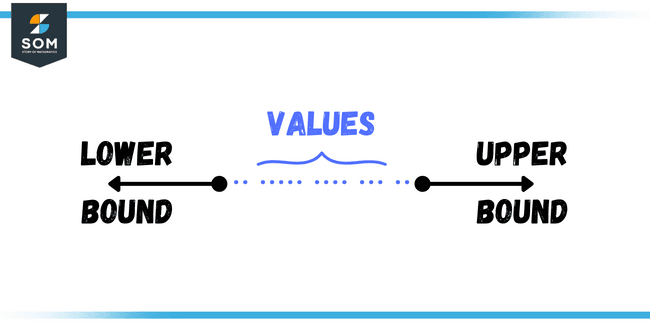
Figure 1 – Upper bound and lower bound of a set of values
Upper bounds play a significant role in mathematics, as they can be applied in various fields such as real analysis, number theory, and combinatorics. For instance, in real analysis, upper bounds are used to find the supremum, which is the smallest real number that is equal to or greater than all elements in a set of real numbers.
These bounds also play a key part in determining the limit of a function, which is the value that the function approaches as the input values come closer and closer to a specific value.
Upper Bound Vs. Lower Bound
Upper and lower bounds are critical ideas in mathematics that administer to represent the scope of values a particular set of numbers or variables can endure. These bounds play a part in a variety of mathematical fields, such as real analysis, number theory, and combinatorics.
An upper bound represents the highest value a set of numbers or variables can attain. It acts as an upper limit and is greater than or equal to all other values in the set. When dealing with real numbers, the smallest real number that is greater than or equal to all elements of the set is known as the supremum, or least upper bound.
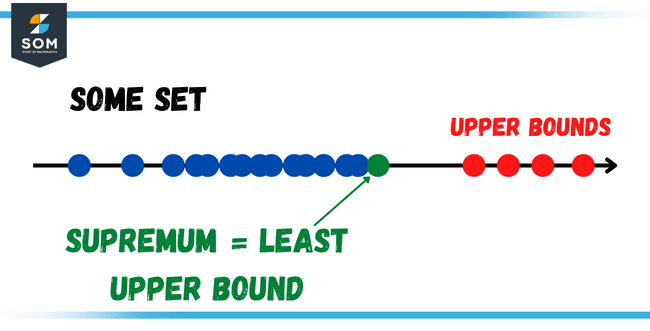
Figure 2 – A visual representation of supremum of a set
On the other hand, the lower bound represents the lowest possible value that a set of numbers or variables can attain. It acts as a lower limit and is less than or equal to all other values in the set. Together, the upper and lower bounds provide a comprehensive view of the possible range of values for a set of numbers or variables.
How to Find Upper Bound?
Finding upper bounds is an important skill in mathematics and has a wide range of applications, including real analysis, number theory, and combinatorics. To find an upper bound, we need to determine the highest possible value that a set of numbers or variables can attain. This value acts as the upper limit to the possible values in the set.
There are several methods that can be used to find upper bounds. One of the simplest ways is to simply look at the set of numbers or variables and determine the largest value. This value is then considered to be the upper bound. Another method involves using mathematical concepts such as supremum and limit of a function.
The supremum of a set of real numbers is defined as the smallest real number that is greater than or equal to all elements of the set. In real analysis, the concept of an upper bound is used to define the supremum or least upper bound. Additionally, the limit of a function can be used to determine the value that the function approaches as the input values get arbitrarily close to some value.
One thing to note here is that upper bounds can occasionally be tricky to determine, particularly for extensive and complicated sets of digits or variables. In such circumstances, it may be essential to use avant-garde mathematical notions and strategies to uncover the upper bound accurately.
Upper Bounds in Number Theory
In number theory, the notion of an upper bound plays a crucial role in exploring the characteristics and connections between numbers. It represents the highest value that a set of numbers can possibly reach, serving as an upper limit.
Upper bounds are especially useful in studying Diophantine equations, which are mathematical expressions composed of only integers and seek integer solutions.
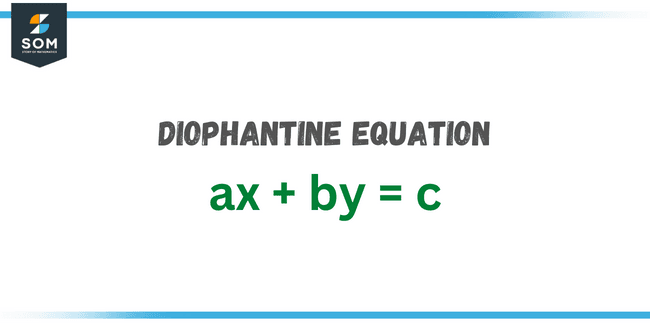
Figure 3 – A Diophantine equation
By using upper bounds, researchers can determine the presence and quantity of solutions for a Diophantine equation. For instance, by finding the maximum value of one of the variables, the range of possible values for the other variable can be deduced.
Another area where upper bounds are used extensively is in Diophantine approximations. This is the process of locating rational numbers that closely approximate a given real number. The utilization of upper bounds helps in determining the precision of a Diophantine approximation by setting a maximum limit for the error that can occur.
Use of Upper Bounds in Calculations
When it comes to making calculations, upper bounds can be a useful tool for determining the highest possible value that a set of numbers or variables can attain. By setting an upper limit, you can get a sense of the range of values that a set can take and make more informed decisions based on that information.
To use upper bounds in calculations, it’s important to first identify the set of numbers or variables that you’re working with. Then, you’ll need to find the highest value in the set and compare it to all other values to ensure that it is indeed the upper bound.
Once you have determined the upper bound, you can use it in a variety of ways, such as:
- To determine the range of values that a set can take: By using the upper bound in conjunction with a lower bound, you can get a sense of the full range of values that a set can take.
- To establish limits in a calculation: If you’re working with a calculation that involves a set of numbers, you can use the upper bound to establish limits on the calculation and make sure that the final result is within the desired range.
- To compare values: By using upper bounds, you can compare the highest possible value of one set to the highest possible value of another set and make determinations about which set is larger, smaller, or equal.
Using Upper Bound in an Addition
Using them in computations involves putting a limit to the attainable values that can be acquired in a mathematical expression or equation. This significantly benefits us in facilitating and constructing calculations more effortlessly.
Let’s say we have an expression 2x + 5. If we know that x is a positive integer and its maximum value is 10, we can specify an upper bound for the expression as 2 * 10 + 5 = 25. This means that the highest possible value that 2x + 5 can attain is 25. By using this upper bound, we can quickly determine that 2x + 5 can never be greater than 25, which can significantly simplify our computations.
Using Upper Bound in Subtraction
Like in addition, upper bounds can also be used in subtraction to specify the maximum disparity between two numerals. To use them in a subtraction scenario, you might want to first figure out the upper bound of those numerals which are being subtracted.
Consider a scenario where you have two numbers, 5 and 10, and you want to find the maximum difference between these numbers. By looking at the numbers, we can say that the upper bound of 5 is 5; similarly, the upper bound of 10 comes out to be 10. So, this results in the upper bound of the difference between these two numbers, that is, 10 – 5 = 5. This indicates that the maximum difference that you can obtain by subtracting these two numbers is 5.
Using Upper Bound in Multiplication
Upper bounds also have an application in problems requiring multiplication. It is used to specify the maximum value that the product of two or more numbers can attain. Here is an example:
Let’s say you have two positive real numbers, a and b. To find the upper bound of their product, we can use the fact that the product of two positive real numbers is always less than or equal to the product of their upper bounds. So, if a has an upper bound of A and b has an upper bound of B, the upper bound of their product ab is A x B.
Let’s consider a simple example in which a = 2 and b = 3. The upper bound of a is 2, and the upper bound of b is 3. So, the final product, 2 x 3, is 6.
Using Upper Bound in Division
The upper bound in division is used to find an estimate of the maximum possible result of a division operation when the values used in the operation are rounded or have limited precision. Suppose you need to divide 1000 by 3 to get the average value of something, but you only know that 3 is between 2.5 and 3.5. To find the upper bound, you would use the maximum value of the divisor, which is 3.5 in this case:
Upper bound = 1000 / 3.5 = 286.67 (to 2 decimal places)
Solved Examples To Calculate Upper Bounds
Example 1
A rectangle has a base b of 4.67 m to 2 decimal places and a height h of 3.5 m to 2 significant figures. Find the upper and lower bounds of area A of the rectangle.
Solution
To find the upper and lower bounds of area A of the rectangle:
Upper bound:
b = 4.67 m (to 2 decimal places)
h = 3.5 m (to 2 significant figures)
A = b x h = 4.67 m x 3.5 m
= 16.34 m$^2$ (to 2 decimal places)
Lower bound:
b = 4.67 m (to 2 decimal places)
h = 3.5 m (rounded down to 2 significant figures)
= 3.0 m A = b x h = 4.67 m x 3.0 m
= 14.01 m$^2$ (to 2 decimal places)
So, the upper bound of area A of the rectangle is 16.34 m$^2$, and the lower bound is 14.01 m$^2$.
Example 2
A truck covers a distance of 470 miles in 7.2 hours, with both values rounded to 2 significant figures. Determine the upper and lower bounds of the average speed of the truck, expressed to 2 decimal places.
Solution
Using the basic knowledge to find the upper and lower bounds:
Upper bound:
distance = 470 miles (to 2 significant figures)
time = 7.2 hours (to 2 significant figures)
average speed = distance/time
= 470 miles / 7.2 hours
= 65 mph (to 2 decimal places)
Lower bound:
distance = 470 miles (to 2 significant figures)
time = 7.2 hours (rounded down to 2 significant figures)
= 7.0 hours average speed = distance / time
= 470 miles / 7.0 hours
= 67.1 mph (to 2 decimal places)
So, the upper bound of the average speed of the truck is 65 mph, and the lower bound is 67.1 mph.
All images are created using GeoGebra.
