JUMP TO TOPIC
Value|Definition & Meaning
Definition
A value is simply a number or the outcome of a computation. It can refer to several closely related concepts, but generally, a mathematical value can be any distinct mathematical object.
This is often a number associated with some quantity.
For instance, a bottle contains 300 milliliters of soda, where volume is the quantity, and 300 milliliters is its value.
Figure 1 below shows the value of the addition of numbers.
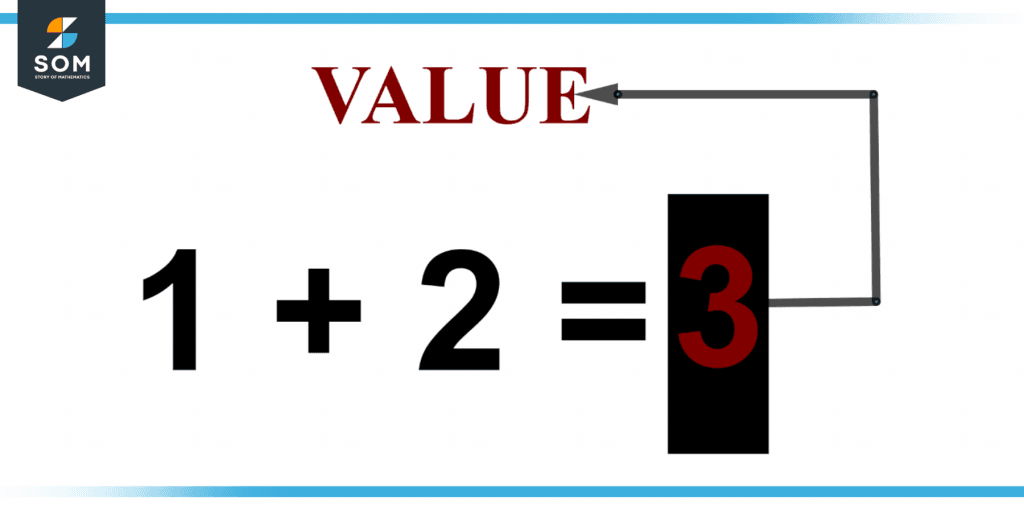
Figure 1 – Representation of value in addition.
What Is Value?
Math issues frequently call again for the “value” of a computation or phrase. Whenever a and b are equivalent to specific values, a math instructor could ask again for the value of a+b.
The value of computation or expression in mathematics is the amount that results from the applicable calculation (s). For example, if a = 1 and b = 2, value of a + b equals 3. You may be asked for the result of a computation (such as 23), a constant (such as b), a variable (such as x), an expression (such as x + y), a function (such as f(2)), and numerous other things.
The length of such a list should demonstrate how widespread the notion of value is already in math.
Understanding Value
Mean Value
The mean of a group of numbers is the average or mean value of some of those values. The mean value can be computed by combining the values and then dividing the result by the number of numbers. To find the average value given numbers 1, 2, 3, & 4, for illustration, add the numbers as 2 + 3 + 4 = 9. Because there are three numbers, divide this total by three:
\[\frac{9}{3}=3\]
As a result, the average of these figures is 3.
Function’s Value
The function’s value is the result of a method for a given value is the integer that the function returns. It is often discovered by solving the function’s formula for the supplied integer.
Given the value(s) given to its argument(s), the value of a function is the number estimated by the function for that argument value. Actual-value variables, expressions, and functions only assume real values. A complex-valued variable, equation, or function, on the other hand, simply accepts complex values.
Assume that the function f is defined by equation f (x) = 4(x) – 2. You may compute the value of f (2) using this equation by entering x = 2 into the equation and computing the result:
f(2) = 4(2) – 2
= 8 – 2
= 6
A function is something that converts inputs into outputs. Figure 2 below shows the function in which input is converted into output.
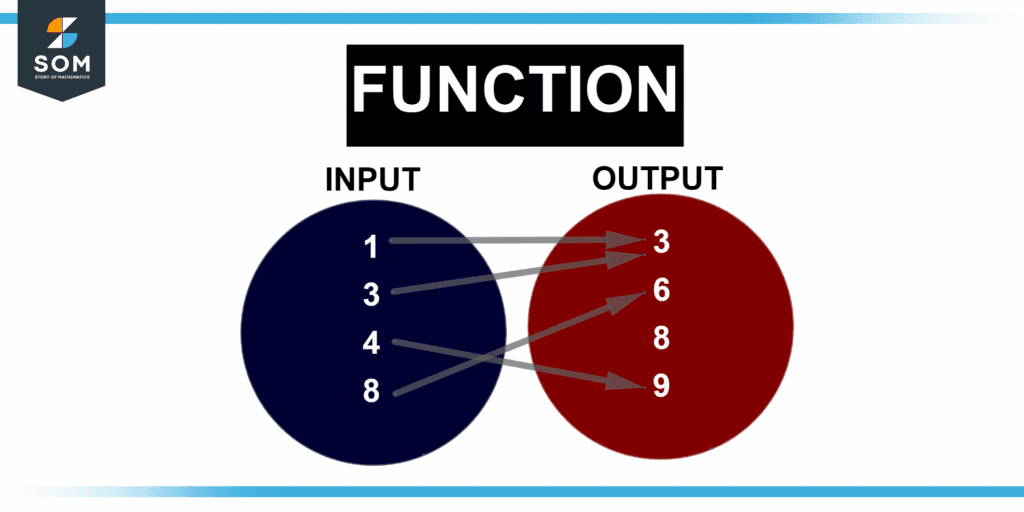
Figure 2 – Representation of value in functions.
Formula for Value
The value corresponds to the price of each digit concerning its position in the number. We compute it by combining the digit’s place and face values.
Place Value
The place value explains the worth of each digit inside a number based on its position. These slots begin with the unit’s location (one place).
From right to left, the place value of figures in a number is expressed in ones/units, tens, hundreds, thousand, ten thousand, and so on. The value of each component in a number is known as the place value. The value of each digit in quantity varies depending on its location.
A number may have two complementary digits but differing values, determined by the digit’s location in the number.
Place Value Characteristics
- Every one-digit number’s place value is equivalent to its face value.
- A place value for the 10th digit in a 2-digit number is ten times the digit.
- The number 5 is at one, the number 7 is at ten, and the number 4 is at the hundredth in the number 475.
- The basic rule is that the digit has its place value as that of the combination of the number and the place value of just one to be in that location.
Face Value
A digit’s face value in any amount is numeric. Each digit has a face value, whether 1, 2, or an integer. The number of digits included within a value is alluded to as its total price in mathematics.
Every integer has a digit, as we all know. One-digit, two-digit, three-digit, or more-digit numbers are all valid. There are various figures. Each number has both a place value and a face value.
In statistics, the quantity of a digit has been its face value.
This value is constant regardless of where it occurs in a number. Figure 3 below shows how to calculate the value.

Figure 3 – Representation of formula to find value.
Absolute Value
Absolute values are defined as the numeric values or magnitude |x| denotes the absolute value of the x variables, also known as Mod X or Modulus of X. ‘Modulus’ is a Latin word that signifies “measuring.” The absolute value represents a real number and does not include the numeric sign.
With the exception of zero, which is neither positive nor negative, an absolute value again for quantity will always be positive. An integer’s absolute value is its length from zero, independent of direction. Almost any vector quantity’s modulus is always positive and indicates its absolute value. Length, cost, capacity, and time are all provided in absolute terms.
Absolute Value Characteristics
If a and b are real numbers, the absolute values meet the following conditions:
- Non-negativity
- Positive-definiteness
- Multiplicativeness
- Subadditivity
- Symmetry
- Indiscernible identity (equal to the positive definiteness)
- Inequality in a triangle (equivalent to subadditivity)
- Division preservation (equivalent to multiplicativeness)
- Subadditivity is equivalent
Example of Value
Determine the value of 2| 3x – 4 | if x = -2.
Solution
We have the equation 2 | 3x – 4 |. We are given the value of x as -2.
Putting the value of x in the equation, we get:
= 2| 3(-2) – 4 |
By simplifying, we get:
2| 3x – 4 | = 2 | -6 – 4 |
Adding:
2 | 3x – 4 | = 2 | -10 |
2 | 3x – 4 | = 2 * 10
By multiplying, we get the answer:
2 | 3x – 4 | = 20
All images are made using GeoGebra.
