JUMP TO TOPIC
Variable|Definition & Meaning
Definition
A variable is something whose value is unknown. We usually represent variables using letters from the English alphabet (usually the last few, like x, y, etc.). For example, in x + 1 = 3, x is a variable. This equation is only true if x = 2. However, there are equations (x + y = 3) in which multiple values of the same variable are valid, so we just call them variables in general.
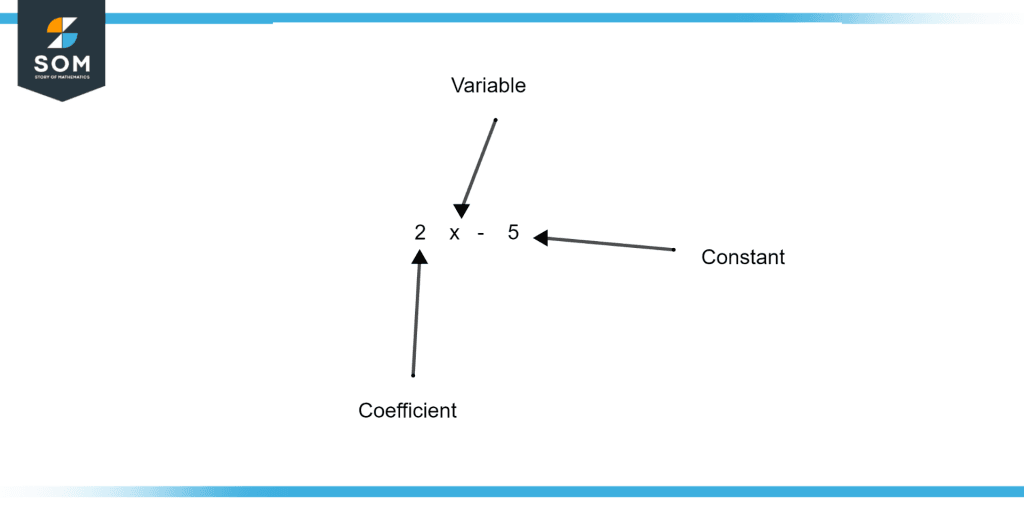
Figure 1 – Difference between Coefficient Variable and Constant
Figure 1 illustrates the difference between the coefficient, Variable and Constant.
Single letters are used to designate geometrical points and forms in prehistoric writings like Euclid’s Elements. In the Brhmasphuasiddhnta from the 7th century, Brahmagupta employed several colours to symbolize the unknowns in algebraic equations. Equations of Several Colours is the title of one chapter in this book.
The concept of expressing known and unknown numbers by letters now referred to as variables, and computing with them as if they were numbers in order to reach the answer by a simple replacement was first proposed by François Viète towards the end of the 16th century. Consonants were used for known values and vowels for unknowns according to Viète’s convention.
Typically, variables are identified by a single letter, either capitalized or lowercase, most frequently from the Latin alphabet and less frequently from the Greek. The subscript may come after the letter. Pure mathematics variable names that have been influenced by computer technology can include many letters and numbers in them.
Letters at the start of the alphabet, such as a, b, and c, are frequently used for known values and parameters, whereas the last few letters of the alphabet, such as x, y, and z, are frequently used for unknowns and variables of functions, according to René Descartes (1596-1650). Variables and constants are typically set in italic font in printed mathematics.
Equation
Two things are equal, according to an equation. It will include the equals symbol “=”. A term might be a single number, a variable, or a combination of numbers and variables multiplied. A set of terms (the terms are separated by + or signs) is referred to as an expression. An example of an equation is illustrated in figure 2.
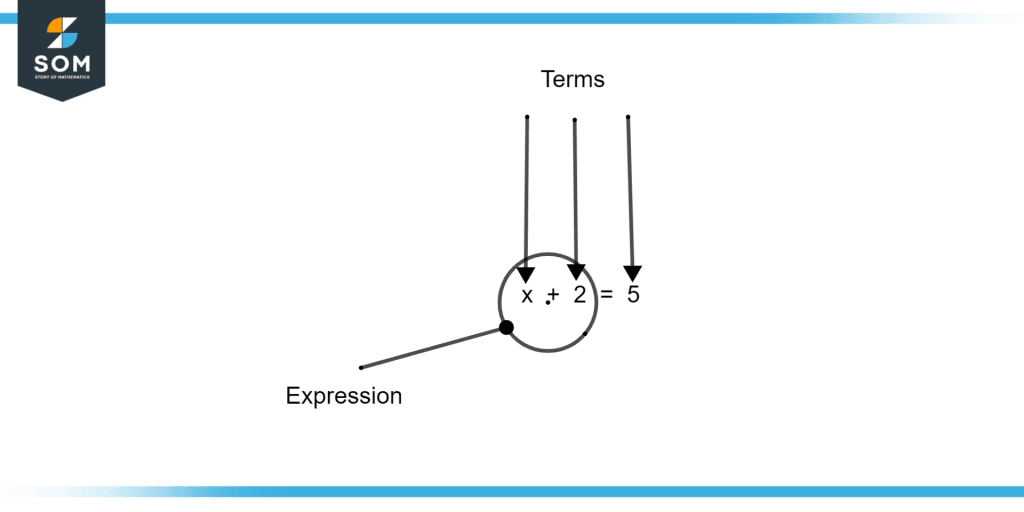
Figure 2 – Expression and terms
Exponents
The exponent (such as 2 in $x^2$) specifies how many times to use the value in the multiplication.
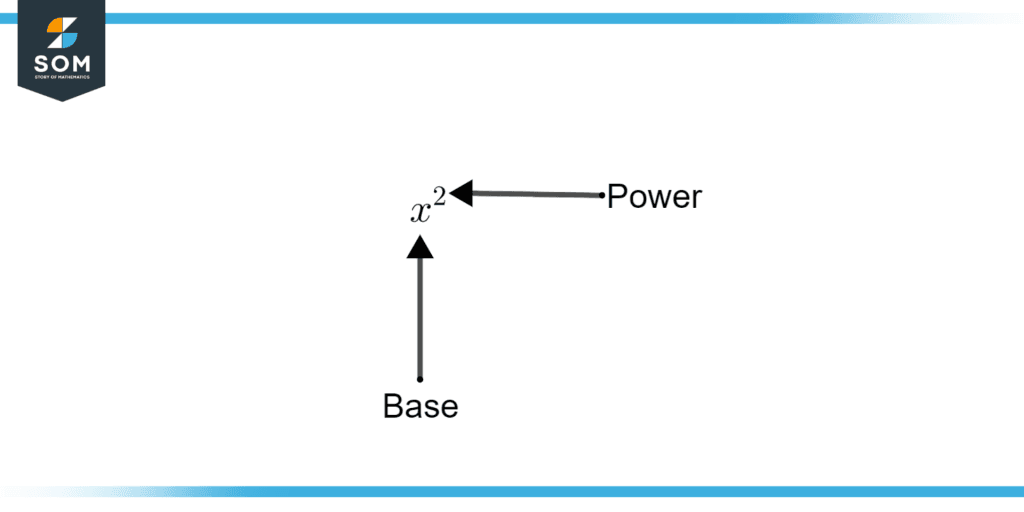
Figure 3 – Exponent
Figure 3 illustrates the exponent.
Specific Names for the Variables
A variable that has to be solved in an equation is an unknown. An indeterminate is a symbol, sometimes known as a variable, that may be found in a formal power series or a polynomial. In the ring of formal power series or the polynomial ring, an indeterminate is a constant rather than a variable.
However, due to the close connection between polynomials or power series and the functions they describe, many writers view indeterminates as a particular category of variables. A parameter is a quantity, generally a number, that is included in a problem’s input and is consistent during the whole solution process.
For instance, in mechanics, the size and mass of a solid entity are criteria for the investigation of its motion. The term “parameter” has a distinct meaning in computer science and refers to a function argument. There are bound and unbound variables. In probability theory and its applications, a random variable is a type of variable.
Types of Variable
In calculus and physics, and other scientific applications, it is fairly common to consider variables such as y, whose possible values depend on the values of another variable such as x. Mathematically speaking, the dependent variable y represents the value of a function of x.
To simplify expressions, it often makes sense to use the same notation for the dependent variable y and the function that maps x to y. For example, the state of a physical system depends on measurable quantities such as pressure, temperature, and spatial position.
All of these quantities change as the system evolves. That is, they are functions of time. In the formulas that describe the system, these variables are implicitly considered functions of time because they are represented by time-dependent variables.
The variables may be divided into two groups, including
- Dependent Variables
- Independent Variables
Dependent Variables
The term “dependent variable” refers to a variable whose evaluation of another variable in its context determines the quality of the dependent variable. That is, it is consistently claimed that the estimation of the word variable depends on the free variable of the mathematical condition.
Take the formula y = 4x + 3 as an example. In this scenario, alterations to the estimation of the variable ‘x’ cause changes in the estimation of the variable ‘y’. In this way, the variable “y” is referred to as a dependent variable. Some of the instances that include dependent variables are discussed in the point of interest below, along with their solutions.
Independent Variables
An independent variable in an algebraic equation is a variable whose values are unaffected by changes. In an algebraic equation with two variables (x and y), if any value of x is related to any other value of y, then it is said that the value of y is a function of the value of the independent variable (x), which is known as the x value, and the value of y is known as the dependent variable.
Applications of Variables
Variables are utilized not only in mathematics but also in many other disciplines for a variety of reasons, including programming, research, science, and statistics
Some Examples of Variables
Example 1
Solve the following
a) Find x in the equation 6x + 5 = 17.
b) Find y in the equation 3y + 15 = 21.
c) Find the factors of the equation x2+6x+9.
Solution
a) As this is an equation, both sides are equal, as represented by the equal sign. To find a value of x that satisfies the right-hand side (RHS) and left-hand side (LHS) of the equation, we will do some algebraic manipulations:
6x + 5 = 17
6x = 17 – 5
6x = 12
x = $\mathsf{\dfrac{12}{6}}$
x = 2
If we put x is equal to two, then 6(2) + 5 is equal to 17.
b) As this is an equation, both sides are equal, which is why there is an equal sign. In order to find y, which satisfies the right-hand side (RHS) and left-hand side (LHS) of the equation, we will do some algebraic manipulations:
3y + 15 = 21
3y = 21 –15
3y = 6
y = $\mathsf{\dfrac{6}{3}}$
y = 2
if we put x is equal to two then 6(2)+5 is equal to 17.
c) In order to find the factors x2 + 6x + 9, we have to factorize the equation, which can be done as follows:
= x2 + 6x + 9
x2 + 3x + 3x + 9
x(x + 3) + 3(x + 3)
(x + 3)2
x is equal to 3 and -3.
Example 2
Solve the following
a) Find y in equation 5y + 15 = 17.
b) Find z in equation 3z + 15 = 21
Solution
a) As this is an equation, both sides must be equal for the equation to hold true. In order to find y, which satisfies the right-hand side (RHS) and left-hand side (LHS) of the equation, we will do some algebraic manipulations:
5y + 15 = 17
5y = 17 – 15
5y = 3
y = $\mathsf{\dfrac{3}{5}}$
y = 0.6
if we put x is equal to two then 5(0.6)+15 is equal to 17.
b) As this is an equation, so both sides are equal, which is why there is an equal sign. In order to find a value for z that satisfies the right-hand side (RHS) and the left-hand side (LHS) of the equation, we will do some algebraic manipulations:
3z + 15 = 21
3z = 21 –15
3z = 6
z = $\mathsf{\dfrac{6}{3}}$
z = 2
if we put x is equal to two then 3(2)+15 is equal to 21.
All images were created using GeoGebra.
